2014COMC加拿大数学公开赛真题免费下载

历年 Canadian Open Mathematics Challenge加拿大数学公开赛

真题与答案下载

 

翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你

千千万万遍

2014 COMC真题免费下载

共计2.5小时考试时间

此套试卷由三部分题目组成

4题简答题，每题4分

4题挑战题，每题6分

4题解答题，每题10分

共计12题，满分80分

不可使用任何计算器

完整版下载链接见文末

部分真题预览：

Part A Introductory Questions:

Question A3)A positive integer m has the property that when multiplied by 12, the result is a four-digit number n of the form 20A2 for some digit A. What is the 4 digit number, n?

Question A3)Alana, Beatrix, Celine, and Deanna played 6 games of tennis together. In each game, the four of them split into two teams of two and one of the teams won the game. If Alana was on the winning team for 5 games, Beatrix for 2 games, and Celine for 1 game, for how many games was Deanna on the winning team?

Part B Challenging Questions:

Question B3)5 Xs and 4 Os are arranged in the below grid such that each number is covered by either an X or an O. There are a total of 126 different ways that the Xs and Os can be placed. Of these 126 ways, how many of them contain a line of 3 Os and no line of 3 Xs?
A line of 3 in a row can be a horizontal line, a vertical line, or one of the diagonal lines 1−5−9 or 7 − 5 − 3.

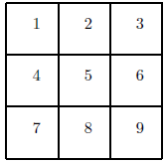
Part C Long-form Proof Problems:

Question C2)The line L given by 5y + (2m − 4)x − 10m = 0 in the xy-plane intersects the rectangle with vertices O(0, 0), A(0, 6), B(10, 6), C(10, 0) at D on the line segment OA and E on the line segment BC.

1. Show that 1 ≤ m ≤ 3.
2. Show that the area of quadrilateral ADEB is 1/3 the area of rectangle OABC.
3. Determine, in terms of m, the equation of the line parallel to L that intersects OA at F and BC at G so that the quadrilaterals ADEB, DEGF , FGCO all have the same area.

完整版真题资料可以底部二维码免费领取↓↓↓