2017COMC加拿大数学公开赛真题免费下载

历年 Canadian Open Mathematics Challenge加拿大数学公开赛

真题与答案下载

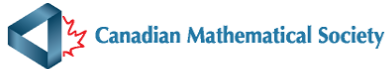
翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你

千千万万遍

2017 COMC真题免费下载

共计2.5小时考试时间

此套试卷由三部分题目组成

4题简答题，每题4分

4题挑战题，每题6分

4题解答题，每题10分

共计12题，满分80分

不可使用任何计算器

完整版下载链接见文末

部分真题预览：

Part A Introductory Questions:

Question A2)An equilateral triangle has sides of length 4cm. At each vertex, a circle with radius 2cm is drawn, as shown in the gure below. The total area of the shaded regions of the three circles is a × π cm². Determine a.

Part B Challenging Questions:

Question B1) Andrew and Beatrice practice their free throws in basketball. One day, they attempted a total of 105 free throws between them, with each person taking at least one free throw. If Andrew made exactly 1/3 of his free throw attempts and Beatrice made exactly 3/5 of her free throw attempts, what is the highest number of successful free throws they could have made between them?

Question B4)Numbers a; b and c form an arithmetic sequence if b - a = c - b. Let a, b, c be positive integers forming an arithmetic sequence with a < b < c. Let f(x) = ax² + bx + c. Two
distinct real numbers r and s satisfy f(r) = s and f(s) = r. If rs = 2017, determine the smallest possible value of a.

Part C Long-form Proof Problems:

Question C3)Let XYZ be an acute-angled triangle. Let s be the side-length of the square which has two adjacent vertices on side YZ, one vertex on side XY and one vertex on side XZ. Let h be the distance from X to the side Y Z and let b be the distance from Y to Z.

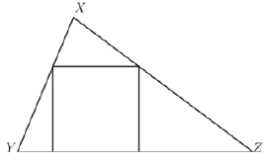
1. If the vertices have coordinates X = (2; 4), Y = (0; 0) and Z = (4; 0), find b, h and s.
2. Given the height h = 3 and s = 2, nd the base b.
3. If the area of the square is 2017, determine the minimum area of triangle XY Z.

完整版真题资料可以底部二维码免费领取↓↓↓