2013 AP Calculus BC微积分真题系列之选择题免费下载

历年AP Calculus BC微积分BC系列

真题与答案下载

翰林国际教育全网首发

力争超快速发布最全资料

助你在升学路上一帆风顺

为你的未来保驾护航

2013 AP Calculus BC Multiple Choice Practice Exam Free Download

2013 AP 微积分 BC 模拟卷选择题部分免费下载

此套Section I试卷共分两个部分组成

Part A计时55分钟，共28题

Part B计时50分钟，共17题

每道大题含有不同数量的小题

Part A需使用铅笔，无计算器

Part B可使用绘图计算器

完整版下载链接见文末

部分真题预览：

Section I，Part A，不可使用任何计算器： 4）Which of the following is an equation of the line tangent to the graph of x²-3xy = 10 at the point (1,-3)?

1. y+3= -11(x-1)
2. y+3= - (7/3)(x-1)
3. y+3= (1/3)(x-1)
4. y+3=(7/3)(x-1)
5. y+3= (11/3)(x-1)

7)A population y changes at a rate modeled by the differential equation dy/dt=0.2y(1000-y), where t is measured in years. What are all values of y for which the population is increasing at a decreasing rate?

1. 500 only
2. 0 < y < 500 only
3. 500 < y < 1000 only
4. 0 < y < 1000
5. y > 1000

9)Let y = f(x) be the solution to the differential equation dy/dx = 2x +y with initial condition f(1) = 0. What is the approximation for f(2) obtained by using Euler's method with two steps of equal length, starting at x= 1?

1. 0
2. 1
3. 2.75
4. 3
5. 6

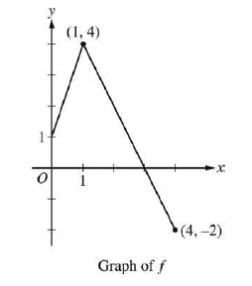18)The graph of the function f, consisting of two line segments, is shown in the figure above. Let g be the function given by g(x) = 2x+1, and let h be the function given by h(x) = f(g(x)). What is the value of h'(1)?

1. -4
2. -2
3. 4
4. 6
5. nonexistent

Section II，Part B，请使用Graphing Calculator： 76）Let f be a function whose derivative is given by f ' (x) = ln(x⁴ +5x³ +x² -7x +28). On the open interval (-4,1), at which of the following values of x does f attain a relative maximum?

1. -3.623 only
2. -0.871 only
3. -3.623 and -3.284
4. -3.459 and 0.581 only
5. -3.459,-0.871, and 0.581

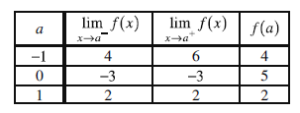77)The function f has the properties indicated in the table above. Which of the following must be true?

1. f is continuous at x = -1
2. f is continuous at x = 0
3. f is continuous at x = 1
4. f is differentiable at x = 0
5. f is differentiable at x = 1