2015PUPC普林斯顿大学物理竞赛Onsite答案免费下载

历年PUPC普林斯顿大学物理学术活动真题与答案免费下载

Onsite现场学术活动部分

翰林国际教育全网首发

力争超快速发布最全资料

为你

千千万万遍

2015PUPC普林斯顿大学物理学术活动完整版真题免费下载

Onsite现场学术活动部分此卷共4题

但每题下分不同数量的小题

完整版下载链接见文末

2015PUPC普林斯顿大学物理学术活动完整版答案免费下载

部分真题答案预览：

Question 1

a. The initial energy is

and the final energy is

For the ball not to lose contact,

Using conservation of energy, it follows that

b. A simple application of conservation of energy yields

or

Problem 2

Note that the moment of inertia of a uniformly distributed triangle with mass M and distance from center to vertex L is

a.  We apply conservation of angular momentum (about the center of the triangle), linear momentum, and energy. This gives

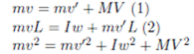
Subtracting L times (1) from (2) giveswhich we can substitute to get

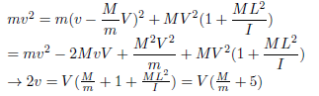
Substituting into (1) gives

Substituting into (2) gives

b. In order for a second collision to occur, we need to consider v^/ relative to V (i.e. consider the motion of the point mass in the frame of the triangle). Clearly if v^/ >V , there will be no second collision since the point mass will ’escape’ the triangle’s reach -to see this clearly, draw the circle centered at the triangle’s center (i.e. the circumcircle of the triangle). The only possible point of contact for the second collision is at the bottom of this circle so the point mass must remain stationary relative to the triangle so that the triangle can rotate and collide with the point mass a second time.

Similarly, if v^/ <V , then there will be no second collision.

If v'= V , then indeed there will be a second collision since this means the point mass remains stationary relative to the triangle while the triangle will spin with angular velocity w> 0.

Thus, a second collision occurs if V = v^/ or 2m =5m − M

M=3m

完整版真题资料可以底部二维码免费领取↓↓↓

[vc_btn title="查看更多PUPC相关详情" color="primary" align="center" i_icon_fontawesome="fa fa-globe" css_animation="zoomIn" button_block="true" add_icon="true" link="url:http%3A%2F%2Fwww.linstitute.net%2Farchives%2F26506||target:%20_blank|"]

以上就是关于【2015PUPC普林斯顿大学物理竞赛Onsite答案免费下载】的解答，如需了解学校/赛事/课程动态，可至翰林教育官网获取更多信息。

往期文章阅读推荐：

竞赛获奖≠名校offer，但拿下哈佛、MIT、牛剑Offer的学霸履历里，都有一个共同点……

【十问十答】别盲目刷竞赛！10 个核心问答，理清国际赛事规划底层逻辑！