2016PUPC普林斯顿大学物理竞赛Onsite答案免费下载

历年PUPC普林斯顿大学物理学术活动真题与答案免费下载

Onsite现场学术活动部分

翰林国际教育全网首发

力争超快速发布最全资料

为你

千千万万遍

部分真题答案预览：

Problem 1. A Jelly-Filled Universe (10 points total)

a) With no other external forces on the particle, a = 0. We can show this using Newton’s second law:

- ka = ma,

which yields a = 0. Therefore,

x = x0 + v0t.

b) Again, using Newton’s laws we have F - ka = ma, which yields a = F/(k + m). We see that the pseudo-drag force acts by contributing an effective mass to the particle. Integrating, we get

so

c) We know that the net force on the particle is constant. Defining the acceleration a0 = F/(k + m) from part b, we find

The net work done is therefore the change in kinetic energy during the time T :

d)Kinetic friction is a constant braking force, so in a given time interval t the particle experiences a decrease in speed ofv α- t. That is, the speed decreases at a constant rate. For viscous drag, the force increases linearly with speed, sov α-v t, which implies that the speed decreases exponentially fast v∼exp( -kt). Unlike the other forces, the pseudo-drag force only acts in the presence of other forces. Alone, it has no effect on the system. In the presence of other forces, it acts by increasing the effective mass of the particle to m →m + k.

e)The force of gravity is Fg = −mg, where m is the particle’s gravitational mass. Using Newton’s second law, we find

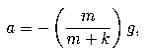
so the integrated equations give

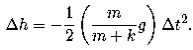
Solving for the time elapsed, we find

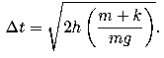
f)  It is indeed possible to replace g with an e↵ective gravitational field ge↵. Studying Newton’s second law, we see that

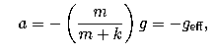
which implies that we should set

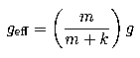
Taking the limits, we get

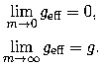
These results make sense. As m→0, the particle becomes massless, so it is no longer affected by gravity. So, it doesn’t matter whether there is a gravitational field (g ≠ 0) or not (geff= 0). In the second case, we have that the particle is infinitely massive. We no longer expect the the pseudo-force, which contributes a constant, finite term k to the effective mass, to matter. Thus, we expect geff= g, since the pseudo-drag force no longer contributes.

完整版真题资料可以底部二维码免费领取↓↓↓