- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2017 AMC 12A 真题及答案解析
2017 AMC 12A真题
答案解析请参考文末
Problem 1
Pablo buys popsicles for his friends. The store sells single popsicles for $1 each, 3-popsicle boxes for $2, and 5-popsicle boxes for $3. What is the greatest number of popsicles that Pablo can buy with $8? ![]()
Problem 2
The sum of two nonzero real numbers is 4 times their product. What is the sum of the reciprocals of the two numbers? ![]()
Problem 3
Ms. Carroll promised that anyone who got all the multiple choice questions right on the upcoming exam would receive an A on the exam. Which one of these statements necessarily follows logically? 
Problem 4
Jerry and Silvia wanted to go from the southwest corner of a square field to the northeast corner. Jerry walked due east and then due north to reach the goal, but Silvia headed northeast and reached the goal walking in a straight line. Which of the following is closest to how much shorter Silvia's trip was, compared to Jerry's trip? ![]()
Problem 5
At a gathering of ![]() people, there are
people, there are ![]() people who all know each other and
people who all know each other and ![]() people who know no one. People who know each other hug, and people who do not know each other shake hands. How many handshakes occur?
people who know no one. People who know each other hug, and people who do not know each other shake hands. How many handshakes occur? ![]()
Problem 6
Joy has ![]() thin rods, one each of every integer length from
thin rods, one each of every integer length from ![]() through
through ![]() . She places the rods with lengths
. She places the rods with lengths ![]() ,
, ![]() , and
, and ![]() on a table. She then wants to choose a fourth rod that she can put with these three to form a quadrilateral with positive area. How many of the remaining rods can she choose as the fourth rod?
on a table. She then wants to choose a fourth rod that she can put with these three to form a quadrilateral with positive area. How many of the remaining rods can she choose as the fourth rod? ![]()
Problem 7
Define a function on the positive integers recursively by ![]() ,
, ![]() if
if ![]() is even, and
is even, and ![]() if
if ![]() is odd and greater than
is odd and greater than ![]() . What is
. What is ![]() ?
? ![]()
Problem 8
The region consisting of all points in three-dimensional space within ![]() units of line segment
units of line segment ![]() has volume
has volume ![]() . What is the length
. What is the length ![]() ?
? ![]()
Problem 9
Let ![]() be the set of points
be the set of points ![]() in the coordinate plane such that two of the three quantities
in the coordinate plane such that two of the three quantities ![]() ,
, ![]() , and
, and ![]() are equal and the third of the three quantities is no greater than the common value. Which of the following is a correct description of
are equal and the third of the three quantities is no greater than the common value. Which of the following is a correct description of ![]() ?
? 
Problem 10
Chloé chooses a real number uniformly at random from the interval ![]() . Independently, Laurent chooses a real number uniformly at random from the interval
. Independently, Laurent chooses a real number uniformly at random from the interval ![]() . What is the probability that Laurent's number is greater than Chloe's number?
. What is the probability that Laurent's number is greater than Chloe's number? ![]()
Problem 11
Claire adds the degree measures of the interior angles of a convex polygon and arrives at a sum of ![]() . She then discovers that she forgot to include one angle. What is the degree measure of the forgotten angle?
. She then discovers that she forgot to include one angle. What is the degree measure of the forgotten angle? ![]()
Problem 12
There are ![]() horses, named Horse 1, Horse 2,
horses, named Horse 1, Horse 2, ![]() , Horse 10. They get their names from how many minutes it takes them to run one lap around a circular race track: Horse
, Horse 10. They get their names from how many minutes it takes them to run one lap around a circular race track: Horse ![]() runs one lap in exactly
runs one lap in exactly ![]() minutes. At time 0 all the horses are together at the starting point on the track. The horses start running in the same direction, and they keep running around the circular track at their constant speeds. The least time
minutes. At time 0 all the horses are together at the starting point on the track. The horses start running in the same direction, and they keep running around the circular track at their constant speeds. The least time ![]() , in minutes, at which all
, in minutes, at which all ![]() horses will gain simultaneously be at the starting point is
horses will gain simultaneously be at the starting point is ![]() . Let
. Let ![]() be the least time, in minutes, such that at least
be the least time, in minutes, such that at least ![]() of the horses are again at the starting point. What is the sum of the digits of
of the horses are again at the starting point. What is the sum of the digits of ![]() ?
? ![]()
Problem 13
Driving at a constant speed, Sharon usually takes ![]() minutes to drive from her house to her mother's house. One day Sharon begins the drive at her usual speed, but after driving
minutes to drive from her house to her mother's house. One day Sharon begins the drive at her usual speed, but after driving ![]() of the way, she hits a bad snowstorm and reduces her speed by
of the way, she hits a bad snowstorm and reduces her speed by ![]() miles per hour. This time the trip takes her a total of
miles per hour. This time the trip takes her a total of ![]() minutes. How many miles is the drive from Sharon's house to her mother's house?
minutes. How many miles is the drive from Sharon's house to her mother's house? ![]()
Problem 14
Alice refuses to sit next to either Bob or Carla. Derek refuses to sit next to Eric. How many ways are there for the five of them to sit in a row of ![]() chairs under these conditions?
chairs under these conditions? ![]()
Problem 15
Let ![]() , using radian measure for the variable
, using radian measure for the variable ![]() . In what interval does the smallest positive value of
. In what interval does the smallest positive value of ![]() for which
for which ![]() lie?
lie? ![]()
Problem 16
In the figure below, semicircles with centers at ![]() and
and ![]() and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter
and with radii 2 and 1, respectively, are drawn in the interior of, and sharing bases with, a semicircle with diameter ![]() . The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at
. The two smaller semicircles are externally tangent to each other and internally tangent to the largest semicircle. A circle centered at ![]() is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at
is drawn externally tangent to the two smaller semicircles and internally tangent to the largest semicircle. What is the radius of the circle centered at ![]() ?
? ![[asy] size(5cm); draw(arc((0,0),3,0,180)); draw(arc((2,0),1,0,180)); draw(arc((-1,0),2,0,180)); draw((-3,0)--(3,0)); pair P = (-1,0)+(2+6/7)*dir(36.86989); draw(circle(P,6/7)); dot((-1,0)); dot((2,0)); dot(P); [/asy]](https://latex.artofproblemsolving.com/c/7/0/c70afdd05a6954478364e08a7b13089dc5022e4a.png)
![]()
Problem 17
There are ![]() different complex numbers
different complex numbers ![]() such that
such that ![]() . For how many of these is
. For how many of these is ![]() a real number?
a real number? ![]()
Problem 18
Let ![]() equal the sum of the digits of positive integer
equal the sum of the digits of positive integer ![]() . For example,
. For example, ![]() . For a particular positive integer
. For a particular positive integer ![]() ,
, ![]() . Which of the following could be the value of
. Which of the following could be the value of ![]() ?
? ![]()
Problem 19
A square with side length ![]() is inscribed in a right triangle with sides of length
is inscribed in a right triangle with sides of length ![]() ,
, ![]() , and
, and ![]() so that one vertex of the square coincides with the right-angle vertex of the triangle. A square with side length
so that one vertex of the square coincides with the right-angle vertex of the triangle. A square with side length ![]() is inscribed in another right triangle with sides of length
is inscribed in another right triangle with sides of length ![]() ,
, ![]() , and
, and ![]() so that one side of the square lies on the hypotenuse of the triangle. What is
so that one side of the square lies on the hypotenuse of the triangle. What is ![]() ?
? ![]()
Problem 20
How many ordered pairs ![]() such that
such that ![]() is a positive real number and
is a positive real number and ![]() is an integer between
is an integer between ![]() and
and ![]() , inclusive, satisfy the equation
, inclusive, satisfy the equation ![]()
![]()
Problem 21
A set ![]() is constructed as follows. To begin,
is constructed as follows. To begin, ![]() . Repeatedly, as long as possible, if
. Repeatedly, as long as possible, if ![]() is an integer root of some polynomial
is an integer root of some polynomial ![]() for some
for some ![]() , all of whose coefficients
, all of whose coefficients ![]() are elements of
are elements of ![]() , then
, then ![]() is put into
is put into ![]() . When no more elements can be added to
. When no more elements can be added to ![]() , how many elements does
, how many elements does ![]() have?
have? ![]()
Problem 22
A square is drawn in the Cartesian coordinate plane with vertices at ![]() ,
, ![]() ,
, ![]() ,
, ![]() . A particle starts at
. A particle starts at ![]() . Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is
. Every second it moves with equal probability to one of the eight lattice points (points with integer coordinates) closest to its current position, independently of its previous moves. In other words, the probability is ![]() that the particle will move from
that the particle will move from ![]() to each of
to each of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , or
, or ![]() . The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is
. The particle will eventually hit the square for the first time, either at one of the 4 corners of the square or at one of the 12 lattice points in the interior of one of the sides of the square. The probability that it will hit at a corner rather than at an interior point of a side is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. What is
are relatively prime positive integers. What is ![]() ?
? ![]()
Problem 23
For certain real numbers ![]() ,
, ![]() , and
, and ![]() , the polynomial
, the polynomial ![]() has three distinct roots, and each root of
has three distinct roots, and each root of ![]() is also a root of the polynomial
is also a root of the polynomial ![]() What is
What is ![]() ?
? ![]()
Problem 24
Quadrilateral ![]() is inscribed in circle
is inscribed in circle ![]() and has side lengths
and has side lengths ![]() , and
, and ![]() . Let
. Let ![]() and
and ![]() be points on
be points on ![]() such that
such that ![]() and
and ![]() . Let
. Let ![]() be the intersection of line
be the intersection of line ![]() and the line through
and the line through ![]() parallel to
parallel to ![]() . Let
. Let ![]() be the intersection of line
be the intersection of line ![]() and the line through
and the line through ![]() parallel to
parallel to ![]() . Let
. Let ![]() be the point on circle
be the point on circle ![]() other than
other than ![]() that lies on line
that lies on line ![]() . What is
. What is ![]() ?
? ![]()
Problem 25
The vertices ![]() of a centrally symmetric hexagon in the complex plane are given by
of a centrally symmetric hexagon in the complex plane are given by ![]() For each
For each ![]() ,
, ![]() , an element
, an element ![]() is chosen from
is chosen from ![]() at random, independently of the other choices. Let
at random, independently of the other choices. Let ![]() be the product of the
be the product of the ![]() numbers selected. What is the probability that
numbers selected. What is the probability that ![]() ?
? ![]()
2017AMC12A详细解析
D
C
B
A
B
B
B
D
E
C
D
B
B
C
D
B
D
D
D
E
D
E
C
A
E
1.
By the greedy algorithm, we can take two 5-popsicle boxes and one 3-popsicle box with ![]() . To prove that this is optimal, consider an upper bound as follows: at the rate of
. To prove that this is optimal, consider an upper bound as follows: at the rate of ![]() per 5 popsicles, we can get
per 5 popsicles, we can get ![]() popsicles, which is less than 14.
popsicles, which is less than 14. ![]() .
.
2.
Let ![]() be our two numbers. Then
be our two numbers. Then ![]() . Thus,
. Thus, ![]() .
. ![]() .
.
3.
Taking the contrapositive of the statement "if he got all of them right, he got an A" yields "if he didn't get an A, he didn't get all of them right", yielding the answer ![]() .
.
4.
Let ![]() represent how far Jerry walked, and
represent how far Jerry walked, and ![]() represent how far Sylvia walked. Since the field is a square, and Jerry walked two sides of it, while Silvia walked the diagonal, we can simply define the side of the square field to be one, and find the distances they walked. Since Jerry walked two sides,
represent how far Sylvia walked. Since the field is a square, and Jerry walked two sides of it, while Silvia walked the diagonal, we can simply define the side of the square field to be one, and find the distances they walked. Since Jerry walked two sides, ![]() Since Silvia walked the diagonal, she walked the hypotenuse of a 45, 45, 90 triangle with leg length 1. Thus,
Since Silvia walked the diagonal, she walked the hypotenuse of a 45, 45, 90 triangle with leg length 1. Thus, ![]() We can then take
We can then take ![]()
![]() .
.
5.
Let the group of people who all know each other be ![]() , and let the group of people who know no one be
, and let the group of people who know no one be ![]() . Handshakes occur between each pair
. Handshakes occur between each pair ![]() such that
such that ![]() and
and ![]() , and between each pair of members in
, and between each pair of members in ![]() . Thus, the answer is
. Thus, the answer is 
6.
The quadrilateral cannot be a straight line. Thus, the fourth side must be longer than ![]() and shorter than
and shorter than ![]() = 25. This means Joy can use the 19 possible integer rod lengths that fall into
= 25. This means Joy can use the 19 possible integer rod lengths that fall into ![]() . However, she has already used the rods of length
. However, she has already used the rods of length ![]() cm and
cm and ![]() cm so the answer is
cm so the answer is ![]()
![]()
7.
This is a recursive function, which means the function is used to evaluate itself. To solve this, we must identify the base case, ![]() . We also know that when
. We also know that when ![]() is odd,
is odd, ![]() . Thus we know that
. Thus we know that ![]() . Thus we know that n will always be odd in the recursion of
. Thus we know that n will always be odd in the recursion of ![]() , and we add
, and we add ![]() each recursive cycle, which there are
each recursive cycle, which there are ![]() of. Thus the answer is
of. Thus the answer is ![]() , which is answer
, which is answer ![]() .
.
8.
Let the length ![]() be
be ![]() . Then, we see that the region is just the union of the cylinder with central axis
. Then, we see that the region is just the union of the cylinder with central axis ![]() and radius
and radius ![]() and the two hemispheres connected to each face of the cylinder (also with radius
and the two hemispheres connected to each face of the cylinder (also with radius ![]() ). Thus the volume is
). Thus the volume is ![]()
![]()
![]()
9.
If the two equal values are ![]() and
and ![]() , then
, then ![]() . Also,
. Also, ![]() because 3 is the common value. Solving for
because 3 is the common value. Solving for ![]() , we get
, we get ![]() . Therefore the portion of the line
. Therefore the portion of the line ![]() where
where ![]() is part of
is part of ![]() . This is a ray with an endpoint of
. This is a ray with an endpoint of ![]() .
.
Similar to the process above, we assume that the two equal values are ![]() and
and ![]() . Solving the equation
. Solving the equation ![]() then
then ![]() . Also,
. Also, ![]() because 3 is the common value. Solving for
because 3 is the common value. Solving for ![]() , we get
, we get ![]() . Therefore the portion of the line
. Therefore the portion of the line ![]() where
where ![]() is also part of
is also part of ![]() . This is another ray with the same endpoint as the above ray:
. This is another ray with the same endpoint as the above ray: ![]() .
.
If ![]() and
and ![]() are the two equal values, then
are the two equal values, then ![]() . Solving the equation for
. Solving the equation for ![]() , we get
, we get ![]() . Also
. Also ![]() because
because ![]() is one way to express the common value (using
is one way to express the common value (using ![]() as the common value works as well). Solving for
as the common value works as well). Solving for ![]() , we get
, we get ![]() . Therefore the portion of the line
. Therefore the portion of the line ![]() where
where ![]() is part of
is part of ![]() like the other two rays. The lowest possible value that can be achieved is also
like the other two rays. The lowest possible value that can be achieved is also ![]() .
.
Since ![]() is made up of three rays with common endpoint
is made up of three rays with common endpoint ![]() , the answer is
, the answer is ![]() .
.
10.
Suppose Laurent's number is in the interval ![]() . Then, by symmetry, the probability of Laurent's number being greater is
. Then, by symmetry, the probability of Laurent's number being greater is ![]() . Next, suppose Laurent's number is in the interval
. Next, suppose Laurent's number is in the interval ![]() . Then Laurent's number will be greater with probability
. Then Laurent's number will be greater with probability ![]() . Since each case is equally likely, the probability of Laurent's number being greater is
. Since each case is equally likely, the probability of Laurent's number being greater is ![]() , so the answer is C.
, so the answer is C.
11.
We know that the sum of the interior angles of the polygon is a multiple of ![]() . Note that
. Note that ![]() and
and ![]() , so the angle Claire forgot is
, so the angle Claire forgot is ![]() . Since the polygon is convex, the angle is
. Since the polygon is convex, the angle is ![]() , so the answer is
, so the answer is ![]() .
.
12.
We know that Horse ![]() will be at the starting point after
will be at the starting point after ![]() minutes if
minutes if ![]() . Thus, we are looking for the smallest
. Thus, we are looking for the smallest ![]() such that at least
such that at least ![]() of the numbers
of the numbers ![]() divide
divide ![]() . Thus,
. Thus, ![]() has at least
has at least ![]() positive integer divisors.
positive integer divisors.
We quickly see that ![]() is the smallest number with at least
is the smallest number with at least ![]() positive integer divisors, and that
positive integer divisors, and that ![]() are each numbers of horses. Thus, our answer is
are each numbers of horses. Thus, our answer is ![]() .
.
13.
Let total distance be ![]() . Her speed in miles per minute is
. Her speed in miles per minute is ![]() . Then, the distance that she drove before hitting the snowstorm is
. Then, the distance that she drove before hitting the snowstorm is ![]() . Her speed in snowstorm is reduced
. Her speed in snowstorm is reduced ![]() miles per hour, or
miles per hour, or ![]() miles per minute. Knowing it took her
miles per minute. Knowing it took her ![]() minutes in total, we create equation:
minutes in total, we create equation:![]()
![]() Solving equation, we get
Solving equation, we get ![]()
![]() .
.
14.
Alice may sit in the center chair, in an end chair, or in a next-to-end chair. Suppose she sits in the center chair. The 2nd and 4th chairs (next to her) must be occupied by Derek and Eric, in either order, leaving the end chairs for Bob and Carla in either order; this yields ![]() ways to seat the group.
ways to seat the group.
Next, suppose Alice sits in one of the end chairs. Then the chair beside her will be occupied by either Derek or Eric. The center chair must be occupied by Bob or Carla, leaving the last two people to fill the last two chairs in either order. ![]() ways to seat Alice times
ways to seat Alice times ![]() ways to fill the next chair times
ways to fill the next chair times ![]() ways to fill the center chair times
ways to fill the center chair times ![]() ways to fill the last two chairs yields
ways to fill the last two chairs yields ![]() ways to fill the chairs.
ways to fill the chairs.
Finally, suppose Alice sits in the second or fourth chair. Then the chairs next to her must be occupied by Derek and Eric in either order, and the other two chairs must be occupied by Bob and Carla in either order. This yields ![]() ways to fill the chairs.
ways to fill the chairs.
In total, there are ![]() ways to fill the chairs, so the answer is
ways to fill the chairs, so the answer is ![]() .
.
15.
We must first get an idea of what ![]() looks like:
looks like:
Between 0 and 1, ![]() starts at
starts at ![]() and increases; clearly there is no zero here.
and increases; clearly there is no zero here.
Between 1 and ![]() ,
, ![]() starts at a positive number and increases to
starts at a positive number and increases to ![]() ; there is no zero here either.
; there is no zero here either.
Between ![]() and 3,
and 3, ![]() starts at
starts at ![]() and increases to some negative number; there is no zero here either.
and increases to some negative number; there is no zero here either.
Between 3 and ![]() ,
, ![]() starts at some negative number and increases to -2; there is no zero here either.
starts at some negative number and increases to -2; there is no zero here either.
Between ![]() and
and ![]() ,
, ![]() starts at -2 and increases to
starts at -2 and increases to  . There is a zero here by the Intermediate Value Theorem. Therefore, the answer is
. There is a zero here by the Intermediate Value Theorem. Therefore, the answer is ![]() .
.
16.
Connect the centers of the tangent circles! (call the center of the large circle ![]() )
) ![[asy] size(5cm); draw(arc((0,0),3,0,180)); draw(arc((2,0),1,0,180)); draw(arc((-1,0),2,0,180)); draw((-3,0)--(3,0)); pair P = (9/7,12/7); pair A = (-1,0); pair C = (0,0); pair B = (2,0); draw(circle(P,6/7)); dot((-1,0)); dot((2,0)); dot((0,0)); dot(P); draw((-1,0)--P); draw((2,0)--P); draw((0,0)--(9/5,12/5)); label("$A$",A,SW); label("$C$",C,S); label("$B$",B,SE); label("$P$",P,N); [/asy]](http://latex.artofproblemsolving.com/d/6/d/d6d21b070a678200eab037a5542cf5b461155f6a.png) Notice that we don't even need the circles anymore; thus, draw triangle
Notice that we don't even need the circles anymore; thus, draw triangle ![]() with cevian
with cevian ![]() :
: ![[asy] size(5cm); draw((-1,0)--(2,0)); pair P = (9/7,12/7); pair A = (-1,0); pair C = (0,0); pair B = (2,0); dot((-1,0)); dot((2,0)); dot((0,0)); dot(P); draw((-1,0)--P); draw((2,0)--P); draw((0,0)--P); label("$A$",A,SW); label("$C$",C,S); label("$B$",B,SE); label("$P$",P,N); [/asy]](http://latex.artofproblemsolving.com/1/a/a/1aa17dd98346292d2b958a6c0bade6db3bdc4e9a.png) and use Stewart's Theorem:
and use Stewart's Theorem: ![]() From what we learned from the tangent circles, we have
From what we learned from the tangent circles, we have ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() is the radius of the circle centered at
is the radius of the circle centered at ![]() that we seek.
that we seek.
Thus: ![]()
![]()
![]()
![]()
![]()
17.
Note that these ![]() such that
such that ![]() are
are ![]() for integer
for integer ![]() . So
. So ![]() This is real if
This is real if ![]() is even
is even![]() . Thus, the answer is the number of even
. Thus, the answer is the number of even ![]() which is
which is ![]() .
.
18.
Note that ![]() , so
, so ![]() . So, since
. So, since ![]() , we have that
, we have that ![]() . The only one of the answer choices
. The only one of the answer choices ![]() is
is ![]() .
.
19.
Analyze the first right triangle. ![[asy] pair A,B,C; pair D, e, F; A = (0,0); B = (4,0); C = (0,3); D = (0, 12/7); e = (12/7 , 12/7); F = (12/7, 0); draw(A--B--C--cycle); draw(D--e--F); label("$x$", D/2, W); label("$A$", A, SW); label("$B$", B, SE); label("$C$", C, N); label("$D$", D, W); label("$E$", e, NE); label("$F$", F, S); [/asy]](http://latex.artofproblemsolving.com/a/2/d/a2d8d4056c8f797b4635c3aa467fd8f36bb9281c.png) Note that
Note that ![]() and
and ![]() are similar, so
are similar, so ![]() . This can be written as
. This can be written as ![]() . Solving,
. Solving, ![]() .
.
Now we analyze the second triangle. ![[asy] pair A,B,C; pair q, R, S, T; A = (0,0); B = (4,0); C = (0,3); q = (1.297, 0); R = (2.27 , 1.297); S = (0.973, 2.27); T = (0, 0.973); draw(A--B--C--cycle); draw(q--R--S--T--cycle); label("$y$", (q+R)/2, NW); label("$A'$", A, SW); label("$B'$", B, SE); label("$C'$", C, N); label("$Q$", (q-(0,0.3))); label("$R$", R, NE); label("$S$", S, NE); label("$T$", T, W); [/asy]](http://latex.artofproblemsolving.com/a/b/c/abc0a7730ccae9580fa62d17f8130c558ceec4bc.png) Similarly,
Similarly, ![]() and
and ![]() are similar, so
are similar, so ![]() , and
, and ![]() . Thus,
. Thus, ![]() . Solving for
. Solving for ![]() , we get
, we get ![]() . Thus,
. Thus, ![]() .
.
20.
By the properties of logarithms, we can rearrange the equation to read ![]() with
with ![]() . If
. If ![]() , we may divide by it and get
, we may divide by it and get ![]() , which implies
, which implies ![]() . Hence, we have
. Hence, we have ![]() possible values
possible values ![]() , namely
, namely![]() Since
Since ![]() is equivalent to
is equivalent to ![]() , each possible value
, each possible value ![]() yields exactly
yields exactly ![]() solutions
solutions ![]() , as we can assign
, as we can assign ![]() to each
to each ![]() . In total, we have
. In total, we have ![]() solutions.
solutions.
21.
At first, ![]() .
. ![[begin{tabular}{r c l c l} (10x+10) & has root & (x=-1) & so now & (S={-1,0,10}) (-x^{10}-x^9-x^8-x^7-x^6-x^5-x^4-x^3-x^2-x+10) & has root & (x=1) & so now & (S={-1,0,1,10}) (x+10) & has root & (x=-10) & so now & (S={-10,-1,0,1,10}) (x^4-x^2-x-10) & has root & (x=2) & so now & (S={-10,-1,0,1,2,10}) (x^4-x^2+x-10) & has root & (x=-2) & so now & (S={-10,-2,-1,0,1,2,10}) (2x-10) & has root & (x=5) & so now & (S={-10,-2,-1,0,1,2,5,10}) (2x+10) & has root & (x=-5) & so now & (S={-10,-5,-2,-1,0,1,2,5,10}) end{tabular}]](http://latex.artofproblemsolving.com/f/5/3/f531a7367e454681c1e46fd8e69fed9326bc18cd.png) At this point, no more elements can be added to
At this point, no more elements can be added to ![]() . To see this, let
. To see this, let  with each
with each ![]() in
in ![]() .
. ![]() is a factor of
is a factor of ![]() , and
, and ![]() is in
is in ![]() , so
, so ![]() has to be a factor of some element in
has to be a factor of some element in ![]() . There are no such integers left, so there can be no more additional elements.
. There are no such integers left, so there can be no more additional elements. ![]() has
has ![]() elements
elements ![]()
22.
We let ![]() and
and ![]() be the probability of reaching a corner before an edge when starting at an "inside corner" (e.g.
be the probability of reaching a corner before an edge when starting at an "inside corner" (e.g. ![]() ), an "inside edge" (e.g.
), an "inside edge" (e.g. ![]() ), and the middle respectively.
), and the middle respectively.
Starting in the middle, there is a ![]() chance of moving to an inside edge and a
chance of moving to an inside edge and a ![]() chance of moving to an inside corner, so
chance of moving to an inside corner, so ![]() Starting at an inside edge, there is a
Starting at an inside edge, there is a ![]() chance of moving to another inside edge, a
chance of moving to another inside edge, a ![]() chance of moving to an inside corner, a
chance of moving to an inside corner, a ![]() chance of moving into the middle, and a
chance of moving into the middle, and a ![]() chance of reaching an outside edge and stopping. Therefore,
chance of reaching an outside edge and stopping. Therefore, ![]() Starting at an inside corner, there is a
Starting at an inside corner, there is a ![]() chance of moving to an inside edge, a
chance of moving to an inside edge, a ![]() chance of moving into the middle, a
chance of moving into the middle, a ![]() chance of moving to an outside edge and stopping, and finally a
chance of moving to an outside edge and stopping, and finally a ![]() chance of reaching that elusive outside corner. This gives
chance of reaching that elusive outside corner. This gives ![]() Solving this system of equations gives
Solving this system of equations gives ![]()
![]()
![]() Since the particle starts at
Since the particle starts at ![]() it is
it is ![]() we are looking for, so the final answer is
we are looking for, so the final answer is ![]()
23.
Let ![]() and
and ![]() be the roots of
be the roots of ![]() . Let
. Let ![]() be the additional root of
be the additional root of ![]() . Then from Vieta's formulas on the quadratic term of
. Then from Vieta's formulas on the quadratic term of ![]() and the cubic term of
and the cubic term of ![]() , we obtain the following:
, we obtain the following: ![]() Thus
Thus ![]() .
.
Now applying Vieta's formulas on the constant term of ![]() , the linear term of
, the linear term of ![]() , and the linear term of
, and the linear term of ![]() , we obtain:
, we obtain:  Substituting for
Substituting for ![]() in the bottom equation and factoring the remainder of the expression, we obtain:
in the bottom equation and factoring the remainder of the expression, we obtain: ![]() It follows that
It follows that ![]() . But
. But ![]() so
so ![]() Now we can factor
Now we can factor ![]() in terms of
in terms of ![]() as
as ![]() Then
Then ![]() and
and ![]() Hence
Hence ![]() .
.
24.
Using the given ratios, note that ![]() By AA Similarity,
By AA Similarity, ![]() with a ratio of
with a ratio of ![]() and
and ![]() with a ratio of
with a ratio of ![]() , so
, so ![]() .
.
Now we find the length of ![]() . Because the quadrilateral is cyclic, we can simply use the Law of Cosines.
. Because the quadrilateral is cyclic, we can simply use the Law of Cosines.![]()
![]()
![]() By Power of a Point,
By Power of a Point, ![]() . Thus
. Thus ![]()
25.
It is possible to solve this problem using elementary counting methods. This solution proceeds by a cleaner generating function.
We note that ![]() both lie on the imaginary axis and each of the
both lie on the imaginary axis and each of the ![]() have length
have length ![]() and angle of odd multiples of
and angle of odd multiples of ![]() , i.e.
, i.e. ![]() . When we draw these 6 complex numbers out on the complex plane, we get a crystal-looking thing. Note that the total number of ways to choose 12 complex numbers is
. When we draw these 6 complex numbers out on the complex plane, we get a crystal-looking thing. Note that the total number of ways to choose 12 complex numbers is ![]() . Now we count the number of good combinations.
. Now we count the number of good combinations.
We first consider the lengths. When we multiply 12 complex numbers together, their magnitudes multiply. Suppose we have ![]() of the numbers
of the numbers ![]() ; then we must have
; then we must have ![]() . Having
. Having ![]() will take care of the length of the product; now we need to deal with the angle.
will take care of the length of the product; now we need to deal with the angle.
We require ![]() . Letting
. Letting ![]() be
be ![]() , we see that the angles we have available are
, we see that the angles we have available are ![]() , where we must choose exactly 8 angles from the set
, where we must choose exactly 8 angles from the set ![]() and exactly 4 from the set
and exactly 4 from the set ![]() . If we found a good combination where we had
. If we found a good combination where we had ![]() of each angle
of each angle ![]() , then the amount this would contribute to our count would be
, then the amount this would contribute to our count would be  . We want to add these all up. We proceed by generating functions.
. We want to add these all up. We proceed by generating functions.
Consider![]() The expansion will be of the form
The expansion will be of the form  . Note that if we reduced the powers of
. Note that if we reduced the powers of ![]() mod
mod ![]() and fished out the coefficient of
and fished out the coefficient of ![]() and plugged in
and plugged in ![]() (and then multiplied by
(and then multiplied by  ) then we would be done. Since plugging in
) then we would be done. Since plugging in ![]() doesn't affect the
doesn't affect the ![]() 's, we do that right away. The expression then becomes
's, we do that right away. The expression then becomes![]() where the last equality is true because we are taking the powers of
where the last equality is true because we are taking the powers of ![]() mod
mod ![]() . Let
. Let ![]() denote the coefficient of
denote the coefficient of ![]() in
in ![]() . Note
. Note ![]() . We use the roots of unity filter, which states
. We use the roots of unity filter, which states![]() where
where ![]() . In our case
. In our case ![]() , so we only need to find the average of the
, so we only need to find the average of the ![]() 's.
's. We plug in
We plug in ![]() and take the average to find the sum of all coefficients of
and take the average to find the sum of all coefficients of ![]() . Plugging in
. Plugging in ![]() makes all of the above zero except for
makes all of the above zero except for ![]() and
and ![]() . Averaging, we get
. Averaging, we get ![]() . Now the answer is simply
. Now the answer is simply![[frac{binom{12}{4,8}}{6^{12}}cdot 2^{14}=boxed{frac{2^2cdot 5cdot 11}{3^{10}}}.]](http://latex.artofproblemsolving.com/3/b/5/3b5a4644b2279bceb5819681dc6d647f18334a90.png)
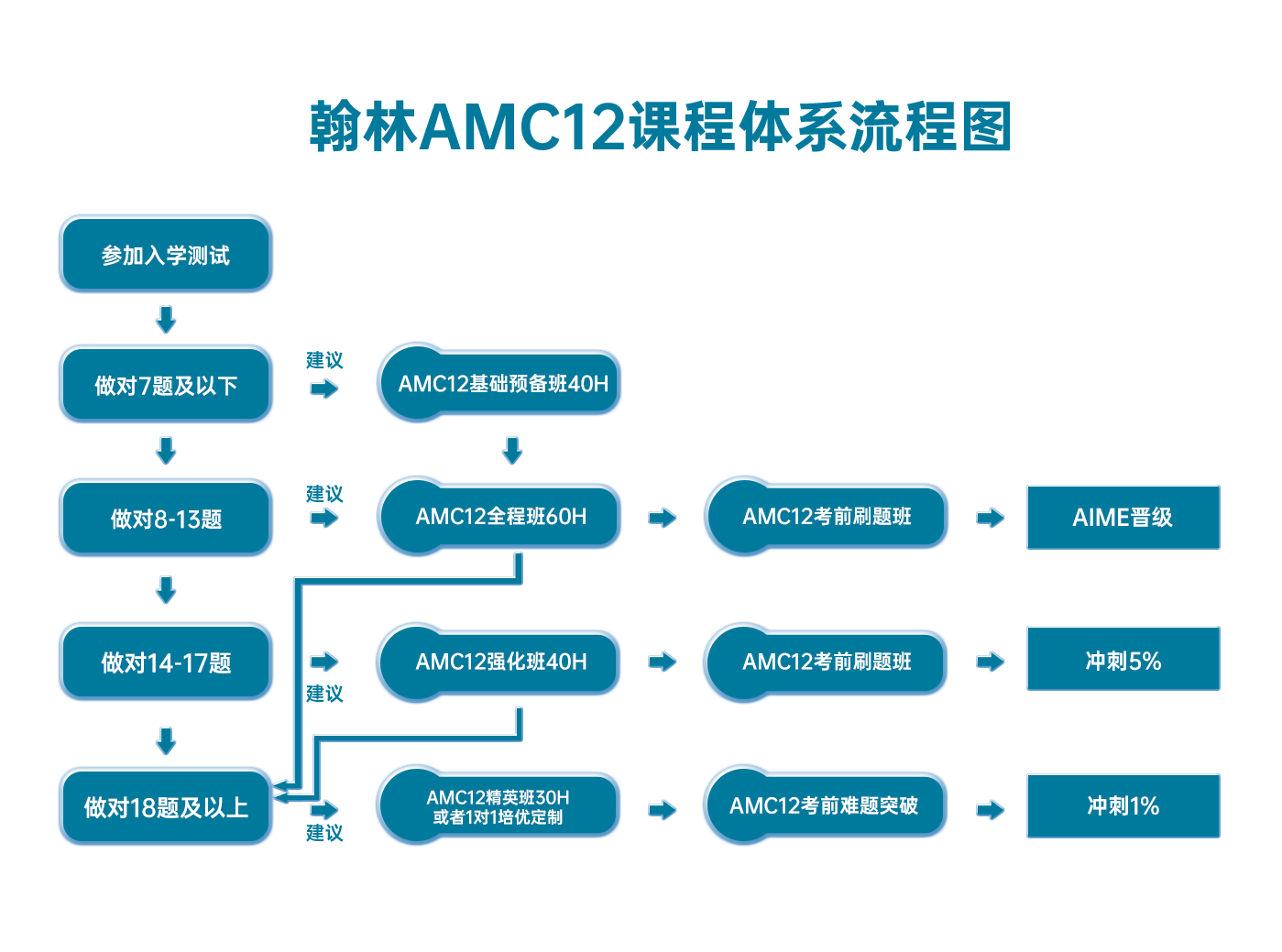
翰林AMC12课程体系流程图

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









