ap统计学难吗，ap统计学怎么学？

ap统计学难吗？根据数据显示，2020年网考时，AP统计考生人数高达18万。在AP理科中，统计考试占比仅次于微积分AB和生物。但是，对于AP统计的难度评价却不一。有些考生认为统计比微积分还难，学了半天也无法理解；而有些考生则认为统计是AP中最简单的一科，学一学就能拿到4分，稍微努力一下就能得到5分。

实际上，AP统计的难度与众不同。虽然在统计中几乎没有复杂的计算，但是其中的概念却相当复杂，需要逐级理解。重点并不在于数学解题的逻辑思维，而是如何将这些概念应用到实际问题中。因此，学生们需要花时间去理解和掌握统计中的各种概念，才能在考试中取得好成绩。

抽样 Sampling

我们常说的抽样检测就是AP统计的范围，一个抽样（Sampling），一个实验（Experiment），最后进行假设检验（Hypothesis test），这就成功完成了一个研究。这类的基础知识，是无论进行哪一个理科科目地学习都必须要具备的。所以超级重要，好好学！

简单来说，抽样（Sampling）就是从总体（population）中提出样本（sample）的过程。目的就是为了省事，不用对（量大的）总体进行一个个检测，而是通过测其中一些有代表性的样本数据再反推总体的数据。 而最简单的也是我们常说的抽样方式，就是简单随机抽样（Simple Random Sampling），从总体中随机抽取样本。那么如何做到随机，这时统计就派上用场了。1. 把总体中每个个体的数字作为标签2. 通过计算器，随机产生几个数字3. 这些选出的数字所对应的个体，就组成了我们所需要的样本。

其实，就是以数字的方式代替所有的人或物，再通过数学的方法进行随机抽取。

除了最直接的简单随机抽样，还有几种适合不同场景的抽样调查方法。比如考试经常出现的分层随机抽样（Stratifiedrandom sampling）和整群随机抽样（Cluster random sampling）。

分层随机抽样（Stratifiedrandom sampling）是先将总体按照一个标准分层，每层中抽取固定个数的个体，组成样本。这种方式的适用场景是在总体分层后，每层的差距比较大，不过层内部的个体差异不大。

比如：当校长想要知道这个高中里学生对学校的满意度，可以根据年级把所有学生分三层，每个年级是一层。再从每个年级的学生中都挑20个，最后一共有60人被抽出，也就是样本。这种时候同一年级，也就是同一层的学生差距并不大，学的知识都差不多。但是高一和高三的学生比，就相差比较多。

这是我们所说的适用于分层随机抽样的情况。

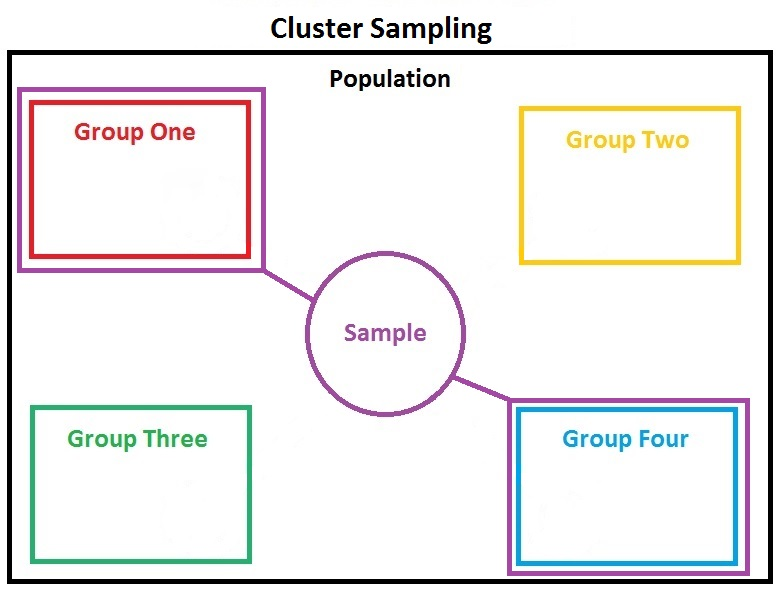
整群随机抽样（clusterrandom sampling）则是和分层随机抽样完全相反的另一种方法。是在总体分组后，随机抽取其中一或多个组的所有个体成为样本。这种方式适用于组和组之间差距不大，但是组内多样性高的情况。

比如：想要知道高三年级的同学在数学课堂上的表现，可以先根据班，把所有学生分成不同组，一个班为一组。直接抽取其中两个班，各做一次公开课就能得到结果。这时班和班的差距其实并不大（没有实验班），但是班级内部有很喜欢听课的同学，也有很不喜欢上课的同学，这会导致差异性比较大。
和分层随机抽样相比，整群随机抽样的操作难度一下子降低了，不用到处跑来跑去拜访所有层，但是大多时候很难像分层随机抽样，保证样本足够多样性。

选择合适的抽样方式，并且能通顺不出错地写出来可是超级超级超级重要的！

比如，某年真题考到量森林中树的维度：一共上百亩的森林，可以选择整群抽样，只随机测几亩森林里所有树的维度，这样肯定方便。但更好的方式则是在每一亩都挑几棵树来测维度，虽然麻烦，但是因为每一亩地的阳光，土壤资源都不一样，这样的方式保证了样本和总体更加匹配。

最后还有一种随机抽样的方法，叫做等距抽样（Systematic random sampling）。第一步不再是分组，而是要把总体中的所有个体按某种顺序排列，抽取每次的第k个作为样本。这种与众不同的方法在考试中并没有前面三种考的频繁，但也是重点之一。

举个例子：篮球队选参赛人，先按照高矮个把所有人排好顺序，从中抽取第三个，第六个，第九个，第十二个......作为样本（其实就是每次的第三个）。这种方法固然可以保证样本与总体的相似性，但也要注意避免让排列好的总体有任何的重复。如果篮球队员的排列方式是170，180，185，170，180，185... 有可能每次挑出来的篮球队员都是身高180哦。

抽样偏差 Sampling Bias

有好的抽样方法，就肯定存在有问题的方法，也就是抽样调查中出现的各种Bias。 比如从一开始就出现覆盖不全的偏差（undercoverage bias）。顾名思义，undercoverage指的是抽取样本时，并没有在应该的总体中抽取，而是漏掉了从一部分中的一个更小的总体中抽取。

比如电话抽样问题：当政府领导想要调查市民对于新政策的意向时，从电话本上随机抽取一些人的电话询问他们的意见。这看起来流程没什么问题，实际上从最开始的电话本就错了。电话本很难保证覆盖所有市民的电话，那电话没登记在电话本上该怎么办呢？这些人的意见就直接被放弃了吗？因此除非题目表示电话本上有所有人的电话，否则只要一提电话抽样，那肯定出现了undercoverage bias。

电话调查不仅有覆盖不全的偏差，同时也很容易出现其它两种偏差：不回答偏差（Nonresponsebias）和回答偏差（Response bias）。 不回答偏差（Nonresponse bias）是打了电话但对方没接，或者打通了可对方拒绝回答。只要没得到想要的答案，都算是nonresponse bias。 与之相反的回答偏差（Response bias）指的是得到了关于问题的回答，可是对方回答的并不是心里想的，或者并不是真实情况。比如打电话问道“你是否偷过东西”，一些真正偷过东西的人可能就会因为面子说没有。 这两个问题并不只会在打电话时存在，如果面对面问一些敏感问题，可能更容易出现。不过好在两个都有相应的解决办法。比如通过随机抽取更多的人，弥补上不接电话或者不回答人数的缺口，又比如通过匿名等保护信息的方式，让实验对象不受面子的影响，从而愿意说真话。

实验 vs 观察研究 

Experiment vs. Observational study

当抽样完成之后，被实验的对象也就都足够了。那如何通过一系列的操作，从实验对象中得到需要的数据，则是我们后面研究的部分。 在日常生活中简单又常见的方式，问卷调查（Survey），它其实并不能被称为一个实验，因为它只能被叫做一种观察研究（Observational study）。这类观察研究的特点，就是不对实验对象做出任何的改变。

比如：想要研究文化水平与收入之间的关系，通过问卷调查100人的文化水平与收入，得出结论。此时研究对象并没有被动的文化水平低或者高，也没有被动地挣得更多或者更少。

研究人员发了问卷，只起到了观察的作用，并没有进行实质性的改变，这种就是观察研究。 那什么才是一个真正的实验（Experiment）呢？答案有改变的实验叫做真正的实验。

举个例子：想要研究司机听不同音量的音乐和反应速度的关系，可以通过让同一个司机听两次不同大小音量的音乐，再测试反应速度进行对比。这时让司机听音乐的操作就是对他们进行的改变，也就是treatment。

是否有改变，直接影响了研究的类型，更重要的是影响了结果。观察研究因为无法确认谁导致谁，因此只能得出正相关与负相关。

如果研究结果是文化水平和收入呈正相关，也无法判定是因为文化水平高导致收入高，还是收入高所以有更好的教育资源，所以文化水平高。但是因为实验是进行了改变的，所以可以得到我们更希望的因果关系结论。

实验 Experiment

在AP统计考试中，研究比较多的是实验，因此就涉及到了实验的方法。 我们最简单常见的方法就是完全随机设计（Completely randomized design），将每一个实验对象都随机分配至实验组或对照组，最后把两组的数据进行对比。通常实验组是对实验对象进行改变，而对照组则是不进行改变。但有时因为实验比较复杂，实验组会有好几个，那么就要把实验对象随机分配到几个组中的一个，再进行对比。

稍微复杂一点的实验方法叫做随机区组设计（Randomized block design）。先根据某个标准把样本分为两组，再把每组的人分别随机分到实验组和对照组。

比如：研究人在不同商场中的消费金额，可以先把整体样本分为男女两组，再把每个男的随机分到两个不同的商场，女的也随机分到两个不同商场。这样不仅得到了两个商场的不同消费数据，还能将男女数据进行对比。

最后一个，也是最复杂的——配对实验（Matched-pairs design）。最简单的解释是，实验组与对照组的数据可以因为实验对象的原因一一对应起来。 其中一种情况，是让实验对象每个人做两件事。就比如之前讲到的让司机听两个不同音量的音乐，测反应速度。或者测学生入学前成绩和入学后成绩，得出上课有没有用的结论。这种一人做两件事的实验，是因一个人给出的两个数据一定是有联系的，但又不能把A的第一个数据和B的第二个数据联系起来，所以数据必须一一对应。 还有另一种情况，虽然不是同一个人做的，但是实验对象还是两两一对，得出的数据也是两两一对不能拆开，而且是matched-pairs的情况。比如研究情侣的消费水平，双胞胎谁会更高等等。他们往往有个不可分割的关系，也使得他们的数据牢牢绑定在一起。

写在最后

抽样检测不仅是统计中非常重要的一部分，在其它AP科目中往往也占据一席之地。因为统计本身就是多个学科的基础，连题目都涵盖了各个领域。AP统计作为一门基础学科，其难度在AP中并不能排上一二，若你感到难以应付，那你可能暂时还没有找到攻破它的套路。

免费领取AP统计学资料

暑期即将来临，提前占位国际课程辅导