- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2016 AMC 8 真题与答案解析
2016 AMC 8 真题
答案详细解析请参考文末
Problem 1
The longest professional tennis match lasted a total of 11 hours and 5 minutes. How many minutes was that?
![]()
Problem 2
In rectangle ![]() ,
, ![]() and
and ![]() . Point
. Point ![]() is the midpoint of
is the midpoint of ![]() . What is the area of
. What is the area of ![]() ?
?
![]()
Problem 3
Four students take an exam. Three of their scores are ![]() and
and ![]() . If the average of their four scores is
. If the average of their four scores is ![]() , then what is the remaining score?
, then what is the remaining score?
![]()
Problem 4
When Cheenu was a boy he could run ![]() miles in
miles in ![]() hours and
hours and ![]() minutes. As an old man he can now walk
minutes. As an old man he can now walk ![]() miles in
miles in ![]() hours. How many minutes longer does it take for him to travel a mile now compared to when he was a boy?
hours. How many minutes longer does it take for him to travel a mile now compared to when he was a boy?
![]()
Problem 5
The number ![]() is a two-digit number.
is a two-digit number.
• When ![]() is divided by
is divided by ![]() , the remainder is
, the remainder is ![]() .
.
• When ![]() is divided by
is divided by ![]() , the remainder is
, the remainder is ![]() .
.
What is the remainder when ![]() is divided by
is divided by ![]() ?
?
![]()
Problem 6
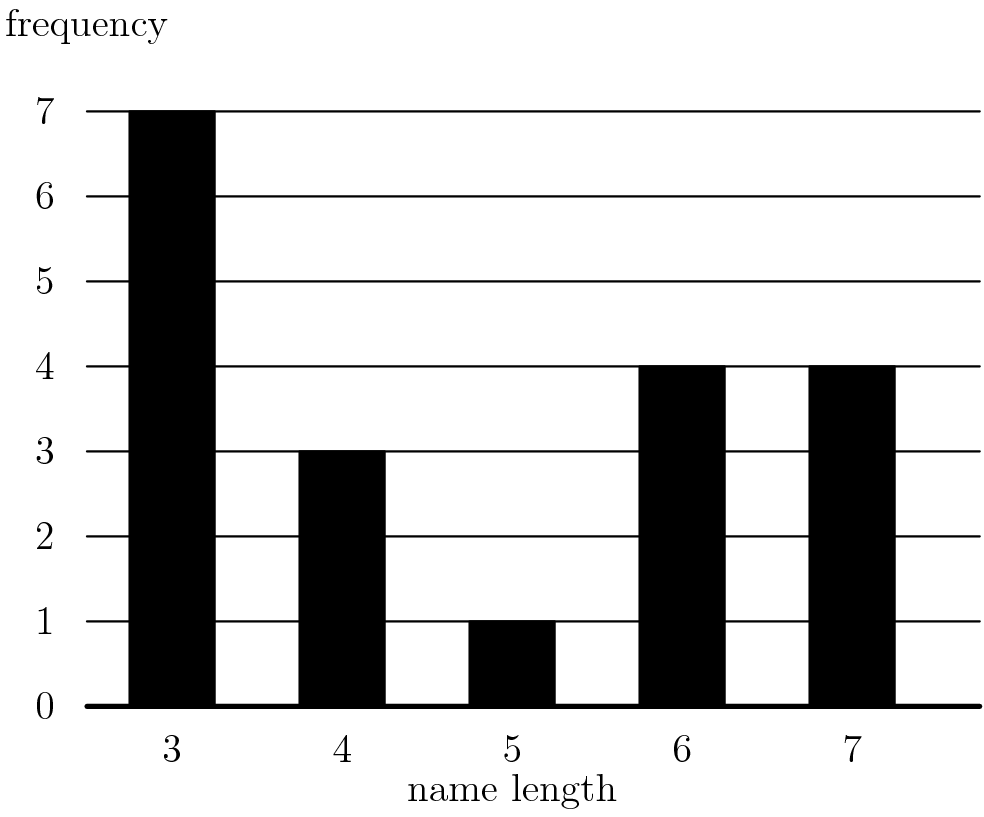
The following bar graph represents the length (in letters) of the names of 19 people. What is the median length of these names? ![]()
Problem 7
Which of the following numbers is not a perfect square?
![]()
Problem 8
Find the value of the expression![]()
![]()
Problem 9
What is the sum of the distinct prime integer divisors of ![]() ?
?
![]()
Problem 10
Suppose that ![]() means
means ![]() What is the value of
What is the value of ![]() if
if![]()
Problem 11
Determine how many two-digit numbers satisfy the following property: when the number is added to the number obtained by reversing its digits, the sum is ![]()
![]()
Problem 12
Jefferson Middle School has the same number of boys and girls. ![]() of the girls and
of the girls and ![]() of the boys went on a field trip. What fraction of the students were girls?
of the boys went on a field trip. What fraction of the students were girls?
Problem 13
Two different numbers are randomly selected from the set ![]() and multiplied together. What is the probability that the product is
and multiplied together. What is the probability that the product is ![]() ?
?
Problem 14
Karl's car uses a gallon of gas every ![]() miles, and his gas tank holds
miles, and his gas tank holds ![]() gallons when it is full. One day, Karl started with a full tank of gas, drove
gallons when it is full. One day, Karl started with a full tank of gas, drove ![]() miles, bought
miles, bought ![]() gallons of gas, and continued driving to his destination. When he arrived, his gas tank was half full. How many miles did Karl drive that day?
gallons of gas, and continued driving to his destination. When he arrived, his gas tank was half full. How many miles did Karl drive that day?
![]()
Problem 15
What is the largest power of ![]() that is a divisor of
that is a divisor of ![]() ?
?
![]()
Problem 16
Annie and Bonnie are running laps around a ![]() -meter oval track. They started together, but Annie has pulled ahead because she runs
-meter oval track. They started together, but Annie has pulled ahead because she runs ![]() faster than Bonnie. How many laps will Annie have run when she first passes Bonnie?
faster than Bonnie. How many laps will Annie have run when she first passes Bonnie?
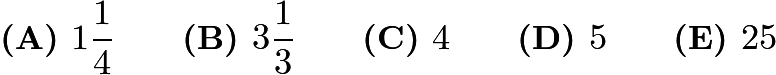
Problem 17
An ATM password at Fred's Bank is composed of four digits from ![]() to
to ![]() , with repeated digits allowable. If no password may begin with the sequence
, with repeated digits allowable. If no password may begin with the sequence ![]() then how many passwords are possible?
then how many passwords are possible?
![]()
Problem 18
In an All-Area track meet, ![]() sprinters enter a
sprinters enter a ![]() meter dash competition. The track has
meter dash competition. The track has ![]() lanes, so only
lanes, so only ![]() sprinters can compete at a time. At the end of each race, the five non-winners are eliminated, and the winner will compete again in a later race. How many races are needed to determine the champion sprinter?
sprinters can compete at a time. At the end of each race, the five non-winners are eliminated, and the winner will compete again in a later race. How many races are needed to determine the champion sprinter?
![]()
Problem 19
The sum of ![]() consecutive even integers is
consecutive even integers is ![]() . What is the largest of these
. What is the largest of these ![]() consecutive integers?
consecutive integers?
![]()
Problem 20
The least common multiple of ![]() and
and ![]() is
is ![]() , and the least common multiple of
, and the least common multiple of ![]() and
and ![]() is
is ![]() . What is the least possible value of the least common multiple of
. What is the least possible value of the least common multiple of ![]() and
and ![]() ?
?
![]()
Problem 21
A top hat contains 3 red chips and 2 green chips. Chips are drawn randomly, one at a time without replacement, until all 3 of the reds are drawn or until both green chips are drawn. What is the probability that the 3 reds are drawn?
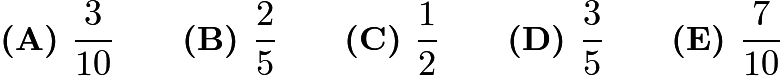
Problem 22
Rectangle ![]() below is a
below is a ![]() rectangle with
rectangle with ![]() . What is the area of the "bat wings" (shaded area)?
. What is the area of the "bat wings" (shaded area)?

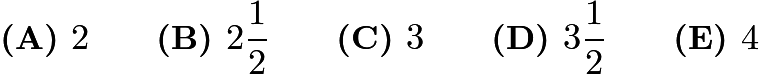
Problem 23
Two congruent circles centered at points ![]() and
and ![]() each pass through the other circle's center. The line containing both
each pass through the other circle's center. The line containing both ![]() and
and ![]() is extended to intersect the circles at points
is extended to intersect the circles at points ![]() and
and ![]() . The circles intersect at two points, one of which is
. The circles intersect at two points, one of which is ![]() . What is the degree measure of
. What is the degree measure of ![]() ?
?
![]()
Problem 24
The digits ![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() are each used once to write a five-digit number
are each used once to write a five-digit number ![]() . The three-digit number
. The three-digit number ![]() is divisible by
is divisible by ![]() , the three-digit number
, the three-digit number ![]() is divisible by
is divisible by ![]() , and the three-digit number
, and the three-digit number ![]() is divisible by
is divisible by ![]() . What is
. What is ![]() ?
?
![]()
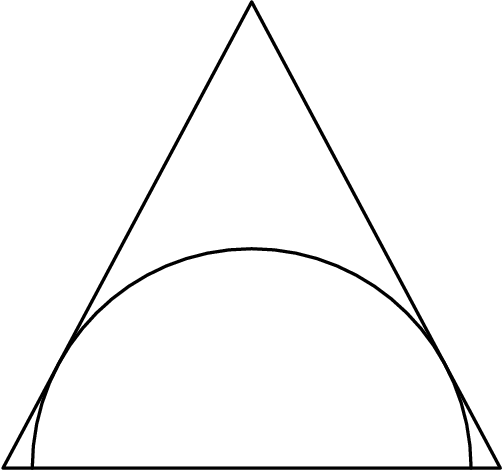
Problem 25
A semicircle is inscribed in an isosceles triangle with base ![]() and height
and height ![]() so that the diameter of the semicircle is contained in the base of the triangle as shown. What is the radius of the semicircle?
so that the diameter of the semicircle is contained in the base of the triangle as shown. What is the radius of the semicircle?
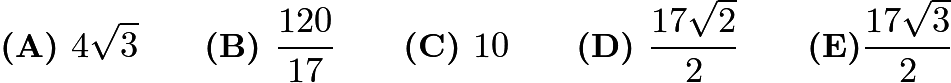
It is best to split 11 hours and 5 minutes into 2 parts, one of 11 hours and another of 5 minutes. We know that there is ![]() minutes in a hour. Therefore, there are
minutes in a hour. Therefore, there are ![]() minutes in 11 hours. Adding the second part(the 5 minutes) we get
minutes in 11 hours. Adding the second part(the 5 minutes) we get 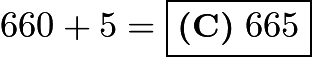 .
.
Use the triangle area formula for triangles: 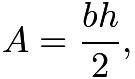 where
where ![]() is the area,
is the area, ![]() is the base, and
is the base, and ![]() is the height. This equation gives us
is the height. This equation gives us 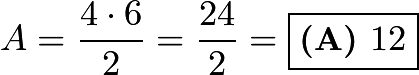 .
.
We can call the remaining score ![]() . We also know that the average, 70, is equal to
. We also know that the average, 70, is equal to 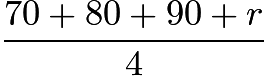 . We can use basic algebra to solve for
. We can use basic algebra to solve for ![]() :
: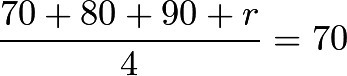
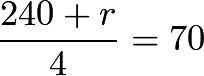
![]()
![]() giving us the answer of
giving us the answer of 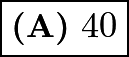 .
.
When Cheenu was a boy, he could run ![]() miles in
miles in ![]() hours and
hours and ![]() minutes
minutes ![]() minutes
minutes ![]() minutes, thus running
minutes, thus running  minutes per mile. When he is an old man, he can walk
minutes per mile. When he is an old man, he can walk ![]() miles in
miles in ![]() hours
hours ![]() minutes
minutes ![]() minutes, thus walking
minutes, thus walking 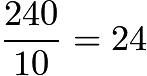 minutes per mile. Therefore it takes him
minutes per mile. Therefore it takes him  minutes longer to walk a mile now compared to when he was a boy.
minutes longer to walk a mile now compared to when he was a boy.
From the second bullet point, we know that the second digit must be ![]() . Because there is a remainder of
. Because there is a remainder of ![]() when it is divided by
when it is divided by ![]() , the multiple of
, the multiple of ![]() must end in a
must end in a ![]() . We now look for this one:
. We now look for this one: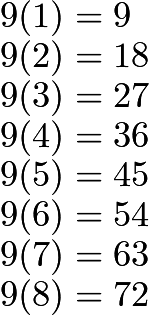 The number
The number ![]() satisfies both conditions. We subtract the biggest multiple of
satisfies both conditions. We subtract the biggest multiple of ![]() less than
less than ![]() to get the remainder. Thus,
to get the remainder. Thus, 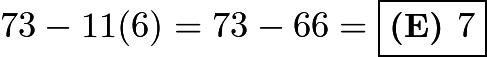 .
.
We first notice that the median name will be the ![]() name. The
name. The ![]() name is
name is 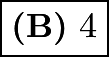 .
.
We know that our answer must have an odd exponent in order for it to not be a square. Because ![]() is a perfect square,
is a perfect square, ![]() is also a perfect square, so our answer must be
is also a perfect square, so our answer must be 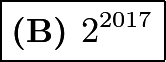 .
.
We can group each subtracting pair together:![]() After subtracting, we have:
After subtracting, we have:![]() There are
There are ![]() even numbers, therefore there are
even numbers, therefore there are 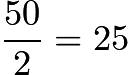 even pairs. Therefore the sum is
even pairs. Therefore the sum is 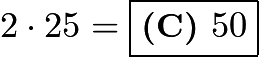
The prime factorization is ![]() . Since the problem is only asking us for the distinct prime factors, we have
. Since the problem is only asking us for the distinct prime factors, we have ![]() . Their desired sum is then
. Their desired sum is then 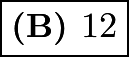 .
.
Let us plug in ![]() into
into ![]() . Thus it would be
. Thus it would be ![]() . Now we have
. Now we have ![]() . Plugging
. Plugging ![]() into
into ![]() , we have
, we have ![]() . Solving for
. Solving for ![]() we have
we have![]()

We can write the two digit number in the form of ![]() ; reverse of
; reverse of ![]() is
is ![]() . The sum of those numbers is:
. The sum of those numbers is:![]()
![]()
![]() We can use brute force to find order pairs
We can use brute force to find order pairs ![]() such that
such that ![]() . Since
. Since ![]() and
and ![]() are both digits, both
are both digits, both ![]() and
and ![]() have to be integers less than
have to be integers less than ![]() . Thus our ordered pairs are
. Thus our ordered pairs are ![]() or
or 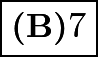 ordered pairs.
ordered pairs.
Set the number of children to a number that is divisible by two, four, and three. In this question, the number of children in the school is not a specific number because there are no actual numbers in the question, only ratios.This way, we can calculate the answer without dealing with decimals. ![]() is a number that works. There will be
is a number that works. There will be ![]() girls and
girls and ![]() boys. So, there will be
boys. So, there will be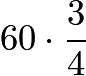 =
= ![]() girls on the trip and
girls on the trip and 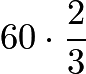 =
= ![]() boys on the trip. The total number of children on the trip is
boys on the trip. The total number of children on the trip is ![]() , so the fraction of girls on the trip is
, so the fraction of girls on the trip is ![]() or
or 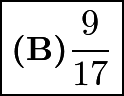
The product can only be ![]() if one of the numbers is 0. Once we chose
if one of the numbers is 0. Once we chose ![]() , there are
, there are ![]() ways we can chose the second number, or
ways we can chose the second number, or ![]() . There are
. There are 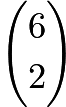 ways we can chose
ways we can chose ![]() numbers randomly, and that is
numbers randomly, and that is ![]() . So,
. So, 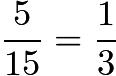 so the answer is
so the answer is 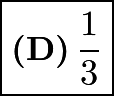 .
.
Since he uses a gallon of gas every ![]() miles, he had used
miles, he had used 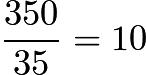 gallons after
gallons after ![]() miles. Therefore, after the first leg of his trip he had
miles. Therefore, after the first leg of his trip he had ![]() gallons of gas left. Then, he bought
gallons of gas left. Then, he bought ![]() gallons of gas, which brought him up to
gallons of gas, which brought him up to ![]() gallons of gas in his gas tank. When he arrived, he had
gallons of gas in his gas tank. When he arrived, he had 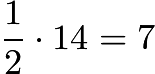 gallons of gas. So he used
gallons of gas. So he used ![]() gallons of gas on the second leg of his trip. Therefore, the second part of his trip covered
gallons of gas on the second leg of his trip. Therefore, the second part of his trip covered ![]() miles. Adding this to the
miles. Adding this to the ![]() miles, we see that he drove
miles, we see that he drove 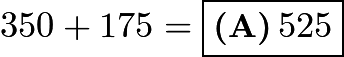 miles.
miles.
First, we use difference of squares on ![]() to get
to get ![]() . Using difference of squares again and simplifying, we get
. Using difference of squares again and simplifying, we get ![]() . Realizing that we don't need the right-hand side because it doesn't contain any factor of 2, we see that the greatest power of
. Realizing that we don't need the right-hand side because it doesn't contain any factor of 2, we see that the greatest power of ![]() that is a divisor
that is a divisor ![]() is
is  .
.
Each lap Bonnie runs, Annie runs another quarter lap, so Bonnie will run four laps before she is overtaken. This means that Annie and Bonnie are equal so that Annie needs to run another lap to overtake Bonnie. That means Annie will have run 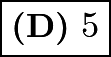 laps.
laps.
For the first three digits, there are ![]() combinations since
combinations since ![]() is not allowed. For the final digit, any of the
is not allowed. For the final digit, any of the ![]() numbers are allowed.
numbers are allowed. 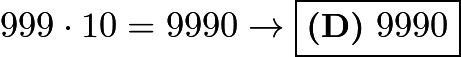
From any ![]() th race, only
th race, only ![]() will continue on. Since we wish to find the total number of races, a column representing the races over time is ideal. Starting with the first race:
will continue on. Since we wish to find the total number of races, a column representing the races over time is ideal. Starting with the first race: 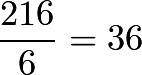
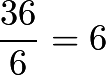
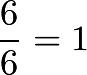 Adding all of the numbers in the second column yields
Adding all of the numbers in the second column yields 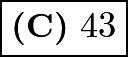
Let ![]() be the 13th consecutive even integer that's being added up. By doing this, we can see that the sum of all 25 even numbers will simplify to
be the 13th consecutive even integer that's being added up. By doing this, we can see that the sum of all 25 even numbers will simplify to ![]() since
since ![]() . Now,
. Now, ![]() Remembering that this is the 13th integer, we wish to find the 25th, which is
Remembering that this is the 13th integer, we wish to find the 25th, which is 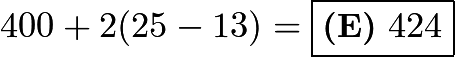 .
.
We wish to find possible values of ![]() ,
,![]() , and
, and ![]() . By finding the greatest common factor of
. By finding the greatest common factor of ![]() and
and ![]() , algebraically, it's some multiple of
, algebraically, it's some multiple of ![]() and from looking at the numbers, we are sure that it is 3, thus
and from looking at the numbers, we are sure that it is 3, thus ![]() is 3. Moving on to
is 3. Moving on to ![]() and
and ![]() , in order to minimize them, we wish to find the least such that the least common multiple of
, in order to minimize them, we wish to find the least such that the least common multiple of ![]() and
and ![]() is
is ![]() ,
, ![]() . Similarly with
. Similarly with ![]() and
and ![]() , we obtain
, we obtain ![]() . The least common multiple of
. The least common multiple of ![]() and
and ![]() is
is 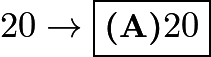
We put five chips randomly in order, and then pick the chips from the left to the right. To find the number of ways to rearrange the three red chips and two green chips, we solve for 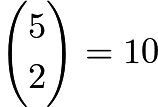 . However, we notice that whenever the last chip we draw is red, we pick both green chips before we pick the last (red) chip. Similarly, when the last chip is green, we pick all three red chips before the last (green) chip. This means that the last chip must be green in all the situations that work. This means we are left with finding the number of ways to rearrange three red chips and one green chip, which is
. However, we notice that whenever the last chip we draw is red, we pick both green chips before we pick the last (red) chip. Similarly, when the last chip is green, we pick all three red chips before the last (green) chip. This means that the last chip must be green in all the situations that work. This means we are left with finding the number of ways to rearrange three red chips and one green chip, which is 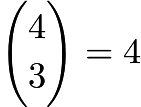 . Because a green chip will be last
. Because a green chip will be last ![]() out of the
out of the ![]() situations, our answer is
situations, our answer is 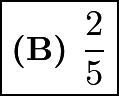 .
.
The area of trapezoid ![]() is
is 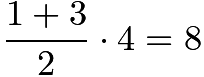 . Next, we find the height of each triangle to calculate their area. The triangles are similar, and are in a
. Next, we find the height of each triangle to calculate their area. The triangles are similar, and are in a ![]() ratio by AA similarity (alternate interior and vertical angles) so the height of the larger one is
ratio by AA similarity (alternate interior and vertical angles) so the height of the larger one is ![]() while the height of the smaller one is
while the height of the smaller one is ![]() Thus, their areas are
Thus, their areas are ![]() and
and ![]() . Subtracting these areas from the trapezoid, we get
. Subtracting these areas from the trapezoid, we get 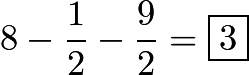 . Therefore, the answer to this problem is
. Therefore, the answer to this problem is 
Drawing the diagram[SOMEONE DRAW IT PLEASE], we see that ![]() is equilateral as each side is the radius of one of the two circles. Therefore,
is equilateral as each side is the radius of one of the two circles. Therefore, ![]() . Therefore, since it is an inscribed angle,
. Therefore, since it is an inscribed angle, 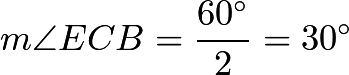 . So, in
. So, in ![]() ,
, ![]() , and
, and![]() . Our answer is
. Our answer is  .
.
We see that since ![]() is divisible by
is divisible by ![]() ,
, ![]() must equal either
must equal either ![]() or
or ![]() , but it cannot equal
, but it cannot equal ![]() , so
, so ![]() . We notice that since
. We notice that since ![]() must be even,
must be even, ![]() must be either
must be either ![]() or
or ![]() . However, when
. However, when ![]() , we see that
, we see that ![]() , which cannot happen because
, which cannot happen because ![]() and
and ![]() are already used up; so
are already used up; so![]() . This gives
. This gives ![]() , meaning
, meaning ![]() . Now, we see that
. Now, we see that ![]() could be either
could be either ![]() or
or ![]() , but
, but ![]() is not divisible by
is not divisible by ![]() , but
, but ![]() is. This means that
is. This means that ![]() and
and  .
.
Draw the altitude from the top of the triangle to its base, dividing the isosceles triangle into two right triangles with height ![]() and base
and base 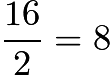 . The Pythagorean triple
. The Pythagorean triple ![]() -
-![]() -
-![]() tells us that these triangles have hypotenuses of
tells us that these triangles have hypotenuses of ![]() .Now draw an altitude of one of the smaller right triangles, starting from the foot of the first altitude we drew (which is also the center of the circle that contains the semicircle) and going to the hypotenuse of the right triangle. This segment is both an altitude of the right triangle as well as the radius of the semicircle (this is because tangent lines to circles, such as the hypotenuse touching the semicircle, are always perpendicular to the radii of the circles drawn to the point of tangency). Let this segment's length be
.Now draw an altitude of one of the smaller right triangles, starting from the foot of the first altitude we drew (which is also the center of the circle that contains the semicircle) and going to the hypotenuse of the right triangle. This segment is both an altitude of the right triangle as well as the radius of the semicircle (this is because tangent lines to circles, such as the hypotenuse touching the semicircle, are always perpendicular to the radii of the circles drawn to the point of tangency). Let this segment's length be ![]() .The area of the entire isosceles triangle is
.The area of the entire isosceles triangle is 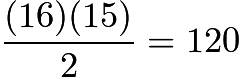 , so the area of each of the two congruent right triangles it gets split into is
, so the area of each of the two congruent right triangles it gets split into is 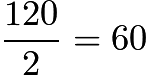 . We can also find the area of one of the two congruent right triangles by using its hypotenuse as its base and the radius of the semicircle, the altitude we drew, as its height. Then the area of the triangle is
. We can also find the area of one of the two congruent right triangles by using its hypotenuse as its base and the radius of the semicircle, the altitude we drew, as its height. Then the area of the triangle is 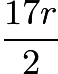 . Thus we can write the equation
. Thus we can write the equation 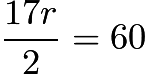 , so
, so ![]() , so
, so 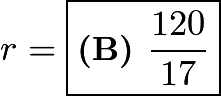 .
.


最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









