Home » 国际课程 » AP课程 » Details

AP微积分 | 精心总结AP微积分考前必看 review sheet！

Category: AP课程, 国际课程 Date: 2018年5月14日下午5:07

前言

微积分考试分为AB与BC，与AB相比，BC包含的内容更多、难度更高。考点包括极限、微分、积分（不定积分、定积分）、微分方程、级数（AB无此部分）、应用。

极限部分

这部分是微积分的基础，包含：（1）会判断极限存在或不存在，当极限存在时，如何求出该极限

（2）利用极限刻画函数的形态——渐近线（asymptote），研究函数的性质——连续性（continuous）。

1.1 极限存在的判定标准：左极限与右极限均存在且相等

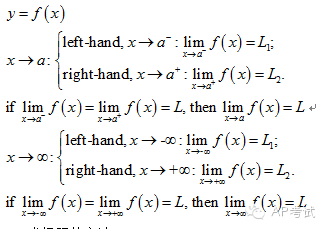
764799-ca5eaadf658b9feb0bf7e14c165ded26

1.2 求极限的方法

求a：先将a代入表达式，如果可以求出某一确定的数值，则该数值即为此函数的极限。

1.2.1 有理函数（rational function）

一般来说都是0/0或infinity/ infinity的形式，求a：通过因式分解将0因子约掉。求无穷大（infinity）：分子分母同时除以该式子的最高次项。

另外也可用L’Hopital’sRule来做。

1.2.2 洛必达法则（L’Hopital’s Rule）

具体使用时，如果所求极限是0/0或infinity/ infinity的形式，可以将分子分母两部分分别求导，再计算求完导数之后的极限。

1.2.3 等价无穷小代换

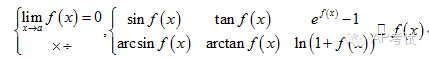
这一方法大部分国外教材与辅导书（James，Thomas，Finney，Barron）都未提及，但掌握之后会给运算带来相当大的便利。 764799-2f6cd5e82c7417f348778a541825b99e

1.2.4 幂指函数

即

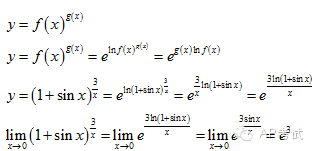这种类型的函数，做法是通过ln将其变换成指数型函数来进行运算。

1.2.5

0乘有界等于0

1.3 对于极限不存在，需要掌握左右极限不相等、无穷大和震荡三种

1.4 极限的应用

1.4.1 函数的连续性（continuity）

如果函数在某一点的极限值等于函数值，则称该函数在这一点连续。判断函数在某一点是否连续，必须要分别考察其左极限与右极限，如果左极限与右极限相等则说明极限存在，进而与该点的函数值比较，如果相等即为连续，不等即为间断。

1.4.2 间断点的类型（discontinuity）

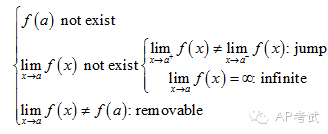
一共分为三种removable，jump，infinite 764799-ea4259dd86363692ef0083c35373d5b7

1.4.3 当函数在某一闭区间上连续时，则有三个定理

（1） The extremevalue theorem (EVT)（2） Theintermediate value theorem (IVT)（3） The zeropoint theorem (Bolzano theorem)

1.4.4 渐近线（asymptote）

分为水平（horizontal）与垂直（vertical）。其中水平的求法是分别求两个infinity的极限，如果存在则可判定有水平渐近线。垂直的求法是求某一点的极限，如果该极限等于无穷（infinity），则可判定通过在这一点存在垂直渐近线。

水平（horizontal）：

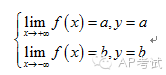
764799-ddbfba2230d9d3827fa352ee729f785d

垂直（vertical）：

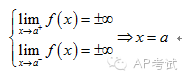
764799-919865767227d35c87cbceb348d9e1a0

导数与微分

这一部分的核心在于如何求出一个函数的导数及导数的应用。

2.1 导数与微分的定义

简单来说，导数是切线的斜率（slope），微分是切线的改变量。

2.2 求函数不同表示形式的导数

显函数，反函数，复合函数，隐函数，参数方程，极坐标

形式	求法
显函数	直接利用公式和运算法则
反函数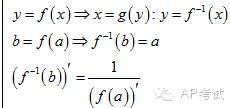
复合函数	Chain rule或微分形式不变性
隐函数	Chain rule或微分形式不变性
参数方程	微分
极坐标	微分

要注意的一点以哪个变量为基准求导数，默认是x，但也有特殊情况，如respectto sinx，则是将sinx看成一个整体进行求解。

2.2 高阶导数

它是在导数的基础之上再求一次导数，常用的是二阶导数（second derivative）

2.3 导数的直接应用

导数的直接应用是求切线和法线。求切线的时候需要注意的是所给的点是否在已知曲线上，如果在则可直接求导代数求出切线斜率（slope），如果不在则需要先设出切点，而后通过解方程的形式把切点和斜率解出来，从而得出切线。

2.4 可导与连续

在某一点可导必然连续，而连续则不一定可导。

2.5 中值定理（mean value theorem）

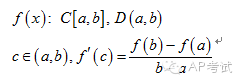从几何图形上来看，当函数在闭区间上连续、开区间内可导时，必然存在一点c使得过c点切线的斜率等于端点连线的斜率。 764799-485aa5b7fd78baac7dc6330044c00bfb

利用中值定理可以对函数进行估值和给导数估值。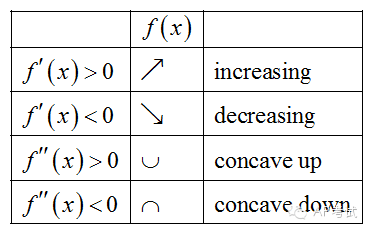

导数与微分的应用

3.1 函数与导数的关系

函数的增减性可由一阶导数的正负来判断，凹凸性可由二阶导数的正负来判断。 764799-7a4dfd1a8a252da584b522f822044578

3.2 驻点与拐点（critical and inflection point）

不同的教材对这两个点的定义不同，我们这里采用比较通用的

3.3 求函数在某一闭区间上的max and min

极值（local/relativemaximum and minimum）：邻域内最大或最小最值（global/absolutemaximum and minimum）：整个区间内最大或最小

对local来说，步骤如下：

（1）求出一阶导数等于0和不存在的点

（2）利用一阶导数是否改变符号和二阶导数的正负来判定。

对global来说，步骤如下：

（1）求出一阶导数等于0和不存在的点

（2）求出所有的函数值，最大的即为global max，最小的即为global min。

3.4 物理应用：运动

运动分为直线运动与平面运动，最原始变量为位置函数，由位置函数来定义位移（displacement）和路程（distance），在位移（displacement）的基础上定义速度（velocity）和速率（speed），在速度的基础上定义加速度（acceleration）。平面运动的位置函数用向量（vector）来表示，因此后面所有的变量都是向量的形式。直线运动的主要问题

（1）求加速与减速区间

（2）求在哪一时刻改变运动的方向

（3）求某一时间段内的路程（distance）

平面运动的主要问题

（1）速度向量、速率和加速度向量

（2）求某一时间段内的位移（displacement）和路程（distance）

3.5 相关变化率

这一部分是应用题，现实生活中的某一个量随时间变化而变化，进而求:（1）某一时刻该量的瞬时变化率（2）某一时间段内平均变化率（3）某一时间段内的累积量（积分的应用）

不定积分和定积分

4.1

与导数类似，不定积分这一部分主要是它的求法，基本的积分公式与运算必须非常熟练。（1）换元法（substitution）：将被积函数的某一部分用另外的变量代替，从而将被积函数化简，使用积分基本公式得出结果。（2）分部积分法（integral by parts）：适用于求两类不同函数乘积的积分，核心是通过交换来改变被积函数，从而将难求的变成容易求的。

（3）有理函数积分：对于分母是1次和2次的形式有固定的套路，掌握即可。

4.2 定积分

1.黎曼和（Riemann sum）使用近似逼近的方式来求面积，常用的是左端点、右端点、中点、梯形来做估计，步骤如下(1）将区间等分成n份（也可不等分）(2）按照预先设定的规则求出每一部分的面积

(3）加总。

利用黎曼和对定积分或面积进行估值，需要比较估计值和真实值的大小，可比较的是左端点、右端点和梯形三种估计方法，中点由于大小不易确定，较少出现。

黎曼积分则是在加总之后求极限，那么该极限值应该等于图形面积的真实值，也就是定积分的值（黎曼可积）。

2.求定积分的基本方法

牛顿-莱布尼茨公式，使用该公式时先求不定积分，再代入数值，因此不定积分的方法都可以在这里使用。但是需要注意的是，使用换元法的时候，变量的取值范围会发生变化。

3.求定积分的特殊方法

（1）对于某些规则图形（三角形、圆等）可用其几何意义直接算出面积，再利用定积分和面积之间的关系来求

（2）利用奇函数和偶函数的性质来求。

4.积分中值定理

求函数在某一个区间上的平均值或积分中值，使用如下公式即可。

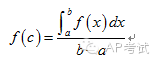
764799-246172af924f1e02b6aeaaa1730af378

5.变限积分

当被积函数确定时，积分值会随着积分区间的变化而变化，因此可将积分值看做积分区间的函数，其中需要掌握的是变限积分的求导。

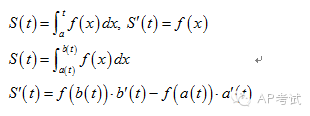
764799-1292bb508a0f9f134998808a7defdc7d
6.反常积分（improper integral）

当积分区间不是有限区间（即包含无穷大）或积分区间会使被积函数为无界的时候，求积分需要用到极限，如果极限存在，则称积分收敛（converge），不存在则称为发散（diverge）。

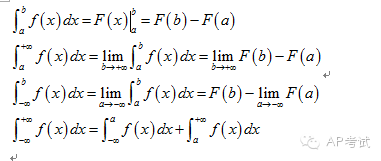
764799-8b5c06bbffdbe5074bb272157b1155f9

定积分的应用

求面积、体积、弧长

5.1 面积

求平面曲线围成的平面图形的面积，一般来说是给定一条或若干条曲线，求它与x轴、y轴或其他直线或曲线围成图形的面积。对于直角坐标系，使用定积分的几何意义来求，但需要注意的是面积永远是正数，而积分值有正有负，因此当函数大小关系或区间的边界发生变化时，要注意区别对待。

5.2 极坐标求面积

面积公式与直角坐标不同，特别需要注意的是积分的范围，如果不好判断，可用半径来反求角的范围。

5.3 体积：

求平行截面面积已知的立体图形的体积和旋转体体积，第一种图形对截面面积求积分可得体积，第二种图形有两种求法，第一种也是对截面面积求积分，不过要注意旋转截面是实心圆还是圆环，第二种是利用shell来求，掌握好展开后的圆柱壳的长宽高即可。

5.3 弧长

弧长公式用四种，一般来说在考试中如果是不允许使用计算器的部分，只会要求考生列出计算公式，不要求算出数值，而允许使用计算器的部分则可利用计算器来计算弧长的数值。

微分方程

6.1 解微分方程：

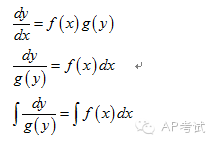
对变量可分离的微分方程，解法是将x和y分离后，等式两边同时求积分。 764799-32dcf6ee431130d53f19217e9632a316

6.2 斜率场（slope field）

根据微分方程原函数每一点切线斜率计算出来，而后将与该点切线斜率相同的线段画在坐标系中，由此所形成的图形即为斜率场。斜率场所描绘出的图形即为微分方程的解。

6.3 增长模型

分为三种：指数型增长（exponentialgrowth）有限制的增长（restrictedgrowth）逻辑斯蒂增长（logisticgrowth）

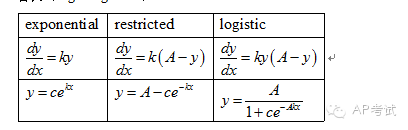
764799-46290b43b000a38fc88e68bc9bf557f0

6.4 欧拉估值（Euler’s method）

多次使用中值定理进行估值，此时c不再任取，而是固定取每一步的起始值。

级数（series）

级数共分为三部分：
无穷级数（infiniteseries）、幂级数（powerseries）、泰勒级数（Taylorseries）。

7.1 无穷级数

分为正项级数（positive）、交错级数（alternating）。这部分的核心是如何判断一个级数是收敛（converge）还是发散（diverge）。

1 正项级数（positive）

判别法有三类五种，分别是积分（integral）、比值与根值（ratio and root）、比较及极限（comparison and limit comparison）。

2 交错级数（alternating）

莱布尼茨准则（Leibniz）

收敛（converge）分为绝对收敛（absolute converge）和条件收敛（conditional converge）。

3 判定顺序

（1）将级数加绝对值取正

（2）对通项求极限，若极限不等于0，则可判定为发散，若等于0，则（2.1）利用积分（integral）、比值与根值（ratio and root）、比较及极限（comparison and limit comparison）判定，若收敛，则原级数绝对收敛，若发散，则（2.1.1）若原级数为交错级数，利用莱布尼茨准则判断，若收敛，则为条件收敛，否则为发散。

7.2 幂级数

利用比值法求出收敛半径（radius of convergence）和收敛区间（收敛域）（interval of convergence）。幂级数的性质：幂级数在收敛区间内（1）连续（2）可微（3）可积。

7.3 泰勒级数

（1）将函数展开为泰勒级数（2）求泰勒级数的和函数。

AB与BC考点对比

	AB	BC
limit	主要考察如何求limit	与AB考点相同
differentiation (derivative)	求一个给定函数的derivative	在函数的形式中，较AB多了implicit, parametric and polar function
applications of differentiation	利用derivative求函数的max min，以及解决实际问题	在motion中多了二维运动，求切线中增加了求polar形式的切线
antidifferentiation	求 antiderivative	多了 by parts 方法和求有理多项式的积分
definite integral	重点考察求定积分、Riemann sum，变限积分求导数，motion along a line	增加了求参数形式的定积分，arc length, improper integral and motion along a plane
applications of integral	求面积、体积，直线运动	求面积、体积、弧长、直线运动、平面运动
differential equation	slope field 和 growth model	增加了 Euler’s method 和 logistic growth
series	无	infinite series，power series and Taylor series