- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Statistics:复习笔记5.3.1 Sample Mean Distribution
Sample Mean Distribution
What is the distribution of the sample means?
- For any given population it can often be difficult or impractical to find the true value of the population mean, µ
- The population could be too large to collect data using a census or
- Collecting the data could compromise the individual data values and therefore taking a census could destroy the population
- Instead, the population mean can be estimated by taking the mean from a sample from within the population
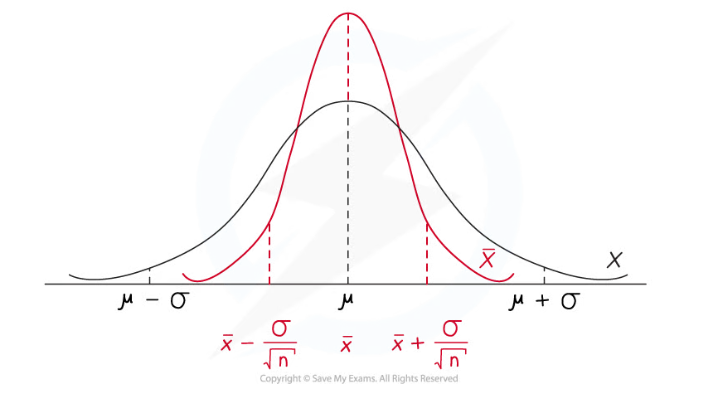
- If a sample of size n is taken from a population, X, and the mean of the sample,
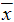 is calculated then the distribution of the sample means,
is calculated then the distribution of the sample means, 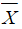 , is the distribution of all values that the sample mean could take
, is the distribution of all values that the sample mean could take - If the population, X, has a normal distribution with mean, µ , and variance,
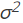 , then the mean expected value of the distribution of the sample means,
, then the mean expected value of the distribution of the sample means, 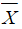 would still be µ but the variance would be reduced
would still be µ but the variance would be reduced
- Taking a mean of a sample will reduce the effect of any extreme values
- The greater the sample size, the less varied the distribution of the sample means would be
- The distribution of the means of the samples of size taken from the population, will have a normal distribution with:
- Mean,
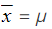
- Variance
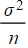
- Standard deviation
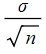
- Mean,
- For a random variable
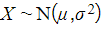 the distribution of the sample mean would be
the distribution of the sample mean would be 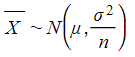
- The standard deviation of the distribution of the sample means depends on the sample size, n
- It is inversely proportional to the square root of the sample size
- This means that the greater the sample size, the smaller the value of the standard deviation and the narrower the distribution of the sample means
Worked Example
A random sample of 10 observations is taken from the population of the random variable ![]() and the sample mean is calculated as
and the sample mean is calculated as ![]() . Write down the distribution of the sample mean,
. Write down the distribution of the sample mean, ![]() .
.

Exam Tip
- Look carefully at the distribution given to determine whether the variance or the standard deviation has been given.
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1