- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Pure:复习笔记11.2.2 Problem Solving using 3D Vectors
Problem Solving using 3D Vectors
Problem-solving with 3-D vectors
- 3-D vector problems can be solved using the same principles as 2-D vector problems (see Problem Solving using Vectors)
- Vectors can be used to prove two lines are parallel, to show points are collinear (lie on the same straight line) or to find missing vertices of a given shape

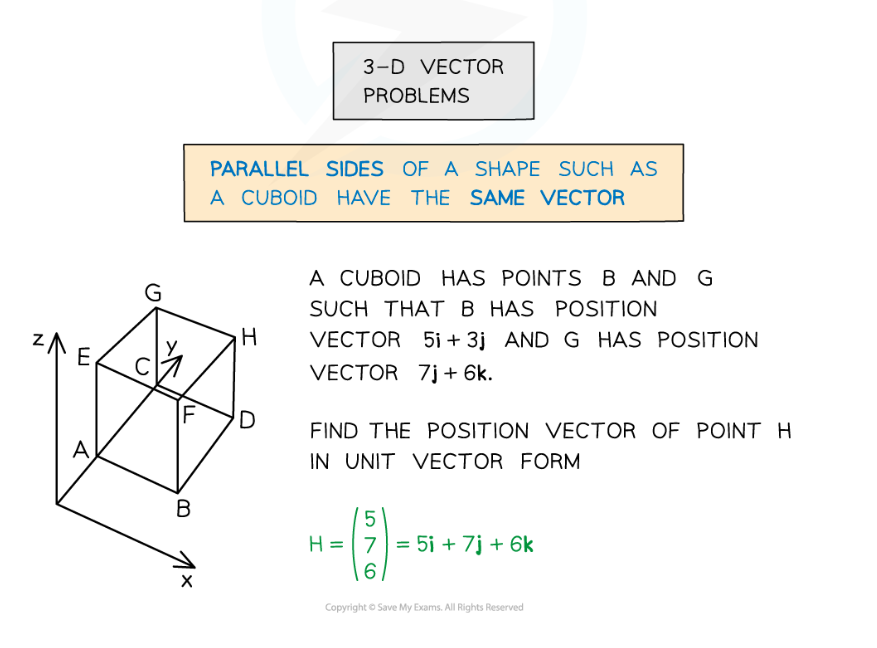
Using trig in 3-D vector problems
- 3-D vector problems can also involve using trigonometry to:
- find the angle between two vectors using Cosine Rule
- find the area of a triangle using a variation of Area Formula
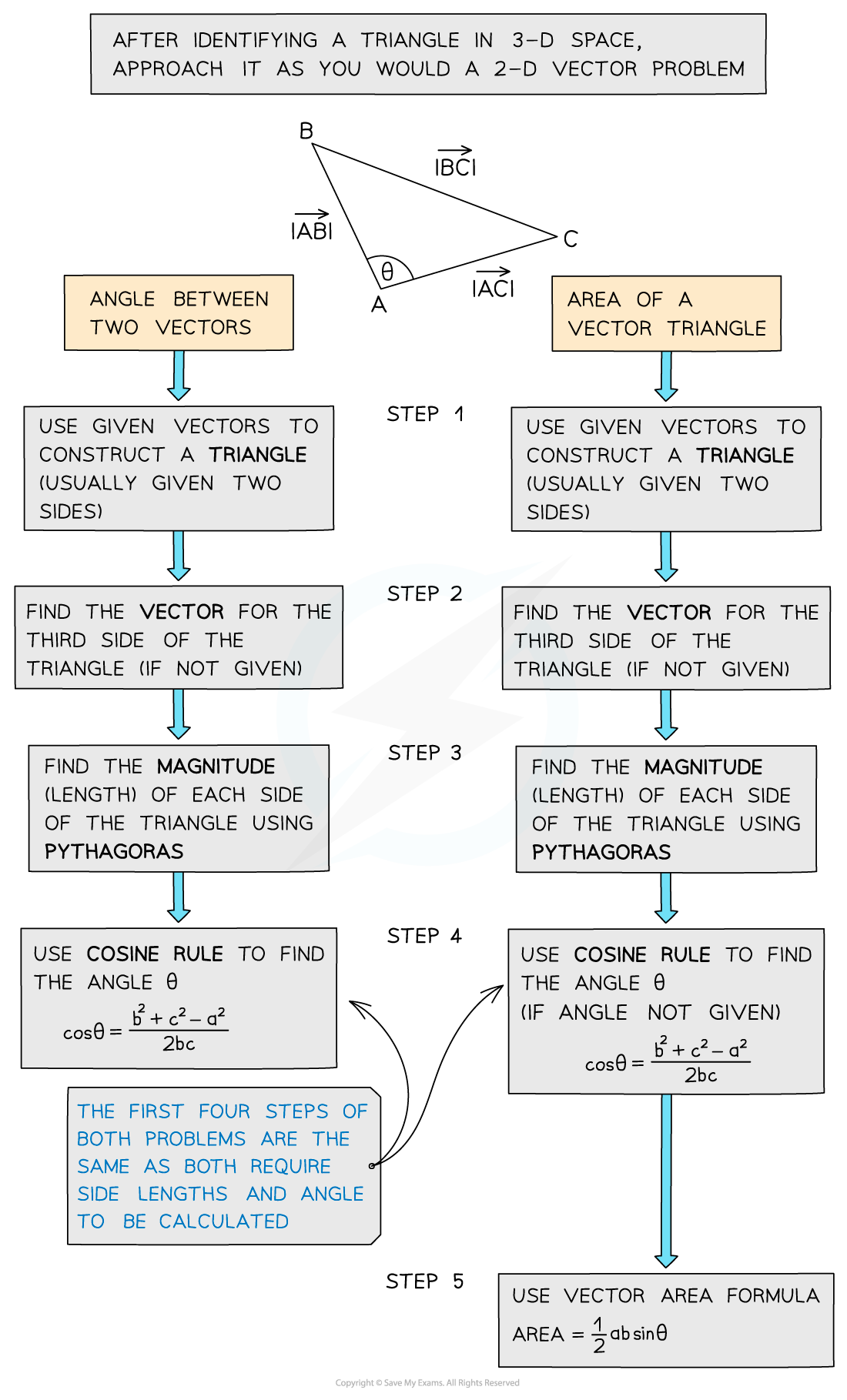
- You can find the angle between a vector and any one of the coordinate axes by using the following formulae

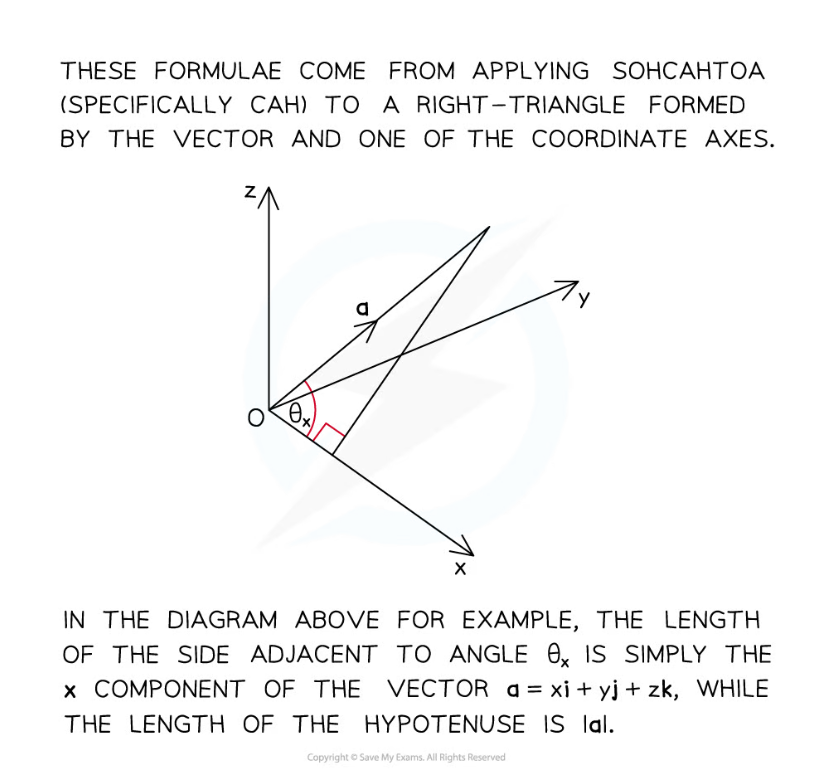
- These formulae are not in the exam formulae book
- However, they may be derived using SOHCAHTOA as shown in the diagram
- The formulae also work for vectors in two dimensions
Exam Tip
- If there is a diagram, labelling all known vectors and quantities will help, and don’t worry about trying to make your diagram 3-D, as long as you label it well.
Worked Example
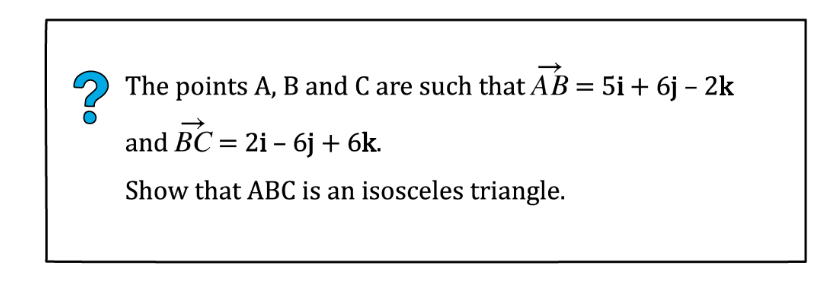
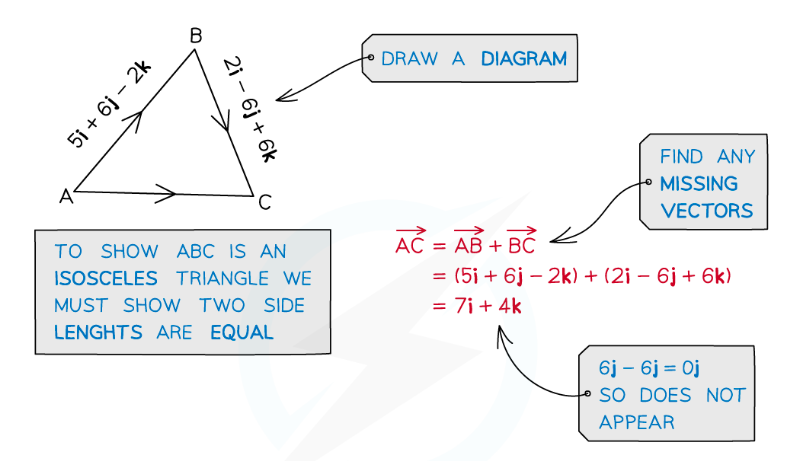
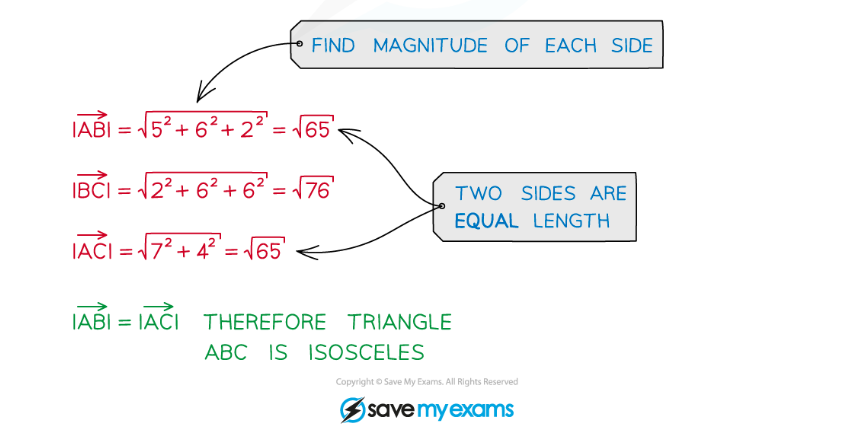
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








