Edexcel A Level Maths: Pure:复习笔记8.3.2 Particular Solutions

What is a particular solution?

• Ensure you are familiar with General Solutions first
• With extra information, the constant of integration, c, can be found
• This means the particular solution (from the family of solutions) can be found

What is a boundary condition/initial condition?

• A boundary condition is a piece of extra information that lets you find the particular solution
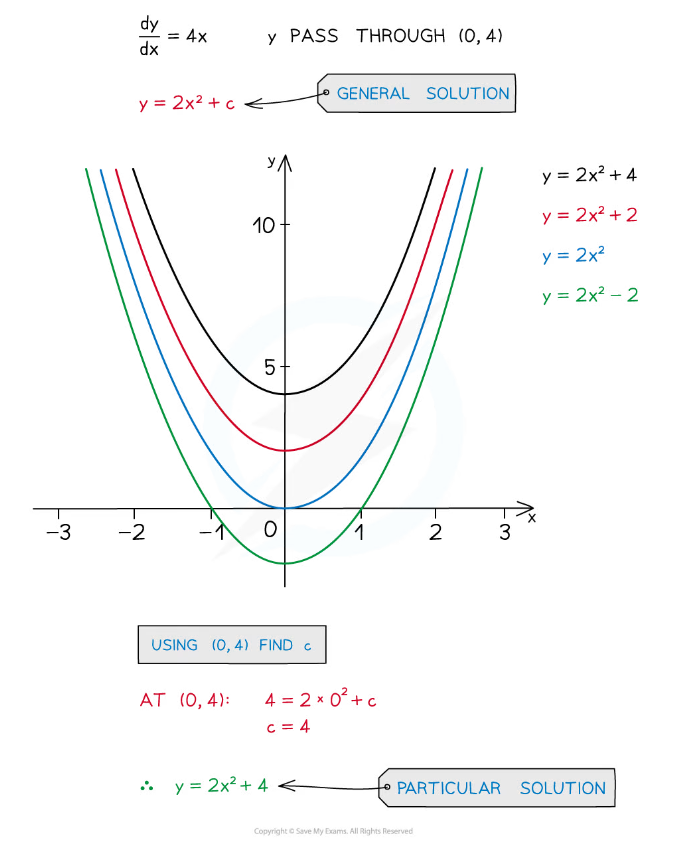
  • For example knowing y = 4 when x = 0 in the preceding example
  • In a model this could be a particle coming to rest after a certain time, ie v = 0 at time t

   

• Differential equations are used in modelling, experiments and real-life situations
• A boundary condition is often called an initial condition when it gives the situation at the start of the model or experiment
  • This is often linked to time, so t = 0

   

• It is possible to have two boundary conditions
  • eg a particle initially at rest has velocity, v = 0 and acceleration, a = 0 at time, t = 0
  • for a second order differential equation you need two boundary conditions to find the particular solution