Edexcel A Level Maths: Pure:复习笔记7.5.1 Implicit Differentiation

What is implicit differentiation?

• An equation connecting x and y is not always easy to write explicitly in the form y= f(x) or x = f(y)
• However you can still differentiate such an equation implicitly using the chain rule:

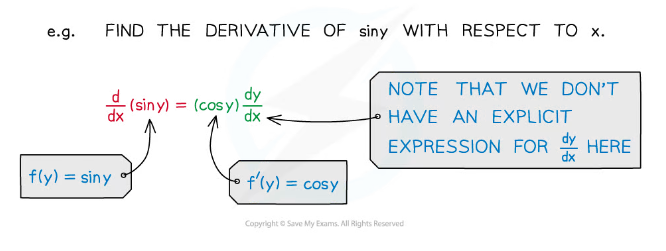
• Combining this with the product rule gives us:

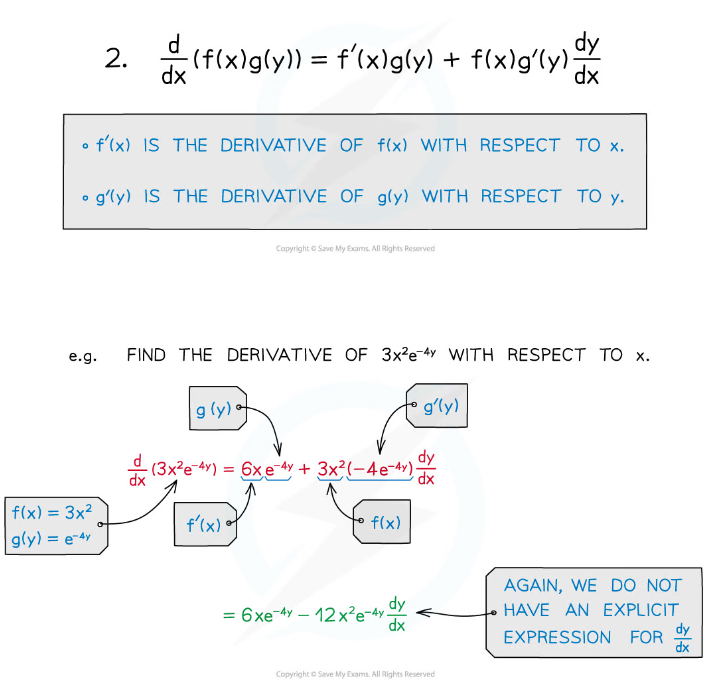
• These two special cases are especially useful:

• When x and y are connected in an equation you can differentiate both sides with respect to x and rearrange to find a formula (usually in terms of x and y ) for dy/dx
  • Note that dy/dx is a single algebraic object
  • When rearranging do not treat dy/dx as a fraction
  • Especially do not try to separate dy and dx and treat them as algebraic objects on their own!