Edexcel A Level Maths: Pure:复习笔记7.4.3 Connected Rates of Change
Connected Rates of Change
What are connected rates of change?
- In situations involving more than two variables you can use the chain rule to connect multiple rates of change into a single equation
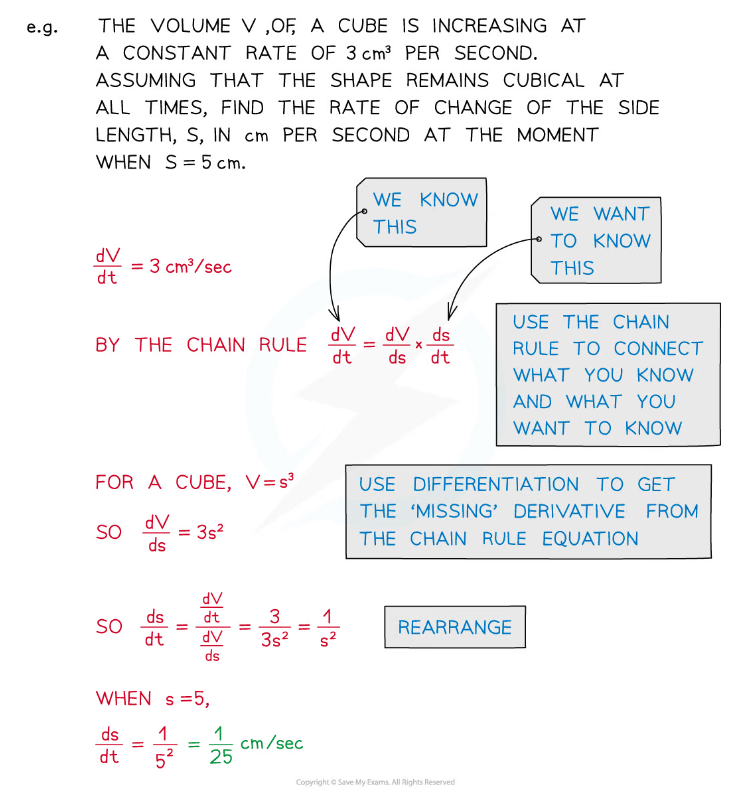
- Equations involving derivatives (ie rates of changes) are known as differential equations
- These can be solved using methods of integration (see Differential Equations )
- However setting up the equation from the information given can involve the chain rule and connected rates of change
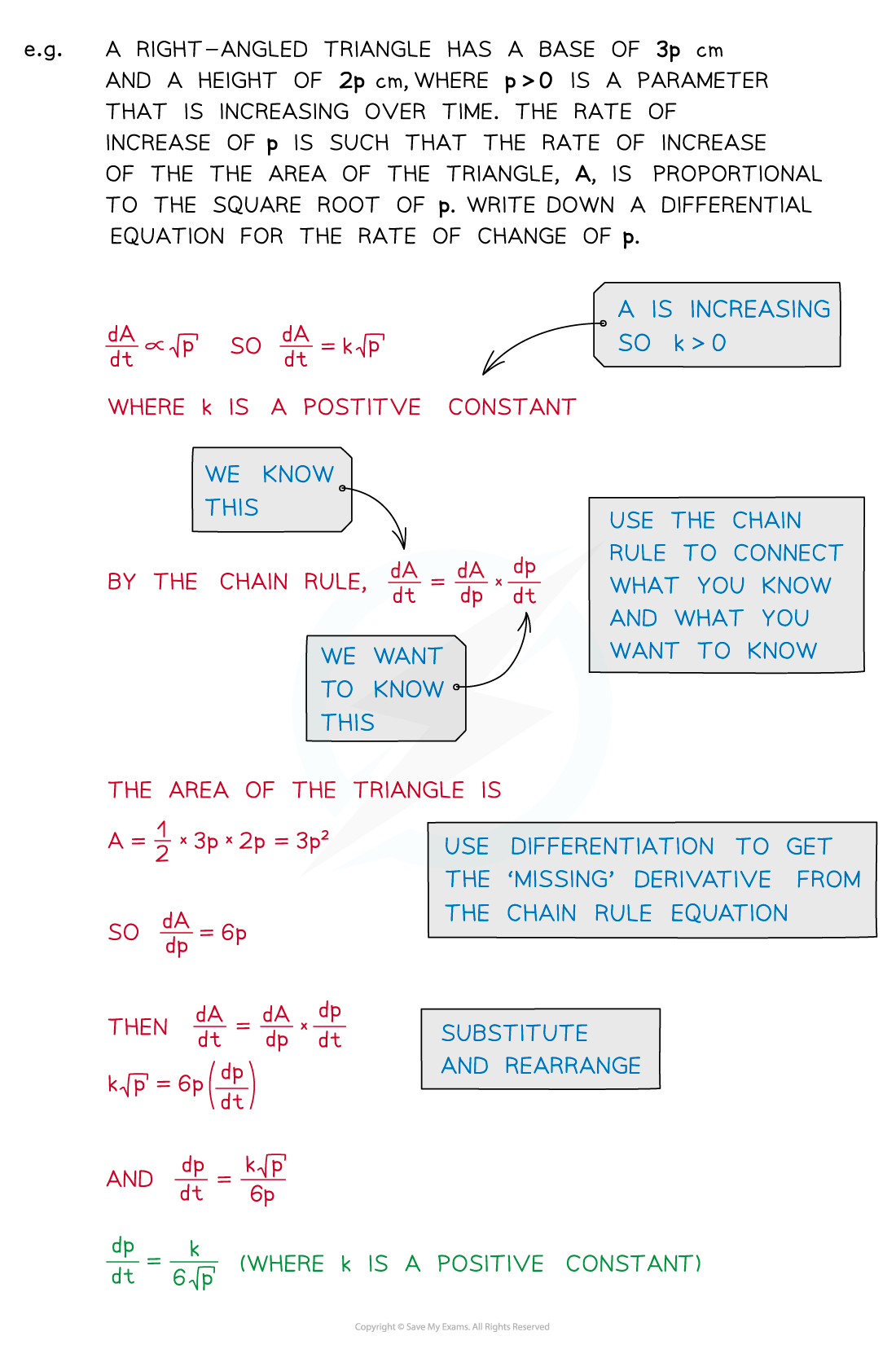
- Note from the examples above that you will often need to differentiate a formula to get one of the rates of change you need
Exam Tip
- These problems can involve a lot of letters – be sure to keep track of what they all refer to.
- Be especially sure that you are clear about which letters are variables and which are constants – these behave very differently when differentiation is involved!
Worked Example
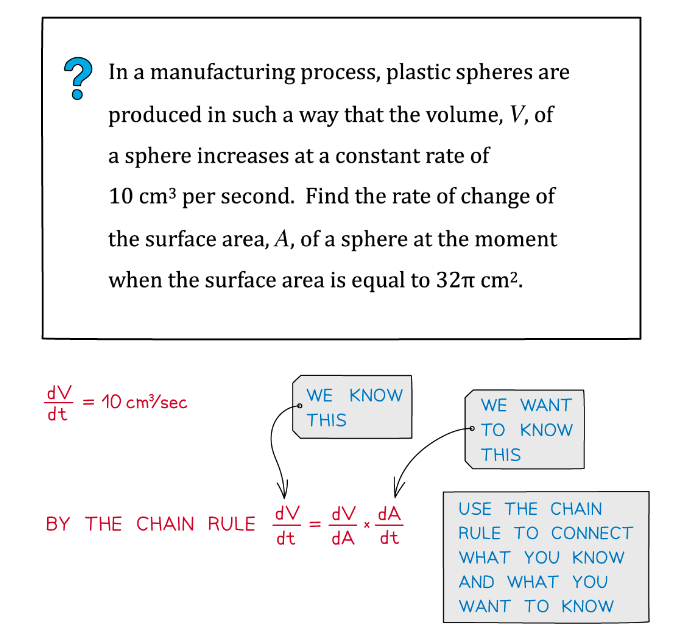
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
