- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Pure:复习笔记7.2.1 Gradients, Tangents & Normals
Gradients, Tangents & Normals
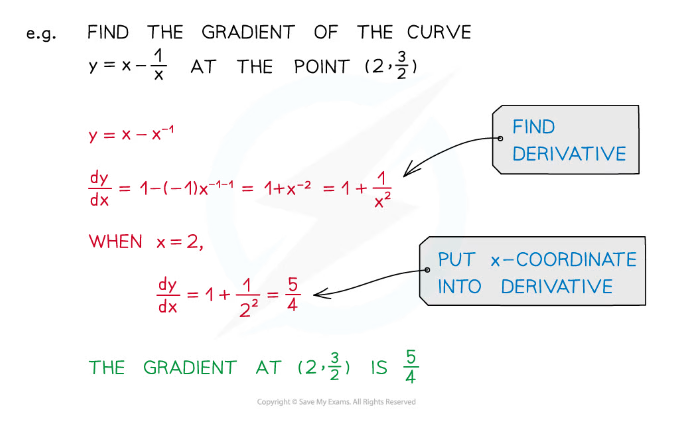
Using the derivative to find the gradient of a curve
- To find the gradient of a curve y= f(x) at any point on the curve, substitute the x‑coordinate of the point into the derivative f'(x)
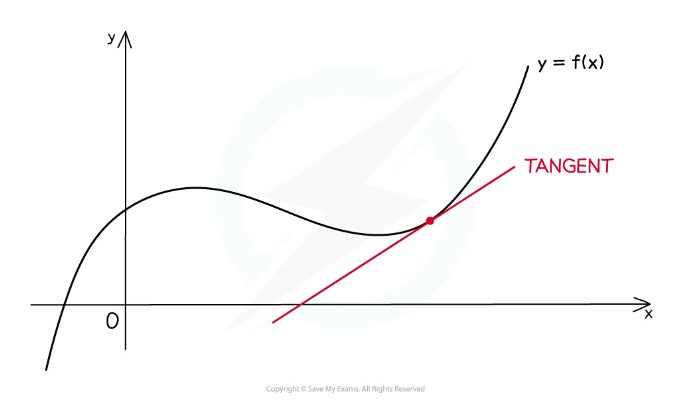
Using the derivative to find a tangent
- At any point on a curve, the tangent is the line that goes through the point and has the same gradient as the curve at that point
- For the curve y = f(x), you can find the equation of the tangent at the point (a, f(a)) using
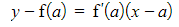
Using the derivative to find a normal
- At any point on a curve, the normal is the line that goes through the point and is perpendicular to the tangent at that point
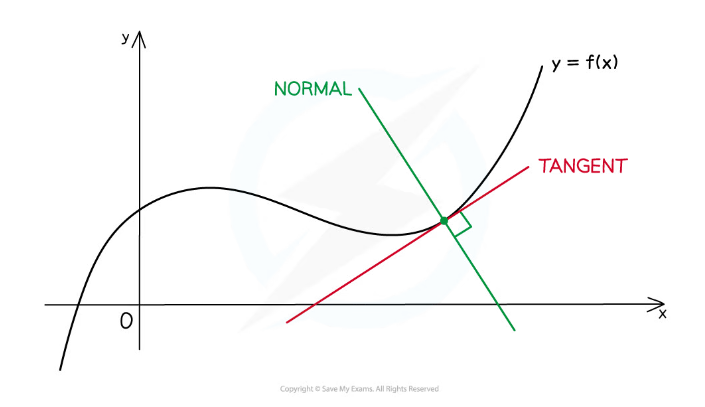
- For the curve y = f(x), you can find the equation of the normal at the point (a, f(a)) using
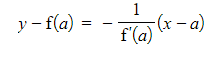
Exam Tip
- The formulae above are not in the Edexcel exam formulae booklet, but if you understand what tangents and normals are, then the formulae follow from the equation of a straight line combined with parallel and perpendicular gradients (see Worked Example below).
Worked Example


转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1