Edexcel A Level Maths: Pure:复习笔记7.1.2 First Principles Differentiation
First Principles Differentiation
What is the derivative or gradient function?
- For a curve y = f(x) there is an associated function called the derivative or gradient function
- The derivative of f(x) is written as f'(x) or
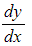
- The derivative is a formula that can be used to find the gradient of y = f(x) at any point, by substituting the x coordinate of the point into the formula
- The process of finding the derivative of a function is called differentiation
- We differentiate a function to find its derivative
What is differentiation from first principles?
- Differentiation from first principles uses the definition of the derivative of a function f(x)
- The definition is
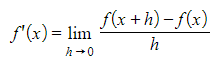
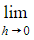means the 'limit as h tends to zero'- When
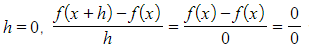which is undefined
- Instead we consider what happens as h gets closer and closer to zero
- Differentiation from first principles means using that definition to show what the derivative of a function is
How do I differentiate from first principles?
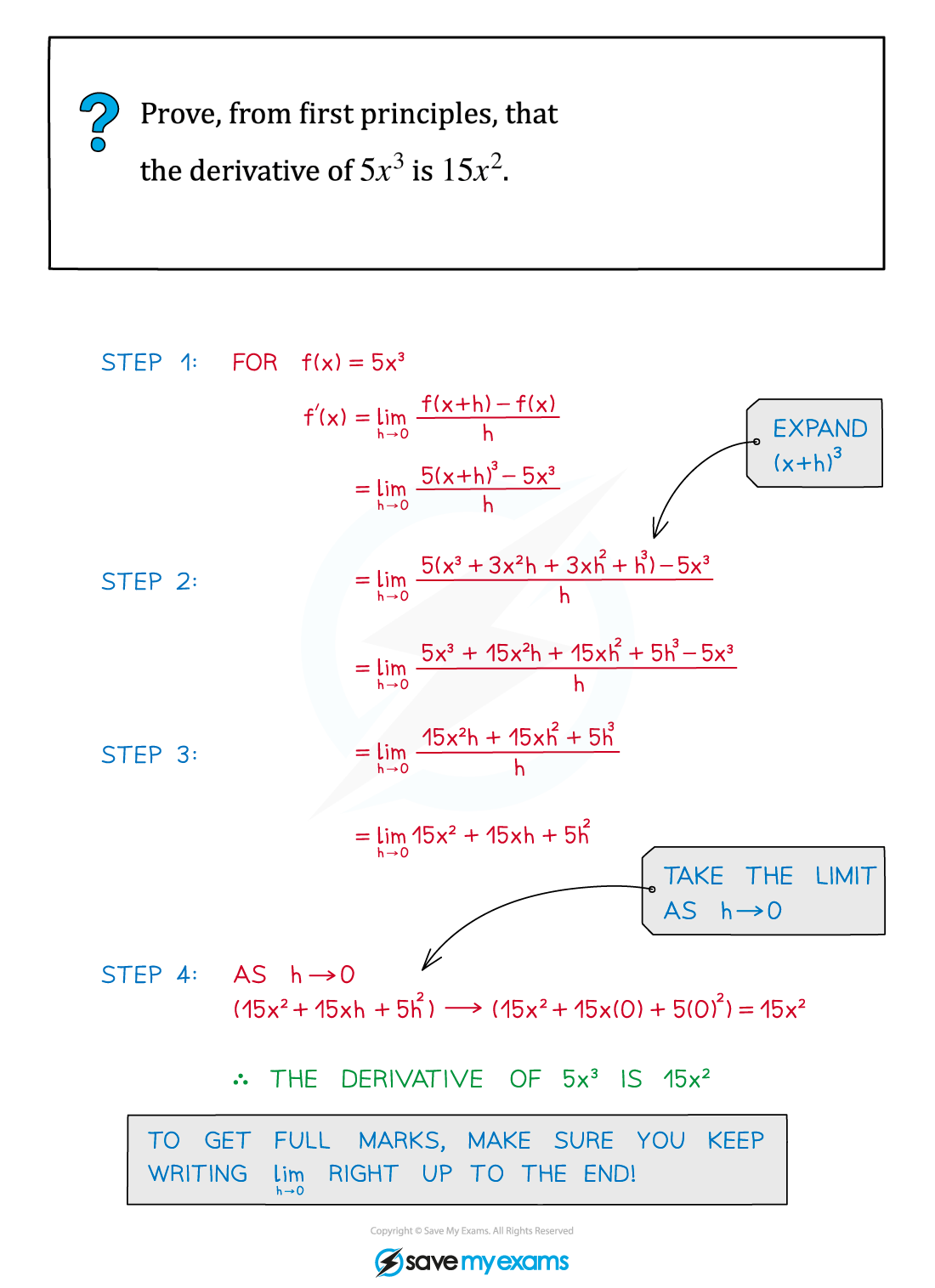
STEP 1: Identify the function f(x) and substitute this into the first principles formula
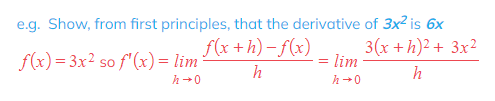
STEP 2: Expand f(x+h) in the numerator
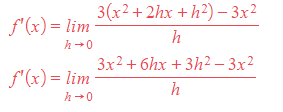
STEP 3: Simplify the numerator, factorise and cancel h with the denominator
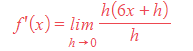
STEP 4: Evaluate the remaining expression as h tends to zero
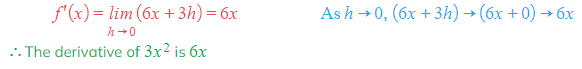
Exam Tip
- Most of the time you will not use first principles to find the derivative of a function (there are much quicker ways!). However, you can be asked on the exam to demonstrate differentiation from first principles.
- Make sure you can use first principles differentiation to find the derivatives of kx, kx2 and kx3 (where k is a constant).
Worked Example
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
