- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Pure:复习笔记5.5.2 Reciprocal Trig Functions - Graphs
What does the graph of the sec look like?
The graph of y = secx looks like this:
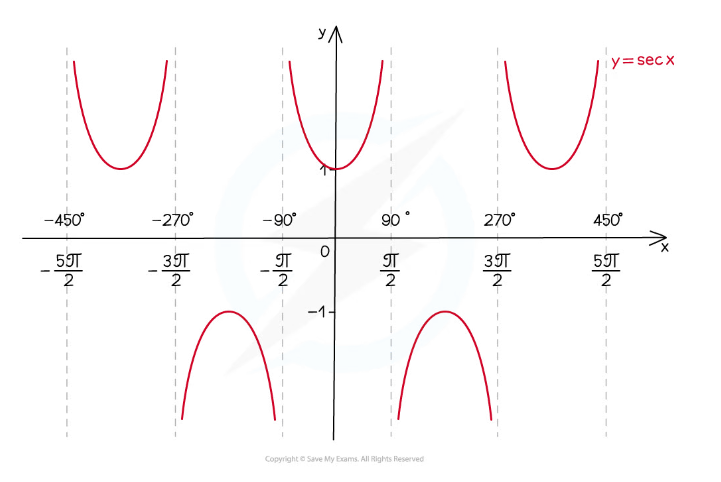
y-axis is a line of symmetry
has period (ie repeats every) 360° or 2π radians
vertical asymptotes wherever cos x= 0
domain is all x except odd multiples of 90° (90°, -90°, 270°, -270°, etc.)
the domain in radians is all x except odd multiples of π/2 (π/2, - π/2, 3π/2, -3π/2, etc.)
range is y ≤ -1 or y ≥ 1
What does the graph of the cosec look like?
The graph of y = cosec x looks like this:
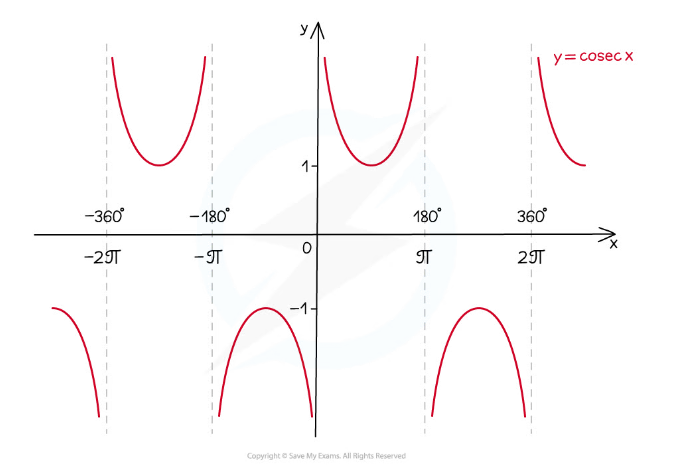
has period (ie repeats every) 360° or 2π radians
vertical asymptotes wherever sin x= 0
domain is all x except multiples of 180° (0°, 180°, -180°, 360°, -360°, etc.)
the domain in radians is all x except multiples of π (0, π, - π, 2π, -2π, etc.)
range is y ≤ -1 or y ≥ 1
What does the graph of the cot look like?
The graph of y = cot x looks like this:
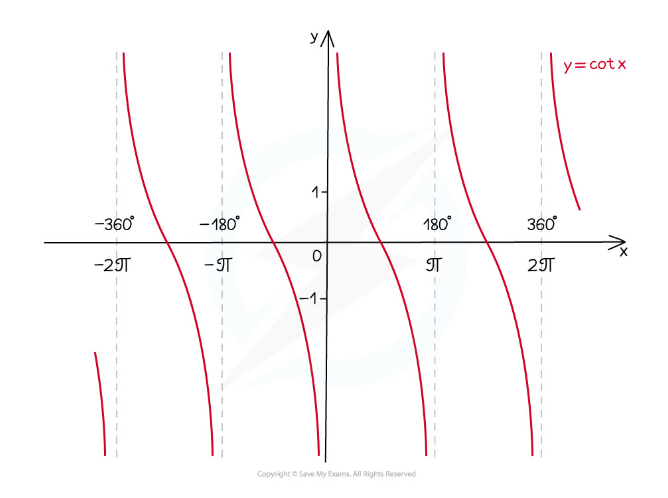
has period (ie repeats every) 180° or π radians
vertical asymptotes wherever tan x= 0
domain is all x except multiples of 180° (0°, 180°, -180°, 360°, -360°, etc.)
the domain in radians is all x except multiples of π (0, π, - π, 2π, -2π, etc.)
range is y ∈ ℝ (ie cot can take any real number value)
Make sure you know the shapes of the graphs for cos, sin and tan.
The shapes of the reciprocal trig function graphs follow from those graphs plus the definitions sec = 1/cos, cosec = 1/sin and cot = 1/tan

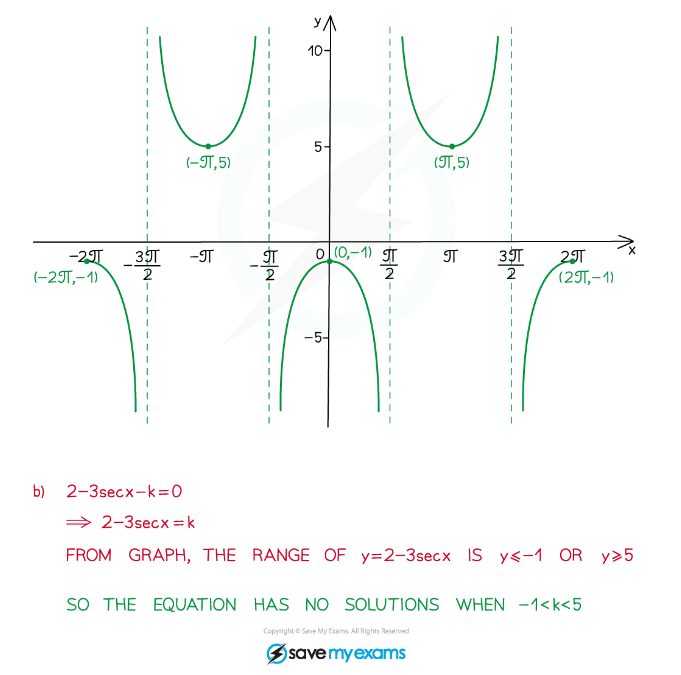
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









