Edexcel A Level Maths: Pure:复习笔记5.3.3 Quadratic Trigonometric Equations
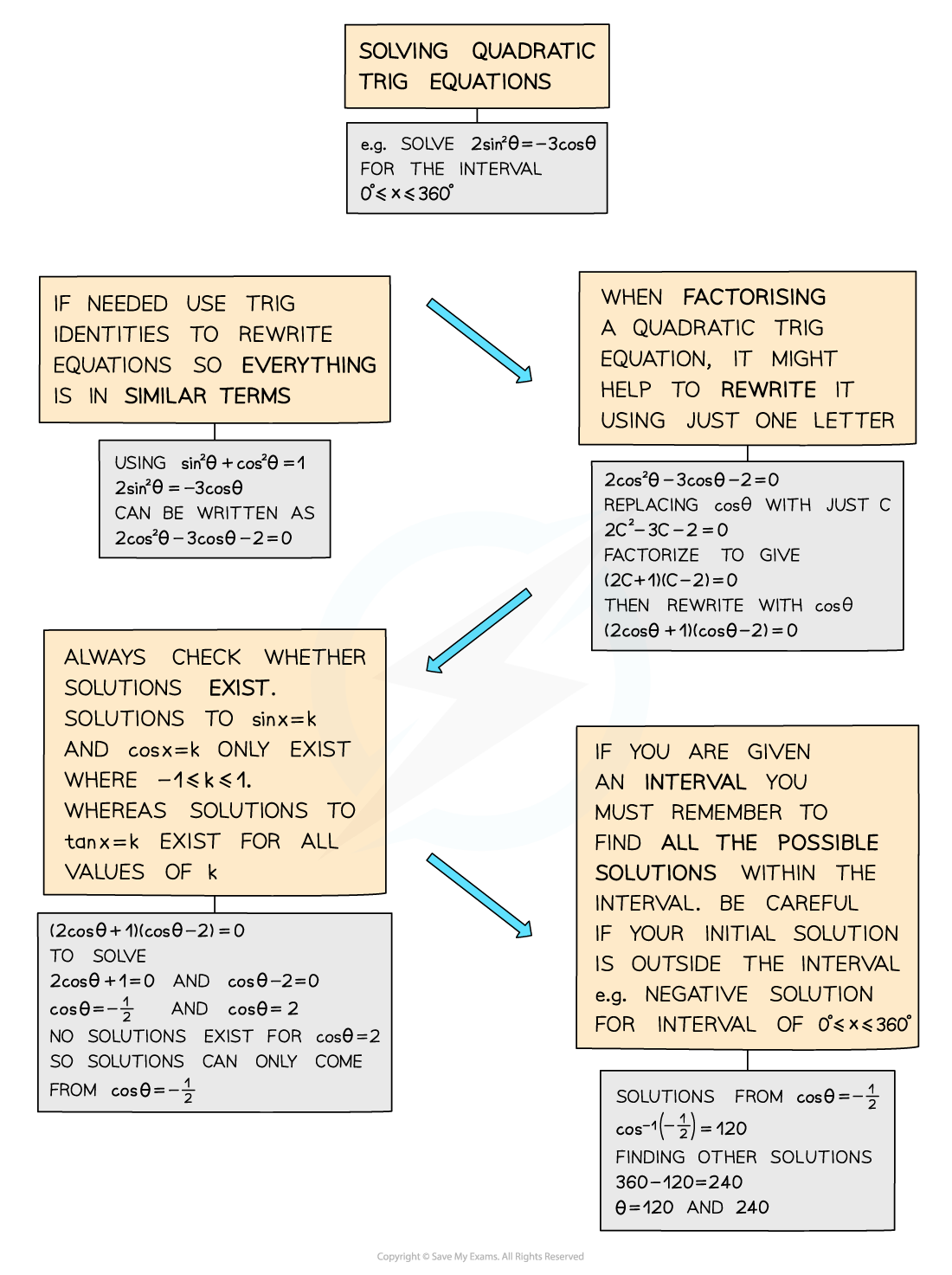
Quadratic Trigonometric Equations
Solving quadratic trigonometric equations
- If an equation involves sin2θ or cos2θ then it is a quadratic trigonometric equation
- These can be solved by factorising and/or using trigonometric identities (see Trigonometry – Simple Identities)
- As a quadratic can result in two solutions, will need to consider whether each solution exists and then find all solutions within a given interval for each
Exam Tip
- Sketch the appropriate sin, cos, tan graph to ensure you find ALL solutions within the given interval, and be super-careful if you get a negative solution but have a positive interval.
- For example, for an equation, in the interval 0° ≤ x ≤ 360°, with solution sin x = ‑¼ then sin‑1(‑¼) = -14.5 (to 1d.p.), which is not between 0 and 360 – by sketching the graph you’ll be able to spot the two solutions will be 180 + 14.5 and 360 ‑ 14.5.
Worked Example
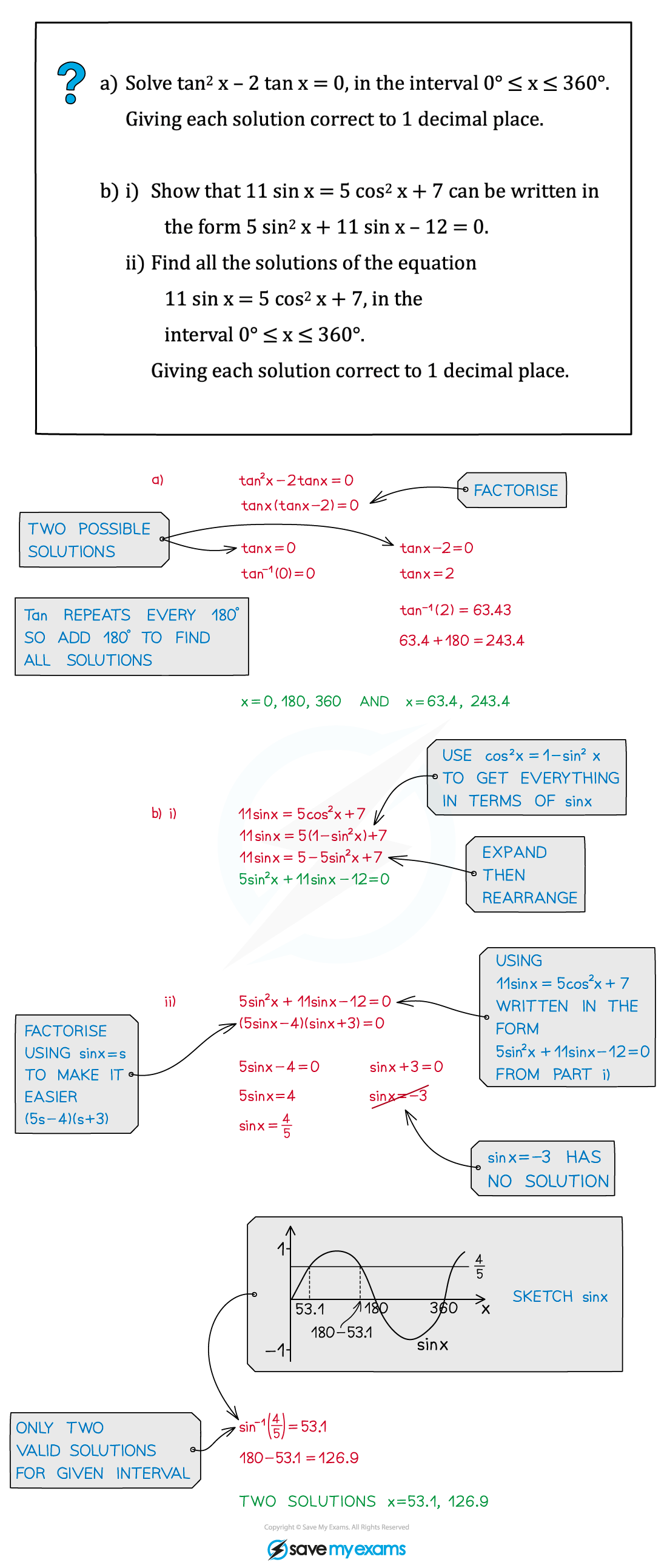
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
