- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Maths: Pure:复习笔记2.10.1 Combinations of Transformations
Combinations of Transformations
What are combinations of graph transformations?
- When you alter a function in certain ways, the effects on the graph of the function can be described by geometrical transformations
- In additional to single transformations, you need to be able to interpret the effects of multiple transformations applied to the same function
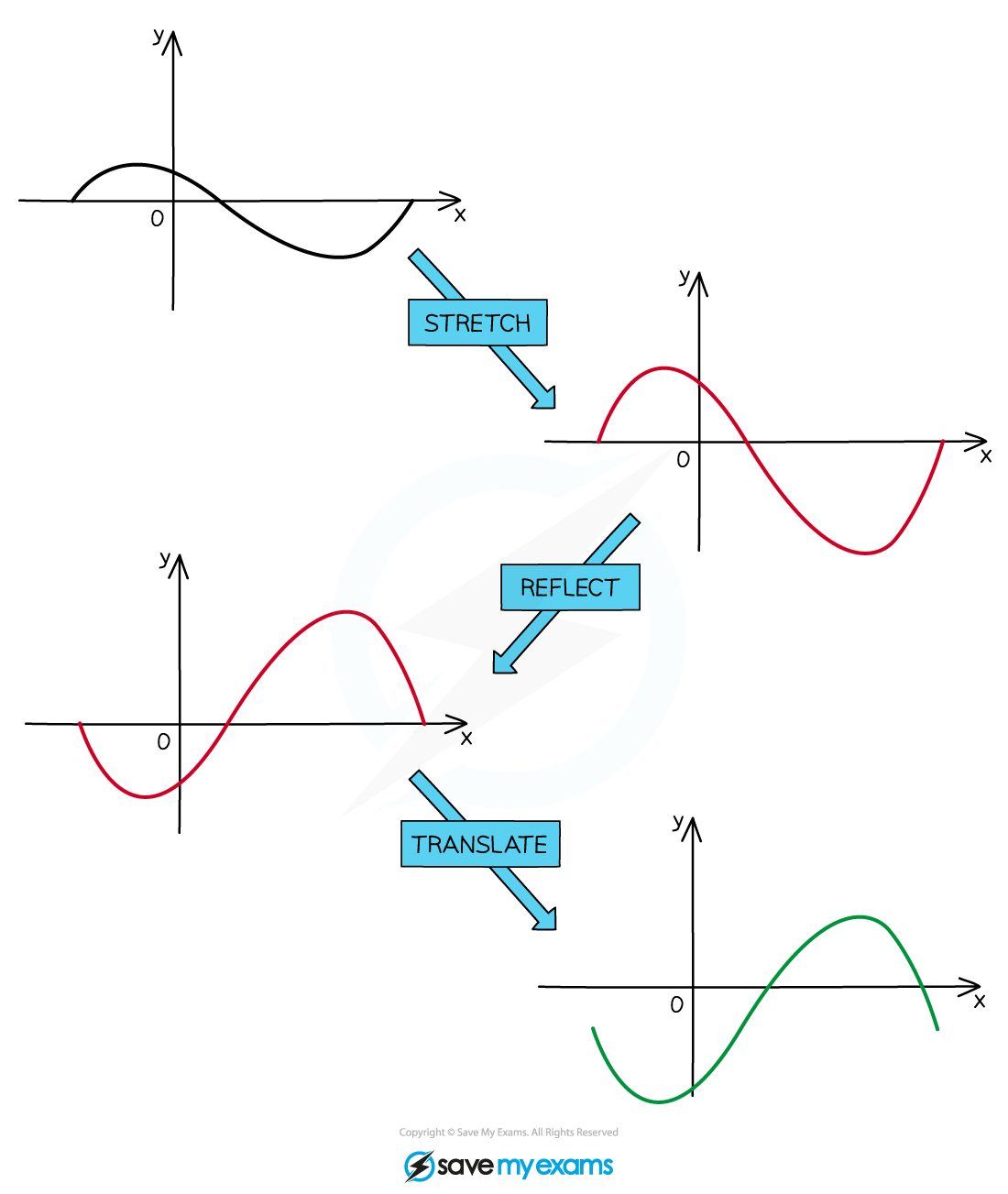
How do I combine two or more graph transformations?
- Make sure you understand the effects of individual translations, stretches, and reflections on the graph of a function (see the previous pages)
- When applying combinations of these transformations, apply them to the graph one at a time according to the following guidelines:
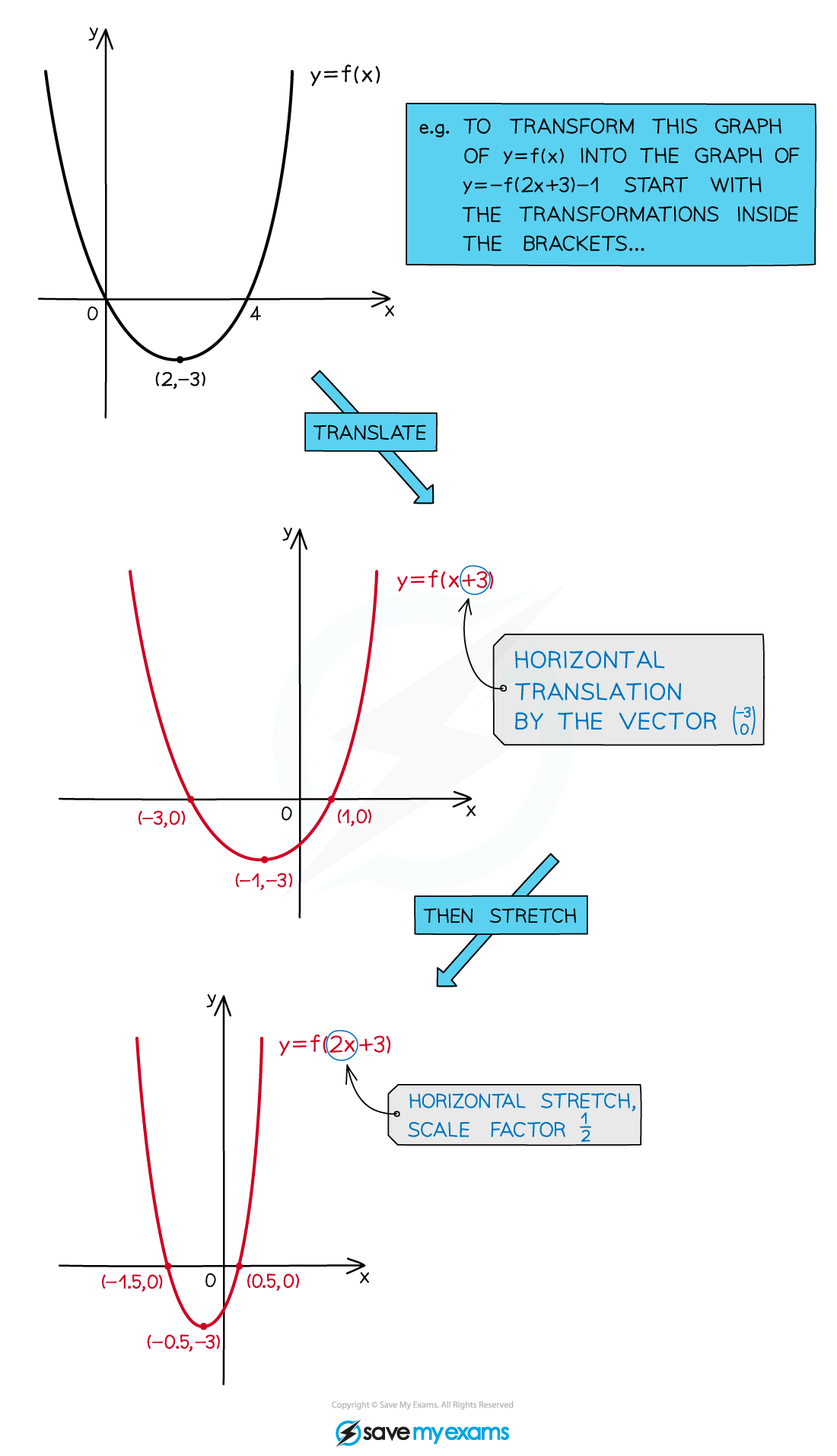
- First apply any horizontal transformations inside the brackets (if you have more than one transformation inside the brackets, translations must be applied before stretches and reflections)
- y = kf(ax + b)+ c
- Then apply any vertical transformations outside the brackets (if you have more than one transformation outside the brackets, stretches and reflections must be applied before translations)
- y = kf(ax + b)+ c
- First apply any horizontal transformations inside the brackets (if you have more than one transformation inside the brackets, translations must be applied before stretches and reflections)
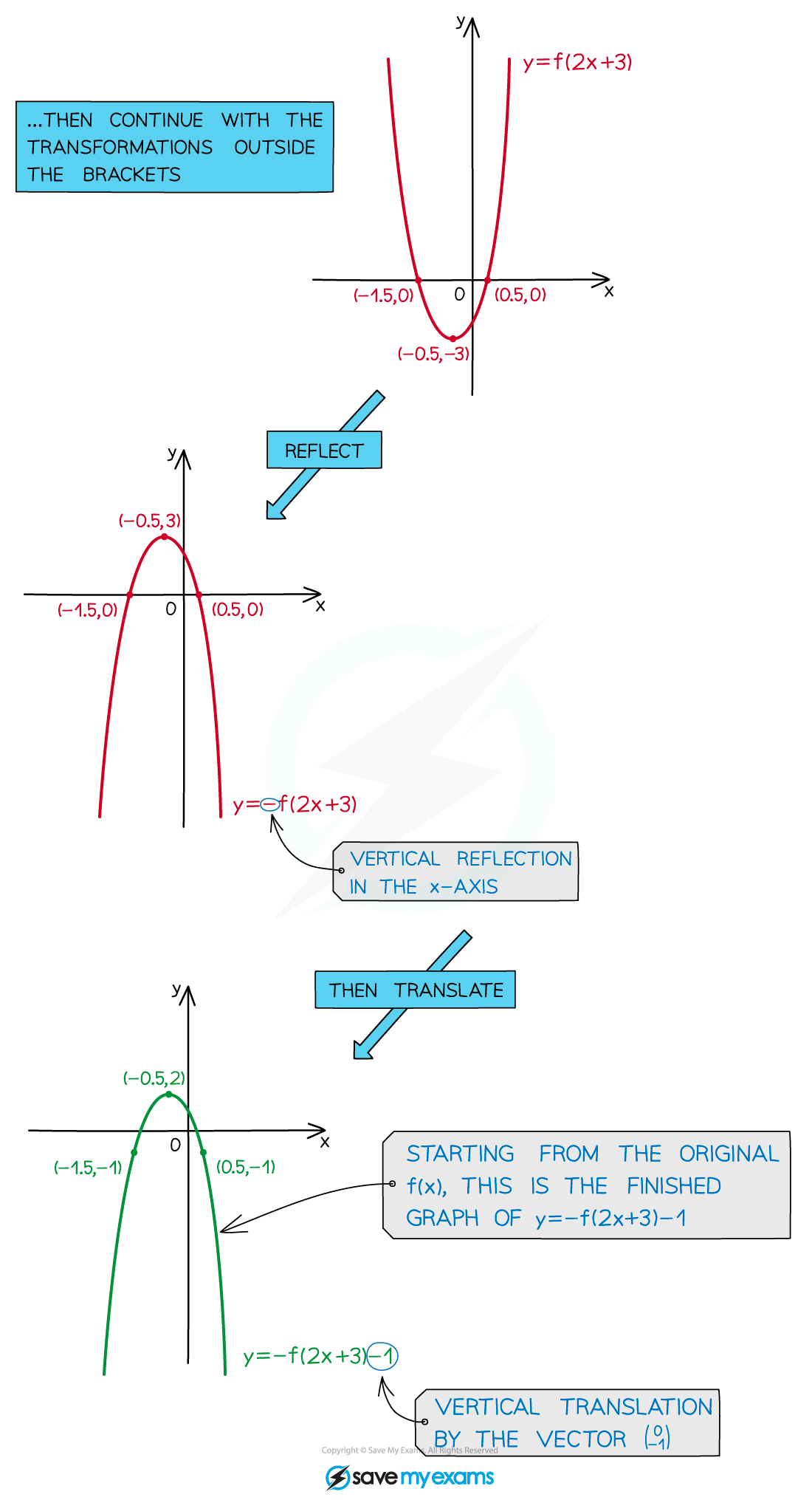
- Any asymptotes of the function are also affected by the combined transformation (perform the transformations one at a time in the same order as above)
Exam Tip
- Be sure to apply transformations in the correct order – applying them in the wrong order can produce an incorrect transformation.
- When you sketch a transformed graph, indicate the new coordinates of any points that are marked on the original graph.
- Try to indicate the coordinates of points where the transformed graph intersects the coordinate axes (although if you don't have the equation of the original function this may not be possible).
- If the graph has asymptotes, don't forget to sketch the asymptotes of the transformed graph as well.
Worked Example

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









