Edexcel A Level Maths: Mechanics:复习笔记4.1.3 Centres of Mass
Uniform Rods & Laminae
What is meant by the centre of mass of an object?
- The centre of mass of an object is the point at which the weight of the object may be considered to act
- For a uniform object the centre of mass is at the centre of the object where the lines of symmetry intersect
- For a uniform rod this will be at its midpoint
- For a uniform rectangular lamina this will be where the diagonals intersect
- For a non-uniform object the centre of mass is not necessarily at the centre of the object
How can I solve problems involving uniform rods?
- If you are told that a rod is uniform then you can draw the weight at the midpoint of the rod
- If a rod lies on a support or peg then there will be a normal reaction force which acts perpendicular to the rod at that point
- If the rod is suspended by strings or cables then there will be tensions in the strings which keep the rod in place
Worked Example
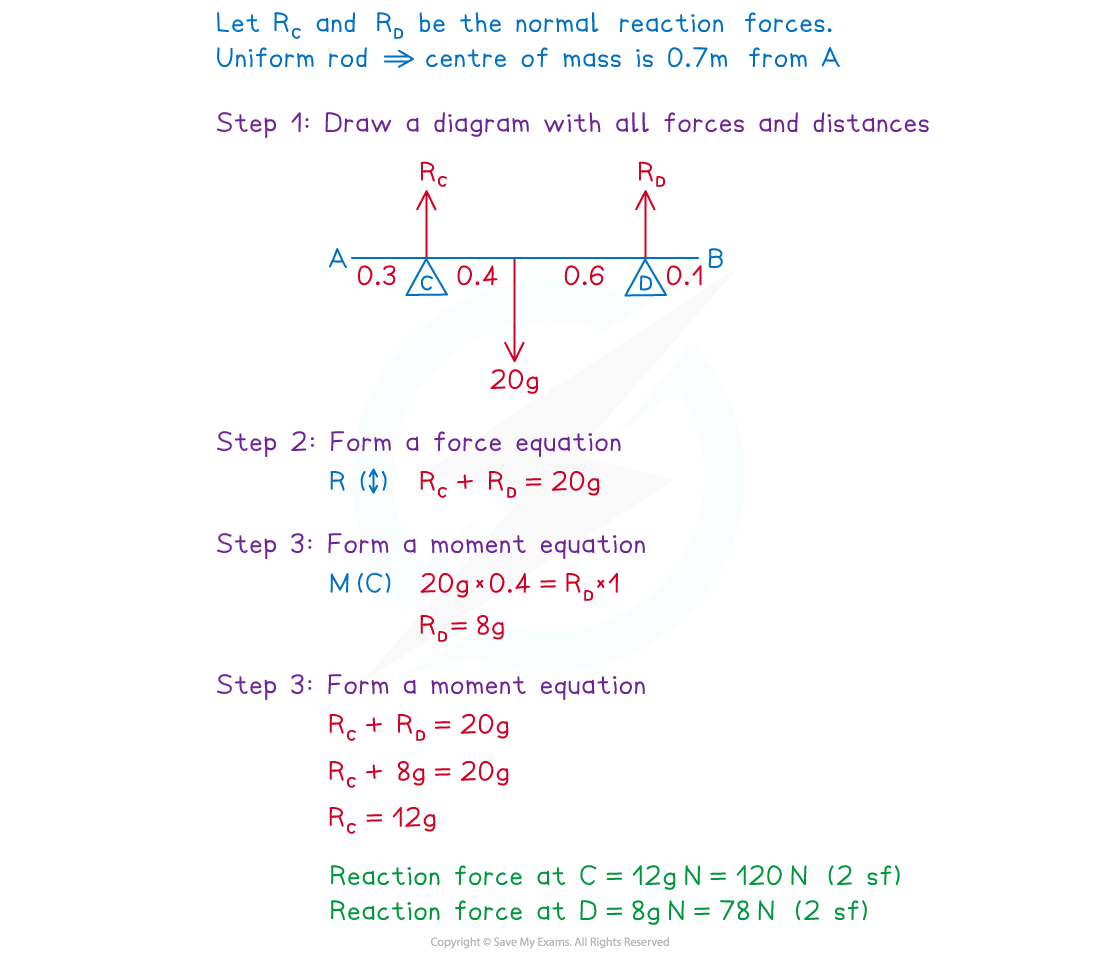
Exam Tip
- If there are two supports with unknown reaction forces then choosing the pivot to be at one of the supports will help to find the force at the other support. The same method works with strings too.
Non-uniform Rods
How do I find the centre of mass of a non-uniform rod in equilibrium?
- Step 1: Label the weight of the rod at a random point on the rod
- Step 2: Call the perpendicular distance between the pivot and the weight x
- Or any letter of your choice
- Step 3: Form a moment equation using the fact that the rod is in equilibrium
- Step 4: Solve the equation to find x
Worked Example
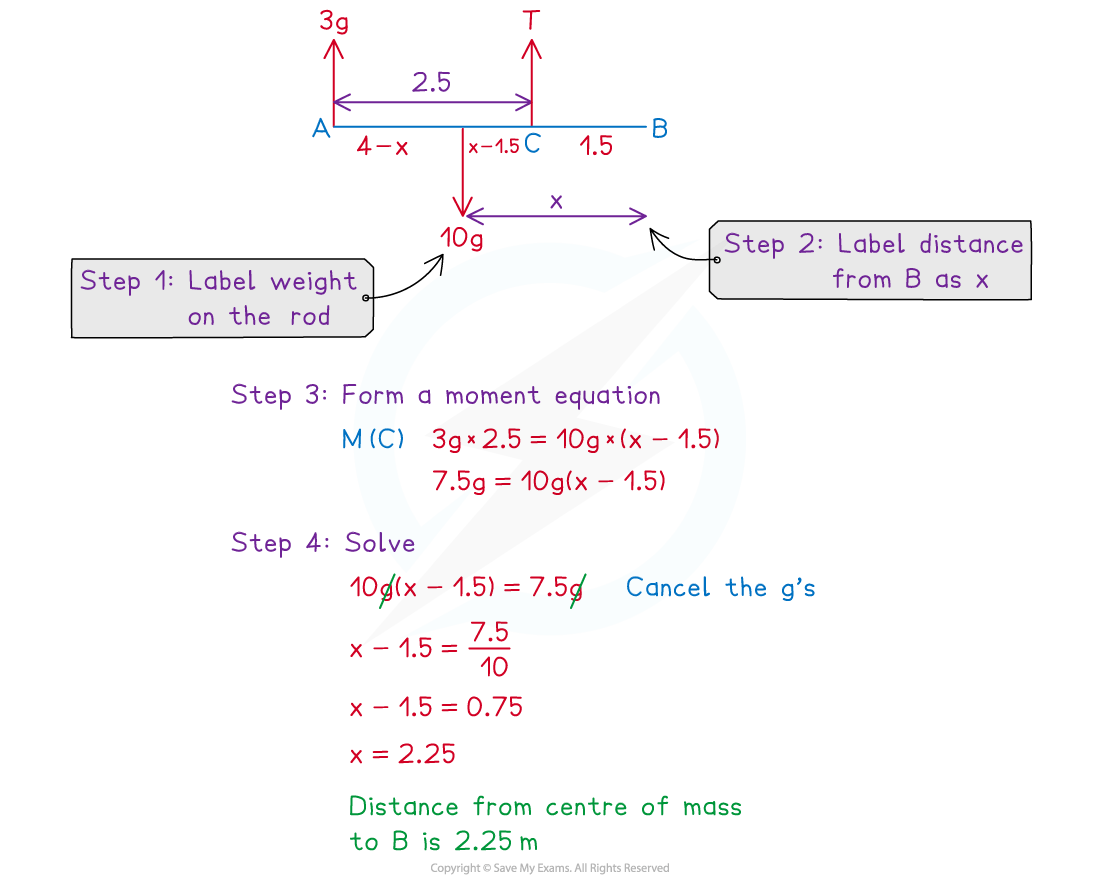
Exam Tip
- Make sure you read carefully which distance you are asked to find.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
