Edexcel A Level Maths: Mechanics:复习笔记2.6.1 Horizontal & Vertical Components

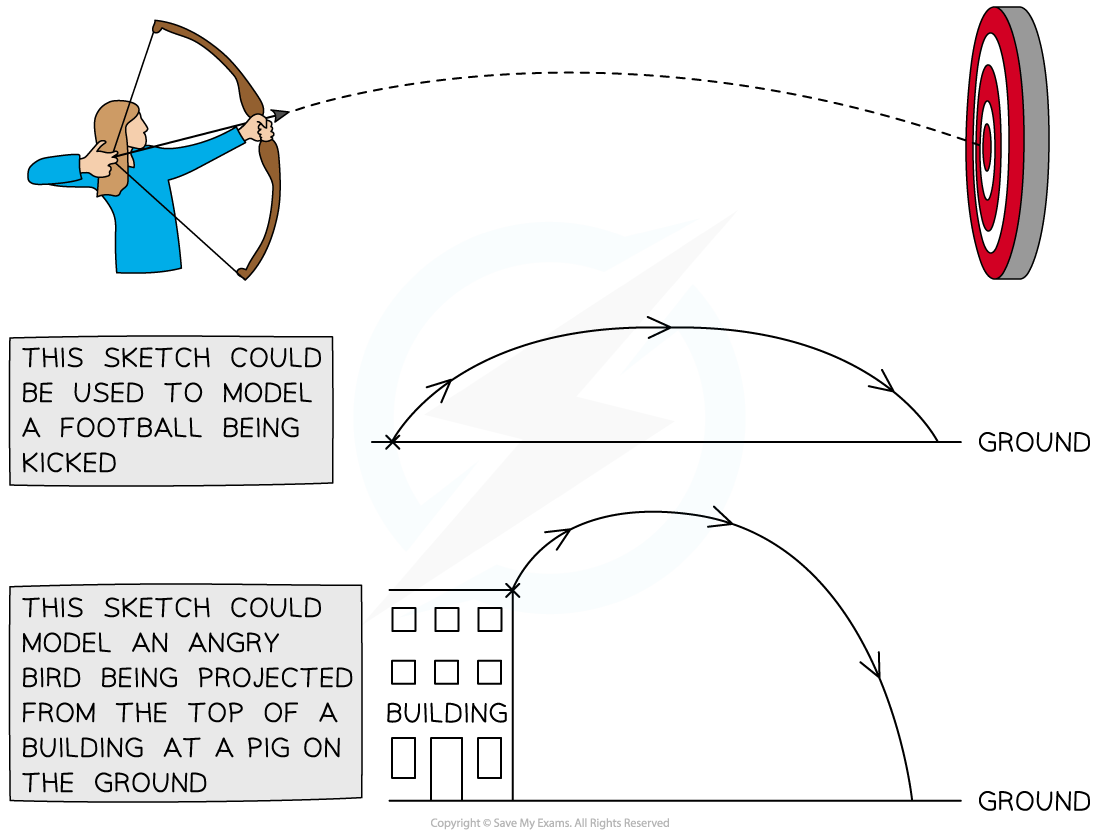
What is a projectile?

• A projectile is a particle moving freely, under gravity, in a two-dimensional plane
• Examples of projectile motion include
  • Sports such as basketball, javelin, archery, etc
  • Computer games such as Angry Birds

  

Modelling assumptions with projectiles?

• The modelling assumptions with projectiles are
  • No air resistance, no horizontal forces
  • The projectile moves freely under gravity (no other vertical forces)
  • Ignore spin and the rotation of the projectile
  • Motion is symmetrical along the path of a parabola

   

What is the acceleration of a projectile?

• As it is 2D there will be a horizontal component to acceleration (ax)and a vertical component (ay)
• There will be no horizontal acceleration (ax = 0)
  • No forces are acting horizontally
  • Horizontal speed is constant

   

• There will be constant vertical acceleration (due to gravity, ay = ± g)
• ay may be positive or negative depending on which direction is taken as positive
• The acceleration can be written as 2D vector

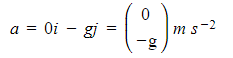
What is the initial velocity of a projectile?

• As it is 2D there will be a horizontal component to the initial velocity(ux) and a vertical component (uy)
• A projectile is launched with initial speed U m s-1 at an angle θ to the horizontal
  • If it is projected below the horizontal then θ would be negative
• Its initial velocity, u m s-1, is a vector with:
  • horizontal component, ux = U cosθ
  • vertical component, uy = U sinθ
• The initial velocity can have a positive or negative vertical component as an object can be projected upwards or downwards

A projectile is launched at an angle of 25° to the horizontal with speed 5 m s-1 .

Find the initial velocity, u m s-1 , of the projectile.