Edexcel A Level Maths: Mechanics:复习笔记2.2.1 Using Calculus in 1D

How is calculus used in kinematics?

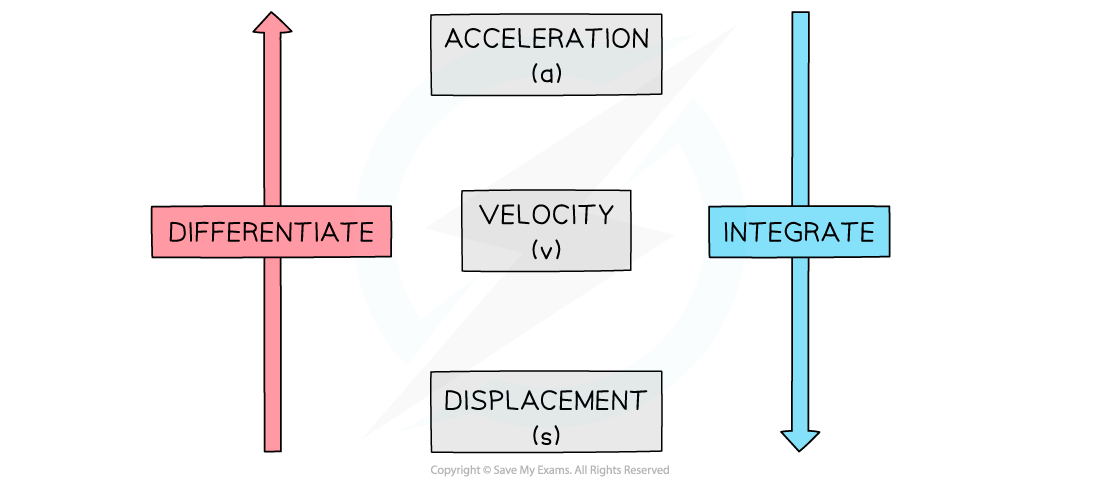
• s, v and a are all functions of time
• Velocity, v, is the rate of change of displacement, s, with respect to time
• Acceleration, a, is the rate of change of velocity, v, with respect to time
• Differentiate to go from s to v and from v to a
• Integrate to go from a to v and from v to s
  • There will be a constant of integration, c, each time you integrate
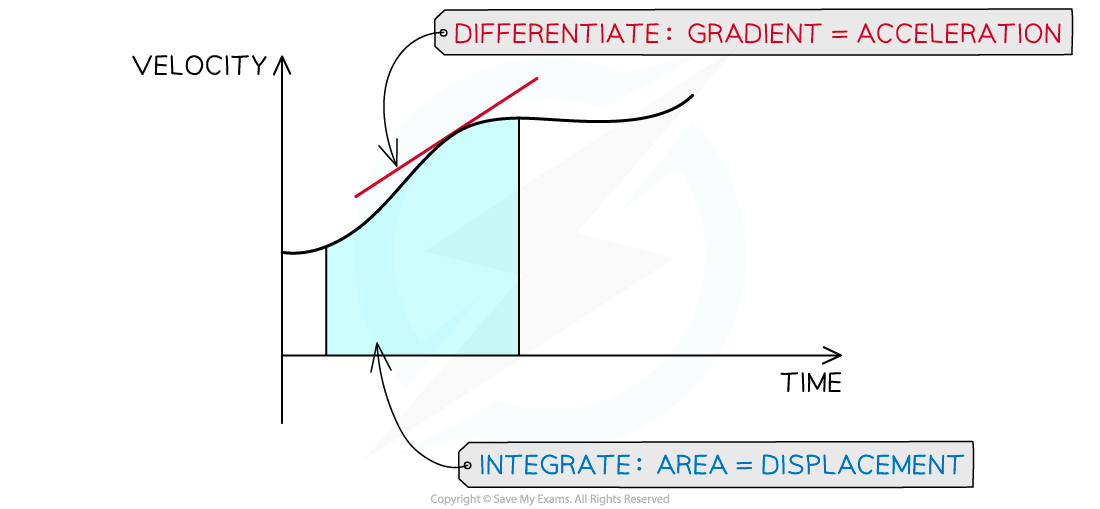
• The use of calculus can be seen using velocity-time graphs
  • Acceleration is the gradient which is found using differentiation
  • Displacement is the area under the graph which is found using integration

  

How do I find c (the constant of integration) in kinematics?

• The value of c can be found by substituting known values, as in integration for pure maths
• Information to find c may be given in words – look out for common phrases …
  • “… starting from rest …”: this means v = 0 when t = 0
  • “… initially …” – this means t = 0

   

Definite integration in kinematics

• Integrating acceleration between two values of time gives the change in velocity of the object between those times
• Integrating velocity between two values of time gives the displacement of the object between those times
  • This could be different to the distance travelled between those times
  • To find the total distance travelled you would need to calculate the areas above and below the x-axis separately

   

(a)  Find the acceleration of the particle in terms of .

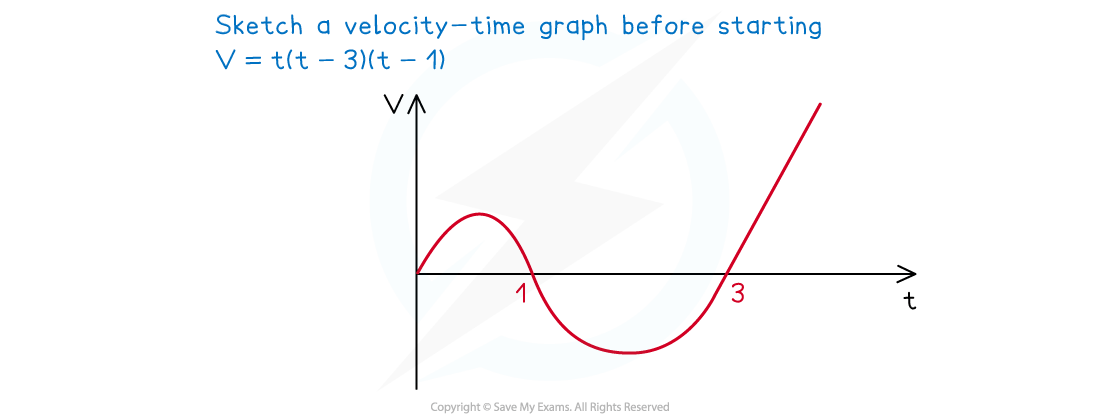
(b)  Find the displacement of the particle, from its starting position, after 3 seconds.