Edexcel A Level Further Maths: Core Pure:复习笔记9.1.1 Intro to Proof by Induction
Intro to Proof by Induction
What is proof by induction?
- Proof by induction is a way of proving a result is true for a set of integers by showing that if it is true for one integer then it is true for the next integer
- It can be thought of as dominoes:
- All dominoes will fall down if:
- The first domino falls down
- Each domino falling down causes the next domino to fall down
- All dominoes will fall down if:
What are the steps for proof by induction?
- STEP 1: The basic step
- Show the result is true for the base case
- This is normally n = 1 or 0 but it could be any integer
- In the dominoes analogy this is showing that the first domino falls down
- STEP 2: The assumption step
- Assume the result is true for n = k for some integer k
- In the dominoes analogy this is assuming that a random domino falls down
- There is nothing to do for this step apart from writing down the assumption
- Assume the result is true for n = k for some integer k
- STEP 3: The inductive step
- Using the assumption show the result is true for n = k + 1
- The assumption from STEP 2 will be needed at some point
- In the dominoes analogy this is showing that the random domino that we assumed falls down will cause the next one to fall down
- STEP 4: The conclusion step
- State the result is true
- Explain in words why the result is true
- It must include:
- If true for n = k then it is true for n = k + 1
- Since true for n = 1 the statement is true for all n ∈ ℤ, n ≥ 1 by mathematical induction
- The sentence will be the same for each proof just change the base case from n = 1 if necessary
What type of statements might I be asked to prove by induction?
- There are 4 main applications that you could be asked
- Formulae for sums of series
- Formulae for recursive sequences
- Expression for the power of a matrix
- Showing an expression is always divisible by a specific value
- Induction is always used to prove de Moivre's theorem
- It is unlikely that you will be asked unfamiliar applications in your exam but induction is used in other areas of maths
- Proving formulae for nth derivative of functions
- Proving formulae involving factorials
Proving de Moivre's Theorem by Induction
How is de Moivre’s Theorem proved?
- When written in Euler’s form the proof of de Moivre’s theorem is easy to see:
- Using the index law of brackets:
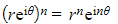
- Using the index law of brackets:
- However Euler’s form cannot be used to prove de Moivre’s Theorem when it is in modulus-argument (polar) form
- Proof by induction can be used to prove de Moivre’s Theorem for positive integers:
- To prove de Moivre’s Theorem for all positive integers, n
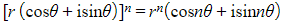
- STEP 1: Prove it is true for n = 1
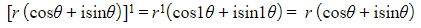
- So de Moivre’s Theorem is true for n = 1
- STEP 2: Assume it is true for n = k
- STEP 3: Show it is true for n = k + 1
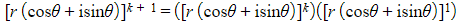
- According to the assumption this is equal to
- Using laws of indices and multiplying out the brackets:
- =
- =
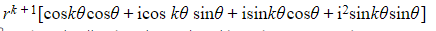
- Letting i2 = -1 and collecting the real and imaginary parts gives:
- =
- =
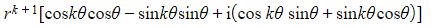
- Recognising that the real part is equivalent to cos(kθ + θ ) and the imaginary part is equivalent to sin(kθ + θ ) gives
- =
- =
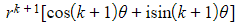
- So de Moivre’s Theorem is true for n = k + 1
- STEP 4: Write a conclusion to complete the proof
- The statement is true for n = 1, and if it is true for n = k it is also true for n = k + 1
- Therefore, by the principle of mathematical induction, the result is true for all positive integers, n
- De Moivre’s Theorem works for all real values of n
- However you could only be asked to prove it is true for positive integers
Worked Example
Show, using proof by mathematical induction, that for a complex number 
and for all positive integers, n,
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
