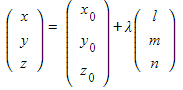- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记6.2.2 Combinations of Lines & Planes
Intersections of Lines & Planes
How do I tell if a line is parallel to a plane?
- A line is parallel to a plane if its direction vector is perpendicular to the plane’s normal vector
- If you know the Cartesian equation of the plane in the form
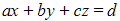 then the values of a, b, and c are the individual components of a normal vector to the plane
then the values of a, b, and c are the individual components of a normal vector to the plane - The scalar product can be used to check in the direction vector and the normal vector are perpendicular
- If two vectors are perpendicular their scalar product will be zero
How do I tell if the line lies inside the plane?
- If the line is parallel to the plane then it will either never intersect or it will lie inside the plane
- Check to see if they have a common point
- If a line is parallel to a plane and they share any point, then the line lies inside the plane
How do I find the point of intersection of a line and a plane in Cartesian form?
- If a line is not parallel to a plane it will intersect it at a single point
- If both the vector equation of the line and the Cartesian equation of the plane is known then this can be found by:
- STEP 1: Set the position vector of the point you are looking for to have the individual components x, y, and z and substitute into the vector equation of the line
- STEP 2: Find the parametric equations in terms of x, y, and z
- STEP 3: Substitute these parametric equations into the Cartesian equation of the plane and solve to find λ
- STEP 4: Substitute this value of λ back into the vector equation of the line and use it to find the position vector of the point of intersection
- STEP 5: Check this value in the Cartesian equation of the plane to make sure you have the correct answer
How do I find the point of intersection of a line and a plane in vector form?
- Suppose you have a line with equation
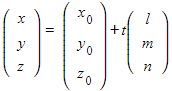 and plane with equation
and plane with equation 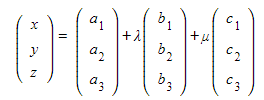
- Form three equations with unknowns t, λ and μ
- Solve them simultaneously on your calculator
- Substitute the values back in to get the intersection
Worked Example
Find the point of intersection of the line 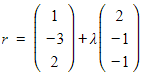 with the plane
with the plane ![]()

Angle between a Line & a Plane
How do I find the angle between a line and a plane?
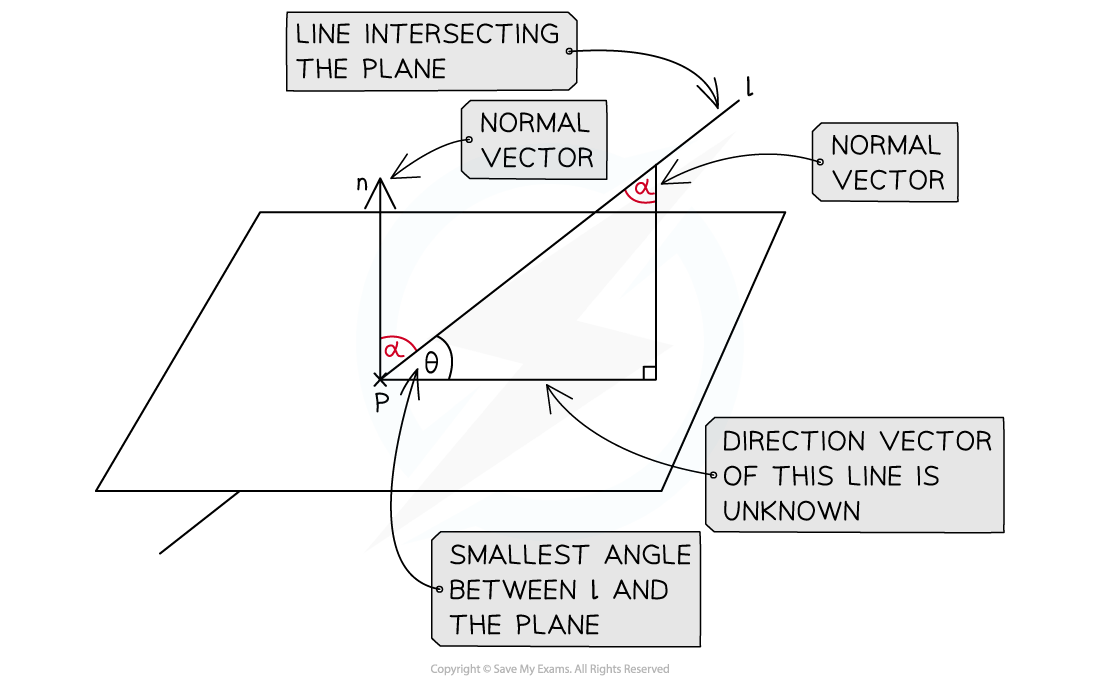
- When you find the angle between a line and a plane you will be finding the angle between the line itself and the line on the plane that creates the smallest angle with it
- This means the line on the plane directly under the line as it joins the plane
- It is easiest to think of these two lines making a right-triangle with the normal vector to the plane
- The line joining the plane will be the hypotenuse
- The line on the plane will be adjacent to the angle
- The normal will the opposite the angle
- As you do not know the angle of the line on the plane you can instead find the angle between the normal and the hypotenuse
- This is the angle opposite the angle you want to find
- This angle can be found because you will know the direction vector of the line joining the plane and the normal vector to the plane
- This angle is also equal to the angle made by the line at the point it joins the plane and the normal vector at this point
- The smallest angle between the line and the plane will be 90° minus the angle between the normal vector and the line
- In radians this will be
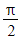 minus the angle between the normal vector and the line
minus the angle between the normal vector and the line
- In radians this will be
Exam Tip
- Remember that if the scalar product is negative your answer will result in an obtuse angle
- Taking the absolute value of the scalar product will ensure that you get the acute angle as your answer
Worked Example
Find the angle in radians between the line L with vector equation ![]() and the plane
and the plane ![]() with Cartesian equation
with Cartesian equation ![]() .
.

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1