Edexcel A Level Further Maths: Core Pure:复习笔记6.1.2 Pairs of Lines in 3D
Coincident & Parallel Lines
How do I tell if two lines are parallel?
- Two lines are parallel if, and only if, their direction vectors are parallel
- This means the direction vectors will be scalar multiples of each other
- For example, the lines whose equations are
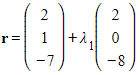and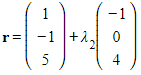 
are parallel
- This is because
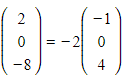
- This is because
How do I tell if two lines are coincident?
- Coincident lines are two lines that lie directly on top of each other
- They are indistinguishable from each other
- Two parallel lines will either never intersect or they are coincident (identical)
- Sometimes the vector equations of the lines may look different
- for example, the lines represented by the equations
and 
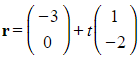are coincident,
- for example, the lines represented by the equations
- To check whether two lines are coincident:
- First check that they are parallel
- They are because
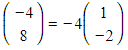and so their direction vectors are parallel
- They are because
- Next, determine whether any point on one of the lines also lies on the other
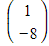is the position vector of a point on the first line and 
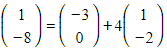so it also lies on the second line
- If two parallel lines share any point, then they share all points and are coincident
- First check that they are parallel
- Sometimes the vector equations of the lines may look different
Intersecting Lines
How do I determine whether two lines in 3 dimensions intersect?
- If the lines are not parallel, check whether they intersect:
- STEP 1: Set the vector equations of the two lines equal to each other with different variables
- e.g. λ and μ, for the parameters
- STEP 2: Write the three separate equations for the i, j, and k components in terms of λ and μ
- STEP 3: Solve two of the equations to find a value for λ and μ
- STEP 4: Check whether the values of λ and μ you have found satisfy the third equation
- If all three equations are satisfied, then the lines intersect
- STEP 1: Set the vector equations of the two lines equal to each other with different variables
How do I find the point of intersection of two lines?
- If a pair of lines are not parallel and do intersect, a unique point of intersection can be found
- If the two lines intersect, there will be a single point that will lie on both lines
- Follow the steps above to find the values of λ and μ that satisfy all three equations
- STEP 5: Substitute either the value of λ or the value of μ into one of the vector equations to find the position vector of the point where the lines intersect
- It is always a good idea to check in the other equations as well, you should get the same point for each line
Exam Tip
- Make sure that you use different letters, e.g. λ and μ, to represent the parameters in vector equations of different lines
- Check that the variable you are using has not already been used in the question
Worked Example
Line L1 has vector equation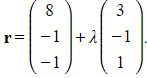 
.
Line L2 has vector equation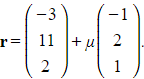 
.
a) Show that the lines L1 and L2 intersect.
b) Find the position vector of the point of intersection.
Skew Lines
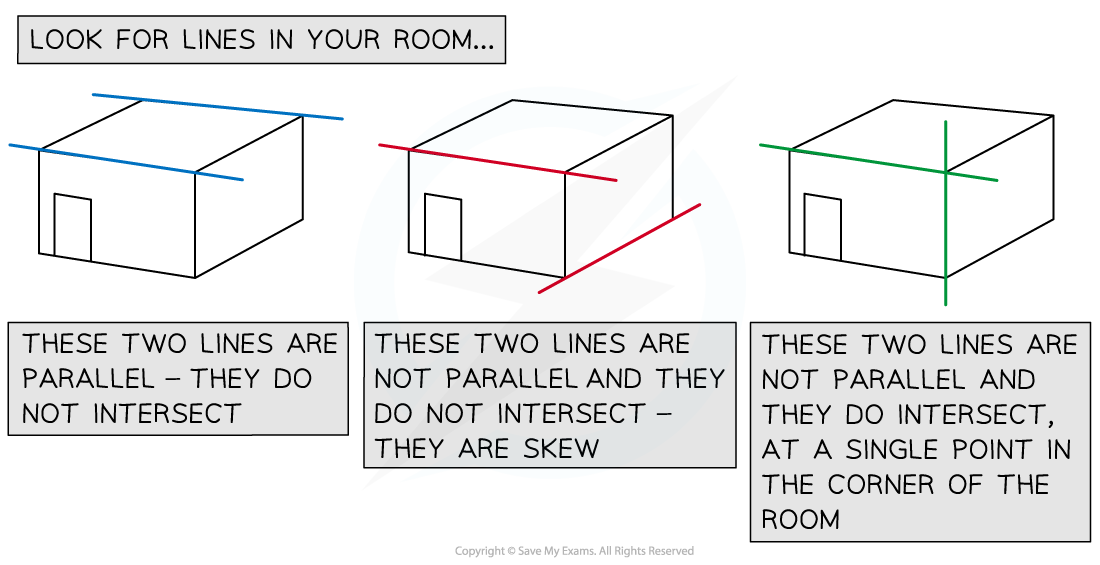
What are skew lines?
- Lines that are not parallel and which do not intersect are called skew lines
- This is only possible in 3-dimensions
- If two lines are skew then there is not a plane in 3D than contains both of the lines
How do I determine whether lines in 3 dimensions are parallel, skew, or intersecting?
- First, look to see if the direction vectors are parallel:
- if the direction vectors are parallel, then the lines are parallel
- if the direction vectors are not parallel, the lines are not parallel
- If the lines are parallel, check to see if the lines are coincident:
- If they share any point, then they are coincident
- If any point on one line is not on the other line, then the lines are not coincident
- If the lines are not parallel, check whether they intersect:
- STEP 1: Set the vector equations of the two lines equal to each other with different variables
- e.g. λ and μ, for the parameters
- STEP 2: Write the three separate equations for the i, j, and k components in terms of λ and μ
- STEP 3: Solve two of the equations to find a value for λ and μ
- STEP 4: Check whether the values of λ and μ you have found satisfy the third equation
- If all three equations are satisfied, then the lines intersect
- If not all three equations are satisfied, then the lines are skew
- STEP 1: Set the vector equations of the two lines equal to each other with different variables
Worked Example
Determine whether the following pair of lines are parallel, intersect, or are skew.
.
转载自savemyexams
翰林AMC8视频课重磅上线！
国际竞赛真题资源免费领取
