- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记5.2.2 Mean Value of a Function
Mean Value of a Function
What is the mean value of a function?
- The mean value of a function may be thought of as the ‘average’ value of a function over a given interval
- For a function f(x), the mean value of the function over the interval [a, b] is given by
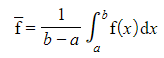
-
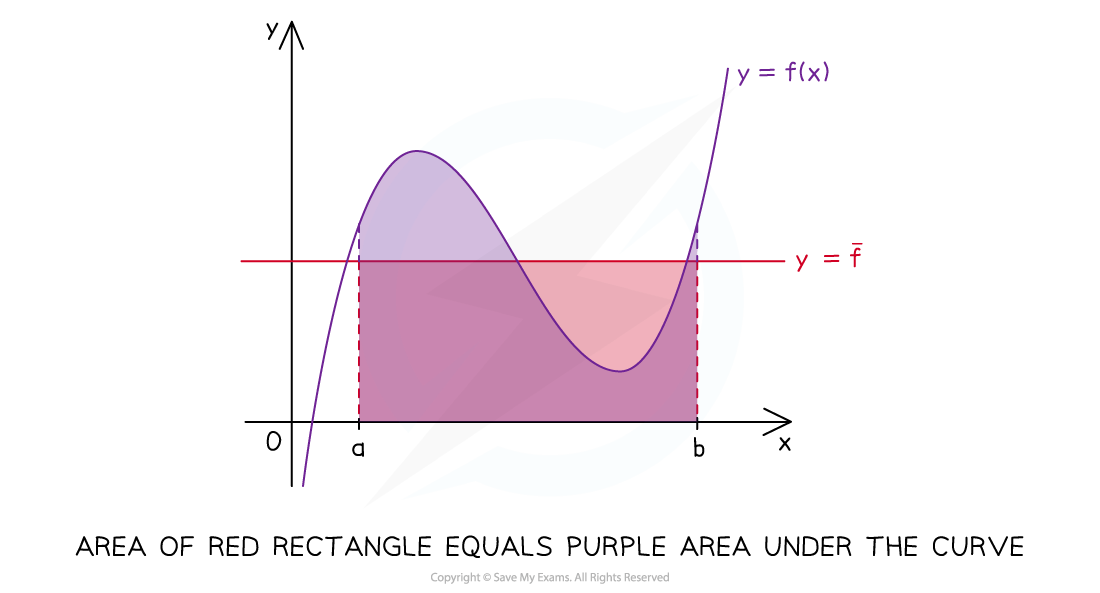
- Note that the mean value
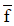 is simply a real number – it is not a function
is simply a real number – it is not a function - The mean value depends on the interval chosen – if the interval [a, b] changes, then the mean value may change as well
- Note that the mean value
- Because
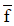 is a real number, the graph of
is a real number, the graph of 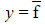 is a horizontal line
is a horizontal line
- This gives a geometrical interpretation of the mean value of a function over a given interval
- If A is the area bounded by the curve y = f(x), the x-axis and the lines x = a and x = b, then the rectangle with its base on the interval [a, b] and with height also has area A
- i.e.
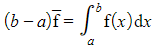
- i.e.
What are the properties of the mean value of a function?
- If
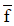 is the mean value of a function f(x) over the interval [a, b], and k is a real constant, then:
is the mean value of a function f(x) over the interval [a, b], and k is a real constant, then:
- f(x) + k has mean value
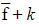 over the interval [a, b]
over the interval [a, b] - kf(x) has mean value
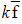 over the interval [a, b]
over the interval [a, b] - -f(x) has mean value -
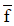 over the interval [a, b]
over the interval [a, b]
- f(x) + k has mean value
- If
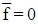 then the area that is above the x-axis and under the curve is equal to the area that is below the x-axis and above the curve
then the area that is above the x-axis and under the curve is equal to the area that is below the x-axis and above the curve
Worked Example
Let ![]() be the function defined by
be the function defined by ![]() .
.
a) Find the exact mean value of 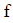 over the interval
over the interval 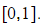 .
.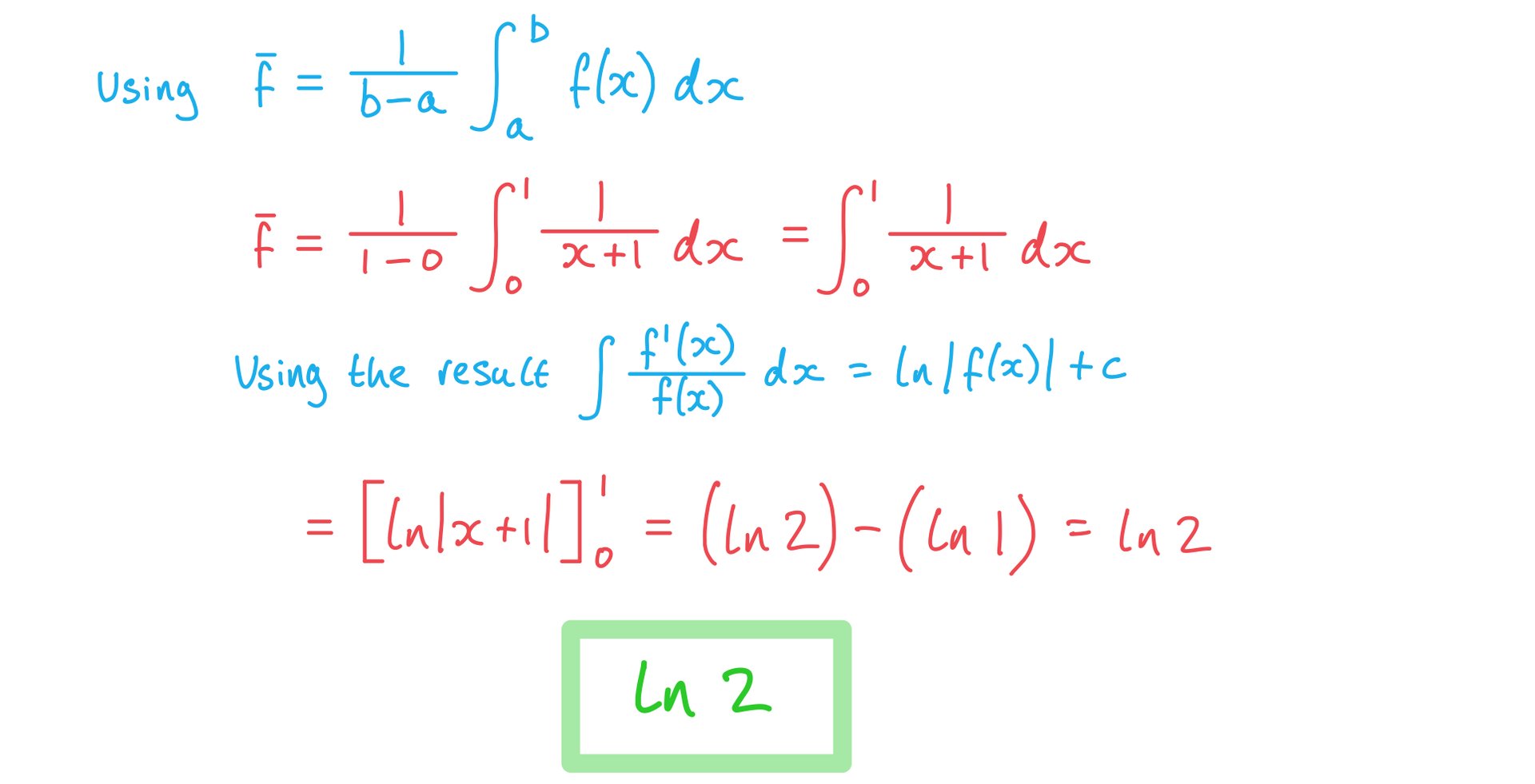
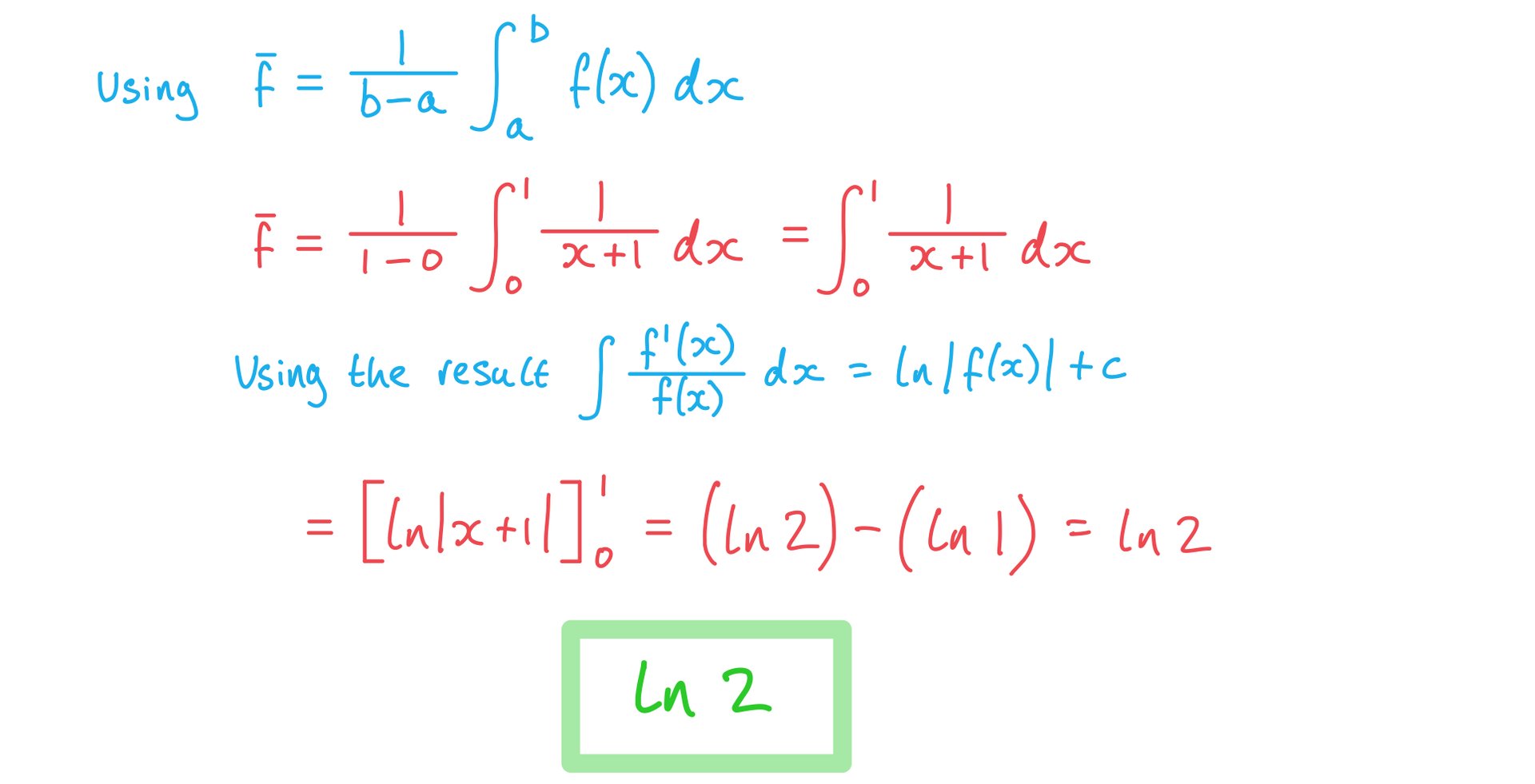
b) Write down the exact mean value of each of the following functions over the interval 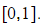 :
:
(i)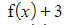
(ii)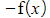
(iii)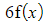

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








