- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2015 AIME II真题及答案解析
2015 AIME II真题
答案解析请参考文末
Problem 1
Let ![]() be the least positive integer that is both
be the least positive integer that is both ![]() percent less than one integer and
percent less than one integer and ![]() percent greater than another integer. Find the remainder when
percent greater than another integer. Find the remainder when ![]() is divided by
is divided by ![]() .
.
Problem 2
In a new school, ![]() percent of the students are freshmen,
percent of the students are freshmen, ![]() percent are sophomores,
percent are sophomores, ![]() percent are juniors, and
percent are juniors, and ![]() percent are seniors. All freshmen are required to take Latin, and
percent are seniors. All freshmen are required to take Latin, and ![]() percent of sophomores,
percent of sophomores, ![]() percent of the juniors, and
percent of the juniors, and ![]() percent of the seniors elect to take Latin. The probability that a randomly chosen Latin student is a sophomore is
percent of the seniors elect to take Latin. The probability that a randomly chosen Latin student is a sophomore is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 3
Let ![]() be the least positive integer divisible by
be the least positive integer divisible by ![]() whose digits sum to
whose digits sum to ![]() . Find
. Find ![]() .
.
Problem 4
In an isosceles trapezoid, the parallel bases have lengths ![]() and
and ![]() , and the altitude to these bases has length
, and the altitude to these bases has length ![]() . The perimeter of the trapezoid can be written in the form
. The perimeter of the trapezoid can be written in the form ![]() , where
, where ![]() and
and ![]() are positive integers. Find
are positive integers. Find ![]() .
.
Problem 5
Two unit squares are selected at random without replacement from an ![]() grid of unit squares. Find the least positive integer
grid of unit squares. Find the least positive integer ![]() such that the probability that the two selected unit squares are horizontally or vertically adjacent is less than
such that the probability that the two selected unit squares are horizontally or vertically adjacent is less than ![]() .
.
Problem 6
Steve says to Jon, "I am thinking of a polynomial whose roots are all positive integers. The polynomial has the form ![]() for some positive integers
for some positive integers ![]() and
and ![]() . Can you tell me the values of
. Can you tell me the values of ![]() and
and ![]() ?"
?"
After some calculations, Jon says, "There is more than one such polynomial."
Steve says, "You're right. Here is the value of ![]() ." He writes down a positive integer and asks, "Can you tell me the value of
." He writes down a positive integer and asks, "Can you tell me the value of ![]() ?"
?"
Jon says, "There are still two possible values of ![]() ."
."
Find the sum of the two possible values of ![]() .
.
Problem 7
Triangle ![]() has side lengths
has side lengths ![]() ,
, ![]() , and
, and ![]() . Rectangle
. Rectangle ![]() has vertex
has vertex ![]() on
on ![]() , vertex
, vertex ![]() on
on ![]() , and vertices
, and vertices ![]() and
and ![]() on
on ![]() . In terms of the side length
. In terms of the side length ![]() , the area of
, the area of ![]() can be expressed as the quadratic polynomial
can be expressed as the quadratic polynomial
![]() .
.
Then the coefficient ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 8
Let ![]() and
and ![]() be positive integers satisfying
be positive integers satisfying ![]() . The maximum possible value of
. The maximum possible value of ![]() is
is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 9
A cylindrical barrel with radius ![]() feet and height
feet and height ![]() feet is full of water. A solid cube with side length
feet is full of water. A solid cube with side length ![]() feet is set into the barrel so that the diagonal of the cube is vertical. The volume of water thus displaced is
feet is set into the barrel so that the diagonal of the cube is vertical. The volume of water thus displaced is ![]() cubic feet. Find
cubic feet. Find ![]() .
.
![[asy] import three; import solids; size(5cm); currentprojection=orthographic(1,-1/6,1/6); draw(surface(revolution((0,0,0),(-2,-2*sqrt(3),0)--(-2,-2*sqrt(3),-10),Z,0,360)),white,nolight); triple A =(8*sqrt(6)/3,0,8*sqrt(3)/3), B = (-4*sqrt(6)/3,4*sqrt(2),8*sqrt(3)/3), C = (-4*sqrt(6)/3,-4*sqrt(2),8*sqrt(3)/3), X = (0,0,-2*sqrt(2)); draw(X--X+A--X+A+B--X+A+B+C); draw(X--X+B--X+A+B); draw(X--X+C--X+A+C--X+A+B+C); draw(X+A--X+A+C); draw(X+C--X+C+B--X+A+B+C,linetype("2 4")); draw(X+B--X+C+B,linetype("2 4")); draw(surface(revolution((0,0,0),(-2,-2*sqrt(3),0)--(-2,-2*sqrt(3),-10),Z,0,240)),white,nolight); draw((-2,-2*sqrt(3),0)..(4,0,0)..(-2,2*sqrt(3),0)); draw((-4*cos(atan(5)),-4*sin(atan(5)),0)--(-4*cos(atan(5)),-4*sin(atan(5)),-10)..(4,0,-10)..(4*cos(atan(5)),4*sin(atan(5)),-10)--(4*cos(atan(5)),4*sin(atan(5)),0)); draw((-2,-2*sqrt(3),0)..(-4,0,0)..(-2,2*sqrt(3),0),linetype("2 4")); [/asy]](http://latex.artofproblemsolving.com/9/e/a/9ea530dcf8660904fcdb6c7e02d431954bb03eda.png)
Problem 10
Call a permutation ![]() of the integers
of the integers ![]() quasi-increasing if
quasi-increasing if ![]() for each
for each ![]() . For example,
. For example, ![]() and
and ![]() are quasi-increasing permutations of the integers
are quasi-increasing permutations of the integers ![]() , but
, but ![]() is not. Find the number of quasi-increasing permutations of the integers
is not. Find the number of quasi-increasing permutations of the integers ![]() .
.
Problem 11
The circumcircle of acute ![]() has center
has center ![]() . The line passing through point
. The line passing through point ![]() perpendicular to
perpendicular to ![]() intersects lines
intersects lines ![]() and
and ![]() at
at ![]() and
and ![]() , respectively. Also
, respectively. Also ![]() ,
, ![]() ,
, ![]() , and
, and ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 12
There are ![]() possible
possible ![]() -letter strings in which each letter is either an A or a B. Find the number of such strings that do not have more than
-letter strings in which each letter is either an A or a B. Find the number of such strings that do not have more than ![]() adjacent letters that are identical.
adjacent letters that are identical.
Problem 13
Define the sequence ![]() by
by ![]() , where
, where ![]() represents radian measure. Find the index of the 100th term for which
represents radian measure. Find the index of the 100th term for which ![]() .
.
Problem 14
Let ![]() and
and ![]() be real numbers satisfying
be real numbers satisfying ![]() and
and ![]() . Evaluate
. Evaluate ![]() .
.
Problem 15
Circles ![]() and
and ![]() have radii
have radii ![]() and
and ![]() , respectively, and are externally tangent at point
, respectively, and are externally tangent at point ![]() . Point
. Point![]() is on
is on ![]() and point
and point ![]() is on
is on ![]() such that
such that ![]() is a common external tangent of the two circles. A line
is a common external tangent of the two circles. A line ![]() through
through ![]() intersects
intersects ![]() again at
again at ![]() and intersects
and intersects ![]() again at
again at ![]() . Points
. Points ![]() and
and ![]() lie on the same side of
lie on the same side of ![]() , and the areas of
, and the areas of ![]() and
and ![]() are equal. This common area is
are equal. This common area is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
![[asy] import cse5; pathpen=black; pointpen=black; size(6cm); pair E = IP(L((-.2476,1.9689),(0.8,1.6),-3,5.5),CR((4,4),4)), D = (-.2476,1.9689); filldraw(D--(0.8,1.6)--(0,0)--cycle,gray(0.7)); filldraw(E--(0.8,1.6)--(4,0)--cycle,gray(0.7)); D(CR((0,1),1)); D(CR((4,4),4,150,390)); D(L(MP("D",D(D),N),MP("A",D((0.8,1.6)),NE),1,5.5)); D((-1.2,0)--MP("B",D((0,0)),S)--MP("C",D((4,0)),S)--(8,0)); D(MP("E",E,N)); [/asy]](http://latex.artofproblemsolving.com/6/b/7/6b7782afc839b219809c6266cec4abca23e9d026.png)
2015 AIME II答案及解析请注册或登录后查看:
以上解析方式仅供参考
翰林AIME课程体系流程图
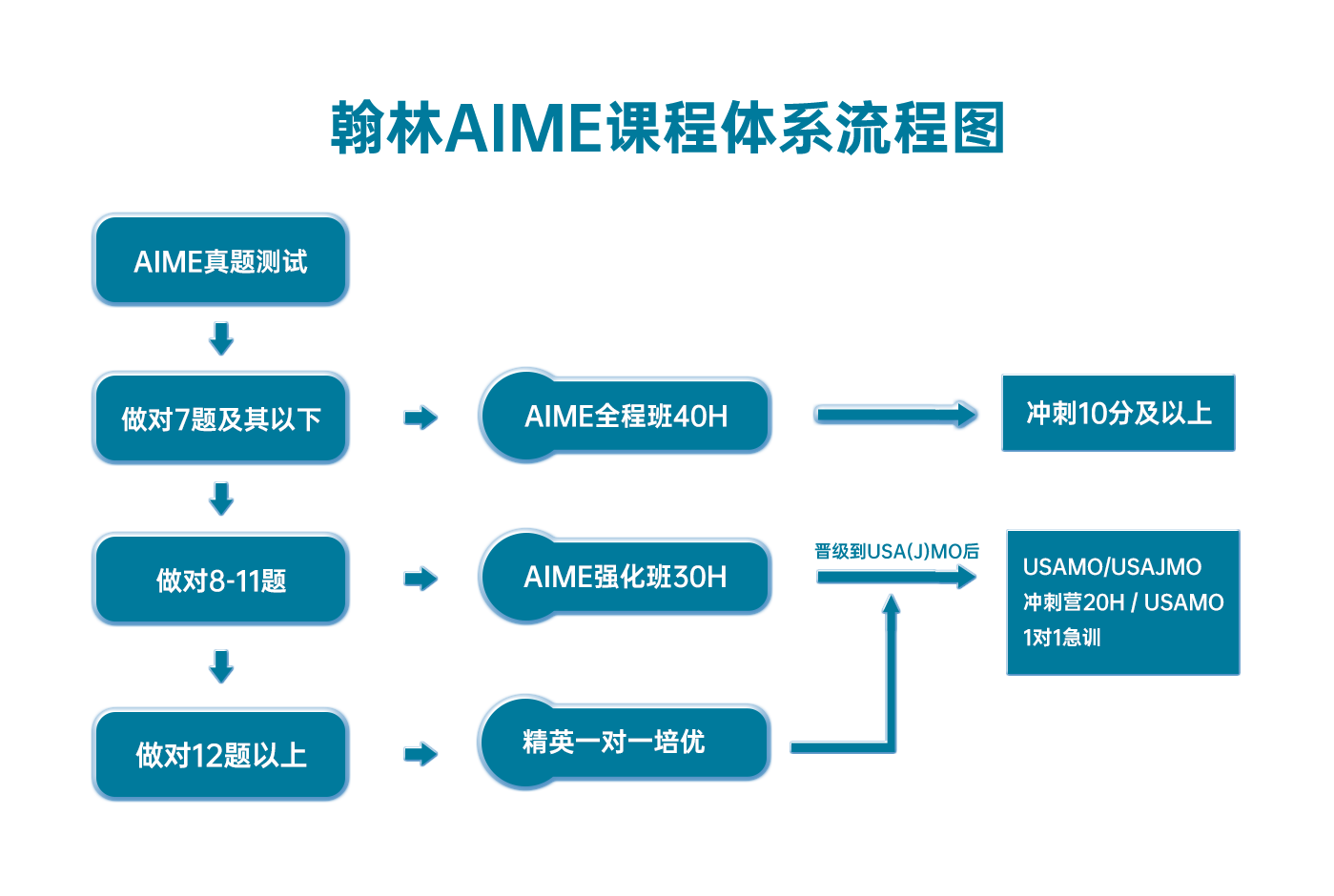
[products columns="2" orderby="title" order="" ids="26004, 720, 719, 718"]

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








