- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
2016 AIME II真题及答案解析
2016 AIME II真题
答案解析请参考文末
[vc_btn title="精编AMC8/10/12/AIME习题集" style="flat" color="primary" size="lg" align="center" i_icon_fontawesome="fa fa-book" css_animation="bounceIn" add_icon="true" link="url:%2Fproduct%2Famc||target:%20_blank"]
Problem 1
Initially Alex, Betty, and Charlie had a total of ![]() peanuts. Charlie had the most peanuts, and Alex had the least. The three numbers of peanuts that each person had formed a geometric progression. Alex eats
peanuts. Charlie had the most peanuts, and Alex had the least. The three numbers of peanuts that each person had formed a geometric progression. Alex eats ![]() of his peanuts, Betty eats
of his peanuts, Betty eats ![]() of her peanuts, and Charlie eats
of her peanuts, and Charlie eats ![]() of his peanuts. Now the three numbers of peanuts each person has forms an arithmetic progression. Find the number of peanuts Alex had initially.
of his peanuts. Now the three numbers of peanuts each person has forms an arithmetic progression. Find the number of peanuts Alex had initially.
Problem 2
There is a ![]() chance of rain on Saturday and a
chance of rain on Saturday and a ![]() chance of rain on Sunday. However, it is twice as likely to rain on Sunday if it rains on Saturday than if it does not rain on Saturday. The probability that it rains at least one day this weekend is
chance of rain on Sunday. However, it is twice as likely to rain on Sunday if it rains on Saturday than if it does not rain on Saturday. The probability that it rains at least one day this weekend is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 3
Let ![]() and
and ![]() be real numbers satisfying the system
be real numbers satisfying the system![]()
![]()
![]() Find the value of
Find the value of ![]() .
.
Problem 4
An ![]() rectangular box is built from
rectangular box is built from ![]() unit cubes. Each unit cube is colored red, green, or yellow. Each of the
unit cubes. Each unit cube is colored red, green, or yellow. Each of the ![]() layers of size
layers of size ![]() parallel to the
parallel to the ![]() faces of the box contains exactly
faces of the box contains exactly ![]() red cubes, exactly
red cubes, exactly ![]() green cubes, and some yellow cubes. Each of the
green cubes, and some yellow cubes. Each of the ![]() layers of size
layers of size ![]() parallel to the
parallel to the ![]() faces of the box contains exactly
faces of the box contains exactly ![]() green cubes, exactly
green cubes, exactly ![]() yellow cubes, and some red cubes. Find the smallest possible volume of the box.
yellow cubes, and some red cubes. Find the smallest possible volume of the box.
Problem 5
Triangle ![]() has a right angle at
has a right angle at ![]() . Its side lengths are pairwise relatively prime positive integers, and its perimeter is
. Its side lengths are pairwise relatively prime positive integers, and its perimeter is ![]() . Let
. Let ![]() be the foot of the altitude to
be the foot of the altitude to ![]() , and for
, and for ![]() , let
, let ![]() be the foot of the altitude to
be the foot of the altitude to ![]() in
in ![]() . The sum
. The sum ![]() . Find
. Find ![]() .
.
Problem 6
For polynomial ![]() , define
, define  . Then
. Then  , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 7
Squares ![]() and
and ![]() have a common center and
have a common center and ![]() . The area of
. The area of ![]() is 2016, and the area of
is 2016, and the area of ![]() is a smaller positive integer. Square
is a smaller positive integer. Square ![]() is constructed so that each of its vertices lies on a side of
is constructed so that each of its vertices lies on a side of ![]() and each vertex of
and each vertex of ![]() lies on a side of
lies on a side of ![]() . Find the difference between the largest and smallest positive integer values for the area of
. Find the difference between the largest and smallest positive integer values for the area of ![]() .
.
Problem 8
Find the number of sets ![]() of three distinct positive integers with the property that the product of
of three distinct positive integers with the property that the product of ![]() and
and ![]() is equal to the product of
is equal to the product of ![]() and
and ![]() .
.
Problem 9
The sequences of positive integers ![]() and
and ![]() are an increasing arithmetic sequence and an increasing geometric sequence, respectively. Let
are an increasing arithmetic sequence and an increasing geometric sequence, respectively. Let ![]() . There is an integer
. There is an integer ![]() such that
such that ![]() and
and ![]() . Find
. Find ![]() .
.
Problem 10
Triangle ![]() is inscribed in circle
is inscribed in circle ![]() . Points
. Points ![]() and
and ![]() are on side
are on side ![]() with
with ![]() . Rays
. Rays![]() and
and ![]() meet
meet ![]() again at
again at ![]() and
and ![]() (other than
(other than ![]() ), respectively. If
), respectively. If ![]() and
and ![]() , then
, then ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 11
For positive integers ![]() and
and ![]() , define
, define ![]() to be
to be ![]() -nice if there exists a positive integer
-nice if there exists a positive integer ![]() such that
such that ![]() has exactly
has exactly ![]() positive divisors. Find the number of positive integers less than
positive divisors. Find the number of positive integers less than ![]() that are neither
that are neither ![]() -nice nor
-nice nor ![]() -nice.
-nice.
Problem 12
The figure below shows a ring made of six small sections which you are to paint on a wall. You have four paint colors available and you will paint each of the six sections a solid color. Find the number of ways you can choose to paint the sections if no two adjacent sections can be painted with the same color.
![[asy] draw(Circle((0,0), 4)); draw(Circle((0,0), 3)); draw((0,4)--(0,3)); draw((0,-4)--(0,-3)); draw((-2.598, 1.5)--(-3.4641, 2)); draw((-2.598, -1.5)--(-3.4641, -2)); draw((2.598, -1.5)--(3.4641, -2)); draw((2.598, 1.5)--(3.4641, 2)); [/asy]](http://latex.artofproblemsolving.com/f/b/8/fb859ada9b08ae3472e7ba1166edc94baaacc34a.png)
Problem 13
Beatrix is going to place six rooks on a ![]() chessboard where both the rows and columns are labeled
chessboard where both the rows and columns are labeled ![]() to
to ![]() ; the rooks are placed so that no two rooks are in the same row or the same column. The
; the rooks are placed so that no two rooks are in the same row or the same column. The ![]() of a square is the sum of its row number and column number. The
of a square is the sum of its row number and column number. The ![]() of an arrangement of rooks is the least value of any occupied square.The average score over all valid configurations is
of an arrangement of rooks is the least value of any occupied square.The average score over all valid configurations is ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
Problem 14
Equilateral ![]() has side length
has side length ![]() . Points
. Points ![]() and
and ![]() lie outside the plane of
lie outside the plane of ![]() and are on opposite sides of the plane. Furthermore,
and are on opposite sides of the plane. Furthermore, ![]() , and
, and ![]() , and the planes of
, and the planes of ![]() and
and ![]() form a
form a ![]() dihedral angle (the angle between the two planes). There is a point
dihedral angle (the angle between the two planes). There is a point ![]() whose distance from each of
whose distance from each of ![]() and
and ![]() is
is ![]() . Find
. Find ![]() .
.
Problem 15
For ![]() let
let ![]() and
and ![]() . Let
. Let ![]() be positive real numbers such that
be positive real numbers such that  and
and  . The maximum possible value of
. The maximum possible value of ![]() , where
, where ![]() and
and ![]() are relatively prime positive integers. Find
are relatively prime positive integers. Find ![]() .
.
108
107
265
180
182
275
840
728
262
043
749
732
371
450
863
Solution
1.
Let ![]() be the common ratio, where
be the common ratio, where ![]() . We then have
. We then have ![]() . We now have, letting, subtracting the 2 equations,
. We now have, letting, subtracting the 2 equations, ![]() , so we have
, so we have ![]() or
or ![]() , which is how much Betty had. Now we have
, which is how much Betty had. Now we have ![]() , or
, or ![]() , or
, or ![]() , which solving for
, which solving for ![]() gives
gives ![]() , since
, since ![]() , so Alex had
, so Alex had ![]() peanuts.
peanuts.
2.
Let ![]() be the probability that it rains on Sunday given that it doesn't rain on Saturday. We then have
be the probability that it rains on Sunday given that it doesn't rain on Saturday. We then have ![]()
![]() . Therefore, the probability that it doesn't rain on either day is
. Therefore, the probability that it doesn't rain on either day is ![]() . Therefore, the probability that rains on at least one of the days is
. Therefore, the probability that rains on at least one of the days is ![]() , so adding up the
, so adding up the ![]() numbers, we have
numbers, we have ![]() .
.
3.
First, we get rid of logs by taking powers: ![]() ,
, ![]() , and
, and ![]() . Adding all the equations up and using the
. Adding all the equations up and using the ![]() property, we have
property, we have ![]() , so we have
, so we have ![]() . Solving for
. Solving for ![]() by substituting
by substituting ![]() for
for ![]() in each equation, we get
in each equation, we get ![]() , so adding all the absolute values we have
, so adding all the absolute values we have ![]() .
.
4.
By counting the number of green cubes ![]() different ways, we have
different ways, we have ![]() , or
, or ![]() . Notice that there are only
. Notice that there are only ![]() possible colors for unit cubes, so for each of the
possible colors for unit cubes, so for each of the ![]() layers, there are
layers, there are ![]() yellow cubes, and similarly there are
yellow cubes, and similarly there are ![]() red cubes in each of the
red cubes in each of the ![]() layers. Therefore, we have
layers. Therefore, we have ![]() and
and ![]() . We check a few small values of
. We check a few small values of ![]() and solve for
and solve for ![]() , checking
, checking ![]() gives
gives ![]() with a volume of
with a volume of ![]() ,
, ![]() gives
gives ![]() with a volume of
with a volume of ![]() , and
, and ![]() gives
gives ![]() , with a volume of
, with a volume of ![]() . Any higher
. Any higher ![]() will
will ![]() , so therefore, the minimum volume is
, so therefore, the minimum volume is ![]() .
.
5.
Note that by counting the area in 2 ways, the first altitude is ![]() . By similar triangles, the common ratio is
. By similar triangles, the common ratio is ![]() for reach height, so by the geometric series formula, we have
for reach height, so by the geometric series formula, we have  . Multiplying by the denominator and expanding, the equation becomes
. Multiplying by the denominator and expanding, the equation becomes ![]() . Cancelling
. Cancelling ![]() and multiplying by
and multiplying by ![]() yields
yields ![]() , so
, so ![]() and
and ![]() . Checking for Pythagorean triples gives
. Checking for Pythagorean triples gives ![]() and
and ![]() , so
, so ![]()
6.
Note that all the coefficients of odd-powered terms is an odd number of odd degree terms multiplied together, and all coefficients of even-powered terms have an even number of odd degree terms multiplied together. Since every odd degree term is negative, and every even degree term is positive, the sum is just equal to ![]() , so the desired answer is
, so the desired answer is ![]() .
.
7.
Letting ![]() and
and ![]() , we have
, we have ![]() by CS inequality. Also, since
by CS inequality. Also, since ![]() , the angles that each square cuts another are equal, so all the triangles are formed by a vertex of a larger square and
, the angles that each square cuts another are equal, so all the triangles are formed by a vertex of a larger square and ![]() adjacent vertices of a smaller square are similar. Therefore, the areas form a geometric progression, so since
adjacent vertices of a smaller square are similar. Therefore, the areas form a geometric progression, so since ![]() , we have the maximum area is
, we have the maximum area is ![]() (the areas of the squares from largest to smallest are
(the areas of the squares from largest to smallest are ![]() forming a geometric progression).
forming a geometric progression).
The minimum area is ![]() (every square is half the area of the square whose sides its vertices touch), so the desired answer is
(every square is half the area of the square whose sides its vertices touch), so the desired answer is ![]() .
.
8.
Note that the prime factorization of the product is ![]() . Ignoring overcounting, by stars and bars there are
. Ignoring overcounting, by stars and bars there are ![]() ways to choose how to distribute the factors of
ways to choose how to distribute the factors of ![]() , and
, and ![]() ways to distribute the factors of the other primes, so we have
ways to distribute the factors of the other primes, so we have ![]() ways. However, some sets have
ways. However, some sets have ![]() numbers that are the same, namely the ones in the form
numbers that are the same, namely the ones in the form ![]() and
and ![]() , which are each counted
, which are each counted ![]() times, and each other set is counted
times, and each other set is counted ![]() times, so the desired answer is
times, so the desired answer is ![]() .
.
9.
Since all the terms of the sequences are integers, and 100 isn't very big, we should just try out the possibilities for ![]() . When we get to
. When we get to ![]() and
and ![]() , we have
, we have ![]() and
and ![]() , which works, therefore, the answer is
, which works, therefore, the answer is ![]() .
.
10.
![[asy] import cse5; pathpen = black; pointpen = black; pointfontsize = 9; size(8cm); pair A = origin, B = (13,0), P = (4,0), Q = (7,0), T = B + 5 dir(220), C = IP(circumcircle(A,B,T),Line(T,Q,-0.1,10)), S = IP(circumcircle(A,B,C),Line(C,P,-0.1,10)); Drawing(A--B--C--cycle); D(circumcircle(A,B,C),rgb(0,0.6,1)); DrawPathArray(C--S^^C--T,rgb(1,0.4,0.1)); DrawPathArray(A--S^^B--T,rgb(0,0.4,0)); D(S--T,rgb(1,0.2,0.4)); D("A",A,dir(215)); D("B",B,dir(330)); D("P",P,dir(240)); D("Q",Q,dir(240)); D("T",T,dir(290)); D("C",C,dir(120)); D("S",S,dir(250)); MP("4",(A+P)/2,dir(90)); MP("3",(P+Q)/2,dir(90)); MP("6",(Q+B)/2,dir(90)); MP("5",(B+T)/2,dir(140)); MP("7",(A+S)/2,dir(40)); [/asy]](http://latex.artofproblemsolving.com/f/6/0/f603df291461fa6afd0563d94abdc2644aeb97ec.png)
Let ![]() ,
, ![]() , and
, and ![]() . Note that since
. Note that since ![]() we have
we have ![]() , so by the Ratio Lemma
, so by the Ratio Lemma![]() Similarly, we can deduce
Similarly, we can deduce ![]() and hence
and hence ![]() .
.
Now Law of Sines on ![]() ,
, ![]() , and
, and ![]() yields
yields![]() Hence
Hence![]() so
so![]() Hence
Hence ![]() and the requested answer is
and the requested answer is ![]() .
.
Edit: Note that the finish is much simpler. Once you get, ![]() , so
, so ![]() .
.
11.
We claim that an integer ![]() is only
is only ![]() -nice if and only if
-nice if and only if ![]() . By the number of divisors formula, the number of divisors of
. By the number of divisors formula, the number of divisors of ![]() is
is ![]() . Since all the
. Since all the ![]() s are divisible by
s are divisible by ![]() in a perfect
in a perfect ![]() power, the only if part of the claim follows. To show that all numbers
power, the only if part of the claim follows. To show that all numbers ![]() are
are ![]() -nice, write
-nice, write ![]() . Note that
. Note that ![]() has the desired number of factors and is a perfect kth power. By PIE, the number of positive integers less than
has the desired number of factors and is a perfect kth power. By PIE, the number of positive integers less than ![]() that are either
that are either ![]() or
or ![]() is
is ![]() , so the desired answer is
, so the desired answer is ![]() .
.
12.
Choose a section to start coloring. Assume, WLOG, that this section is color ![]() . We proceed coloring clockwise around the ring. Let
. We proceed coloring clockwise around the ring. Let ![]() be the number of ways to color the first
be the number of ways to color the first ![]() sections (proceeding clockwise) such that the last section has color
sections (proceeding clockwise) such that the last section has color ![]() . In general (except for when we complete the coloring), we see that
. In general (except for when we complete the coloring), we see that![]() i.e.,
i.e., ![]() is equal to the number of colorings of
is equal to the number of colorings of ![]() sections that end in any color other than
sections that end in any color other than ![]() . Using this, we can compute the values of
. Using this, we can compute the values of ![]() in the following table.
in the following table.

Note that ![]() because then
because then ![]() adjacent sections are both color
adjacent sections are both color ![]() . We multiply this by
. We multiply this by ![]() to account for the fact that the initial section can be any color. Thus the desired answer is
to account for the fact that the initial section can be any color. Thus the desired answer is ![]() .
.
13.
We casework to find the number of ways to get each possible score. Note that the lowest possible score is ![]() and the highest possible score is
and the highest possible score is ![]() . Let the bijective function
. Let the bijective function ![]() denote the row number of the rook for the corresponding column number.
denote the row number of the rook for the corresponding column number.
For a score of ![]() , we must have
, we must have ![]() , and we can arrange the rest of the function however we want, so there are
, and we can arrange the rest of the function however we want, so there are ![]() ways.
ways.
For a score of ![]() , we must have either
, we must have either ![]() or
or ![]() , and we can arrange the rest of the rooks however we want, so by PIE the number of ways is
, and we can arrange the rest of the rooks however we want, so by PIE the number of ways is ![]() .
.
For a score of ![]() , we must have
, we must have ![]() ,
, ![]() , or
, or ![]() . If
. If ![]() , we just don't want
, we just don't want ![]() , if
, if ![]() , we don't want
, we don't want ![]() , or if
, or if ![]() , we don't want
, we don't want ![]() , otherwise we can arrange the function however we like. If at least
, otherwise we can arrange the function however we like. If at least ![]() of the values rooks have a value of
of the values rooks have a value of ![]() , we can arange the rest of the rooks however we like, so there are
, we can arange the rest of the rooks however we like, so there are ![]() by PIE.
by PIE.
If the score is ![]() , then we have either
, then we have either ![]() ,
, ![]() ,
, ![]() , or
, or ![]() . If we have the first case, we don't want
. If we have the first case, we don't want ![]() ,
, ![]() , or
, or ![]() , so by PIE the number of bad cases is
, so by PIE the number of bad cases is ![]() . If we have the second case, then we don't want
. If we have the second case, then we don't want ![]() ,
, ![]() , or
, or ![]() , so similarly there are
, so similarly there are ![]() bad cases. Therefore, there are a total of
bad cases. Therefore, there are a total of ![]() good cases for each one. The number of ways to get
good cases for each one. The number of ways to get ![]() is
is ![]() because we don't want
because we don't want ![]() , the number of ways to get
, the number of ways to get ![]() is
is ![]() ways because we don't want
ways because we don't want ![]() , the number of ways to get
, the number of ways to get ![]() is
is ![]() ways because we don't want
ways because we don't want ![]() , and the number of ways to get
, and the number of ways to get ![]() is
is ![]() ways because we don't want
ways because we don't want ![]() . The number of ways to get at least
. The number of ways to get at least ![]() cases satisfied is
cases satisfied is ![]() because we can arrange the remaining rooks however we like, and the number of ways to get all
because we can arrange the remaining rooks however we like, and the number of ways to get all ![]() cases satisfied is
cases satisfied is ![]() ways because we can arrange the remaining rooks however we like, so by PIE we have
ways because we can arrange the remaining rooks however we like, so by PIE we have ![]() ways to get a score of
ways to get a score of ![]() .
.
The only way to get a score of ![]() is to have all the rooks run on the antidiagonal. Therefore, the number of ways to get a sum of
is to have all the rooks run on the antidiagonal. Therefore, the number of ways to get a sum of ![]() is
is ![]() .
.
Thus, the expected sum is ![]() , so the desired answer is
, so the desired answer is ![]() .
.
14.
The inradius of ![]() is
is ![]() and the circumradius is
and the circumradius is ![]() . Now, consider the line perpendicular to plane
. Now, consider the line perpendicular to plane ![]() through the circumcenter of
through the circumcenter of ![]() . Note that
. Note that ![]() must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since
must lie on that line to be equidistant from each of the triangle's vertices. Also, note that since ![]() are collinear, and
are collinear, and ![]() , we must have
, we must have ![]() is the midpoint of
is the midpoint of ![]() . Now, Let
. Now, Let ![]() be the circumcenter of
be the circumcenter of ![]() , and
, and ![]() be the foot of the altitude from
be the foot of the altitude from ![]() to
to ![]() . We must have
. We must have ![]() . Setting
. Setting ![]() and
and ![]() , assuming WLOG
, assuming WLOG ![]() , we must have
, we must have  . Therefore, we must have
. Therefore, we must have ![]() . Also, we must have
. Also, we must have ![]() by the Pythagorean theorem, so we have
by the Pythagorean theorem, so we have ![]() , so substituting into the other equation we have
, so substituting into the other equation we have ![]() , or
, or ![]() . Since we want
. Since we want ![]() , the desired answer is
, the desired answer is ![]() .
.
15.
Note that Substituting this into the second equation and collecting
Substituting this into the second equation and collecting ![]() terms, we find
terms, we find![\[\sum_{i=1}^{216}\frac{x_i^2}{1-a_i}=\frac{1}{215}.\]](http://latex.artofproblemsolving.com/d/4/3/d4313463f68af4d0981c85ce35494272c0d286ea.png) Conveniently,
Conveniently,  so we find
so we find![\[\left(\sum_{i=1}^{216} 1-a_i\right)\left(\sum_{i=1}^{216}\frac{x_i^2}{1-a_i}\right)=1=\left(\sum_{i=1}^{216} x_i\right)^2.\]](http://latex.artofproblemsolving.com/6/a/4/6a4227127147ab66814e5f3ce3b4911a5f21b9cc.png) This is the equality case of the Cauchy-Schwarz Inequality, so
This is the equality case of the Cauchy-Schwarz Inequality, so ![]() for some constant
for some constant ![]() . Summing these equations and using the facts that
. Summing these equations and using the facts that  and
and  , we find
, we find ![]() and thus
and thus ![]() . Hence the desired answer is
. Hence the desired answer is ![]() .
.
报名及辅导请联系
最新学术活动真题解析免费领,高能讲座不间断

翰林AIME课程体系流程图
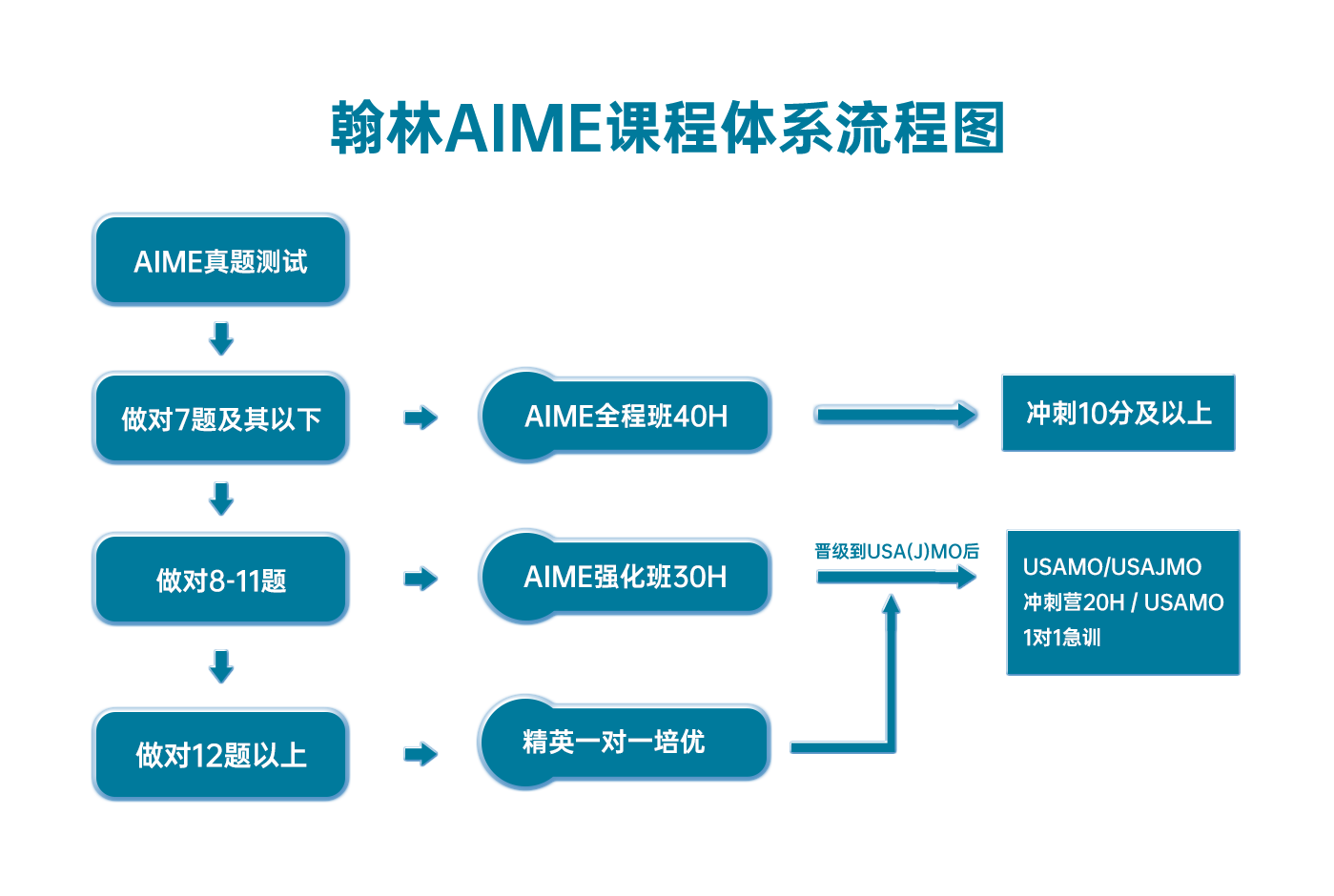
完整版真题资料可以底部二维码免费领取↓↓↓
[products columns="2" orderby="title" order="" ids="26004, 720, 719, 718"]

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









