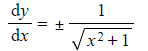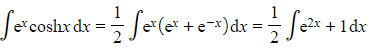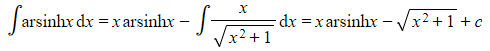Edexcel A Level Further Maths: Core Pure:复习笔记4.1.4 Differentiating & Integrating Hyperbolic Functions
Differentiating Hyperbolic Functions
What are the derivatives of the hyperbolic functions?
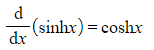
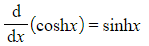
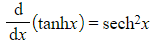
- These are given in the formulae booklet
- You can prove them by differentiating the definitions involving e
- Notice that they are similar to the derivatives of the circular trig functions
- Be careful of the difference between the derivatives of cosx and coshx
- One involves a negative sign and the other does not
- Be careful of the difference between the derivatives of cosx and coshx
How do I differentiate expressions involving hyperbolic functions?
- The following differentiation skills may be required
- Chain rule
- Product rule
- Quotient rule
- Implicit differentiation
- Questions may involve showing or proving given results or finding unknown constants
- It is common that derivatives can be written in terms of the original function
- This is due to the derivative of ex also being ex giving rise to the repetition of terms
What are the derivatives of the inverse hyperbolic functions?
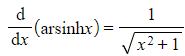
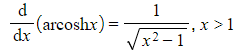
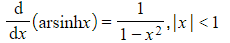
- These are given in the formulae booklet
How do I prove or show the derivatives of the inverse hyperbolic functions?
- Use the same method for differentiating any inverse function
- STEP 1
Write x in terms of y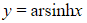
can be written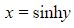 
- STEP 2
Differentiate with respect to y - STEP 3
Write the derivative in terms of x - STEP 4
Take the reciprocal - STEP 5
Use the graph to determine whether it is positive of negative- The graph of
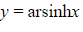has a positive gradient everywhere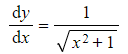 
- The graph of
Exam Tip
- It is usually easier to differentiate hyperbolic functions using the “trig style” standard results but if you are stuck you can try using their exponential form from the definitions
Worked Example
a) Given that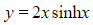 
, show that 
.
, show that .
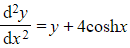b) Given that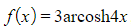 
, show that 
where 
and 
are constants to be found.
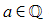, show that where and 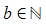are constants to be found.
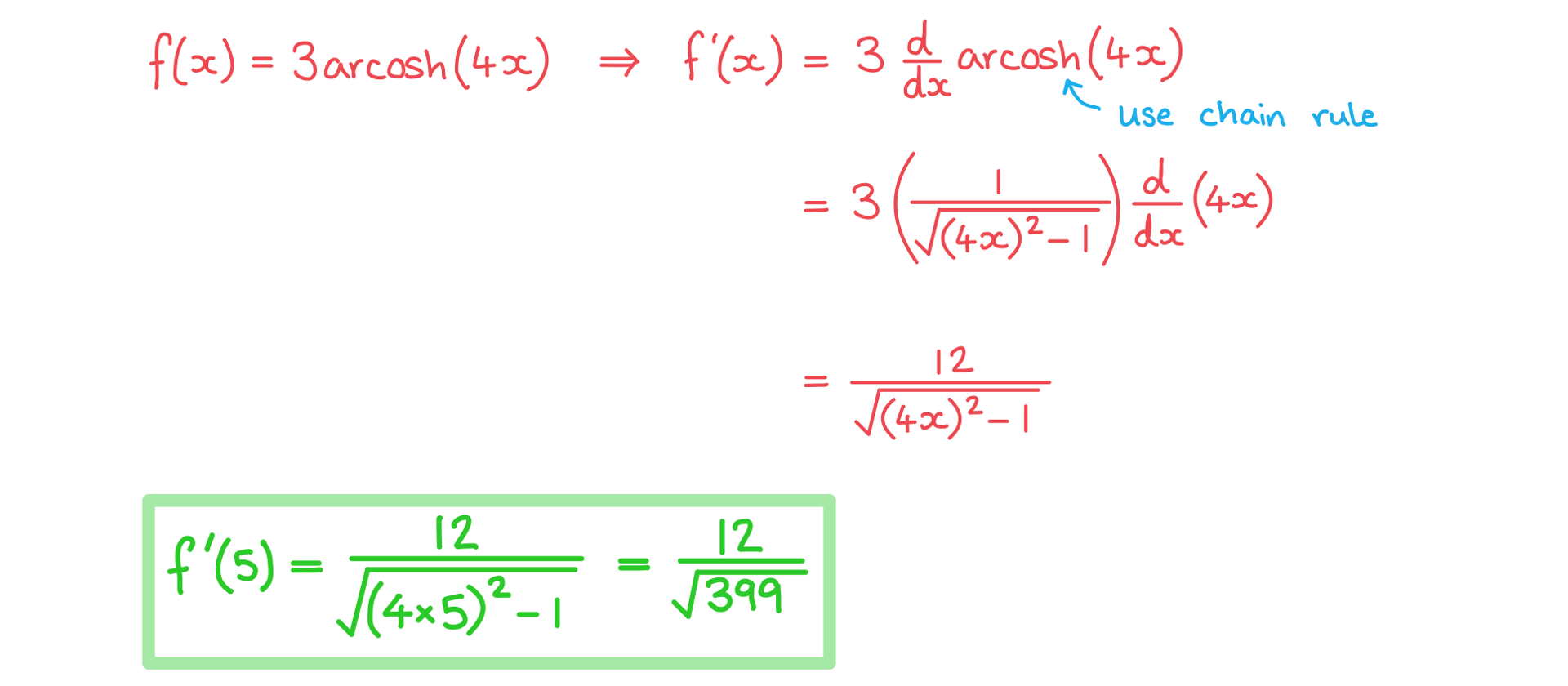
Integrating Hyperbolic Functions
What are the integrals of the hyperbolic functions?
- These are the reverse results of the derivatives, remembering “+c” of course!
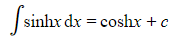
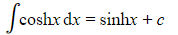
- These are given in the integration section of the formulae booklet
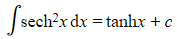
- This can be deduced from the differentiation section of the formulae booklet
- There is also the integral of tanhx
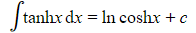
- This is given in the integration section of the formulae booklet
- It can be shown using the substitution
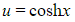
- Since cosh ≥ 1 for all values of x so there is no need for the modulus signs that usually accompany integrals involving ln
How do I integrate expressions involving or resulting in hyperbolic functions?
- The following integration skills may be required
- Definite integration, area under a curve
- Reverse chain rule (‘adjust’ and ‘compensate’)
- Substitution
- Integration by parts
- Hyperbolic identities may be required to rewrite an expression into an integrable form
- For products involving ex and a hyperbolic function use the definition involving ex and e-x for the hyperbolic function to write everything in terms of exponentials
How do I integrate expressions involving inverse hyperbolic functions?
- To integrate inverse hyperbolic functions you would use integration by parts using the same technique as integrating lnx
- Write the functions as a product with 1
- e.g.
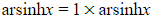
- e.g.
- Differentiate the inverse function and integrate 1 when integrating by parts
- Write the functions as a product with 1
Exam Tip
- Be aware of what is given in the formula booklet
- Practise using it to find integrals
- The results for hyperbolic functions and the inverse circular trig functions are listed together so try not to get confused
- If you can't spot a relevant hyperbolic identity then using exponentials can make the expression easier and quicker to integrate
Worked Example
Find the following integrals:
a)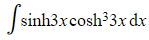
b)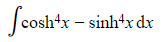
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
