- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记4.1.1 Hyperbolic Functions & Graphs
Hyperbolic Functions & Graphs
What are the definitions of the hyperbolic functions?
- Hyperbolic sine
![]()
-
- This can be pronounced "shine" or "sinch"
- Hyperbolic cosine
![]()
-
- This can be pronounced "cosh"
- Hyperbolic tangent

-
- This can be pronounced "than" or "tanch"
What are the graphs of the hyperbolic functions and their key features?
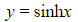
- Domain:
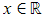
- Range:
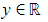
- Non-stationary point of inflection at (0, 0)
- Its shape is similar to the graph of
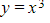
- Domain:

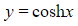
- Domain:
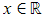
- Range:
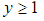
- Global minimum point at (0, 1)
- Its shape is similar to the graph of
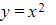
- Domain:

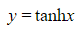
- Domain:
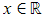
- Range:
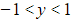
- Non-stationary point of inflection at (0, 0)
- Asymptotes at y=1 and y=-1
- Its shape is similar to the graph of
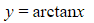
- Domain:
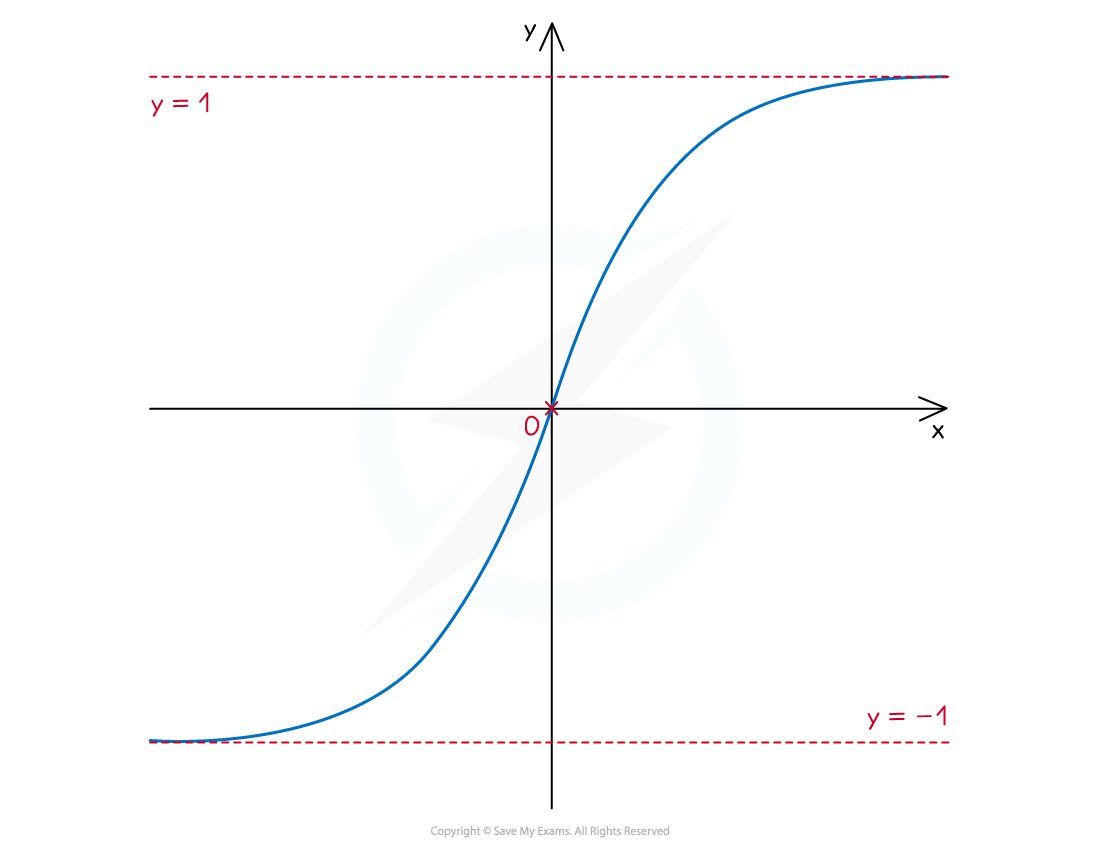
What other features of the hyperbolic functions and graphs do I need to know?
- The graphs of y=sinhx and y=tanhx have rotational symmetry about the origin
- This means that
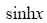 and are therefore odd functions
and are therefore odd functions
- This means that
- The graph of y=coshx is symmetrical in the y-axis
- This means that
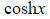 is therefore an even function
is therefore an even function
- This means that
What may I be asked to do with hyperbolic functions and their graphs?
- Sketch graphs and transformations
- e.g.
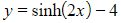
- Write as a transformation of
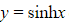 and apply the transformations in the correct order
and apply the transformations in the correct order
- Write as a transformation of
- Where possible label the key features of the transformed graph
- Intersections with the coordinate axes
- Equations of any asymptotes
- Coordinates of any turning points
- e.g.
- Find exact values
- e.g. Find the exact value of
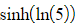
- Use the definitions to write in terms of e
- Use
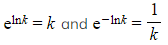
- e.g. Find the exact value of
Exam Tip
- When using a calculator make sure you use sinh, cosh and tanh and NOT sin, cos and tan
- Questions asking for values in exact form are often easier “to see” without a calculator, using the definitions of sinh and cosh, rather than trying to type in a complicated expression with e and ln
Worked Example
a) Find the exact values of
(i)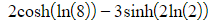
(ii)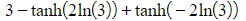

b) Sketch the graph of 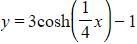 , labelling any points where the graph crosses the coordinate axes and any turning points.
, labelling any points where the graph crosses the coordinate axes and any turning points.
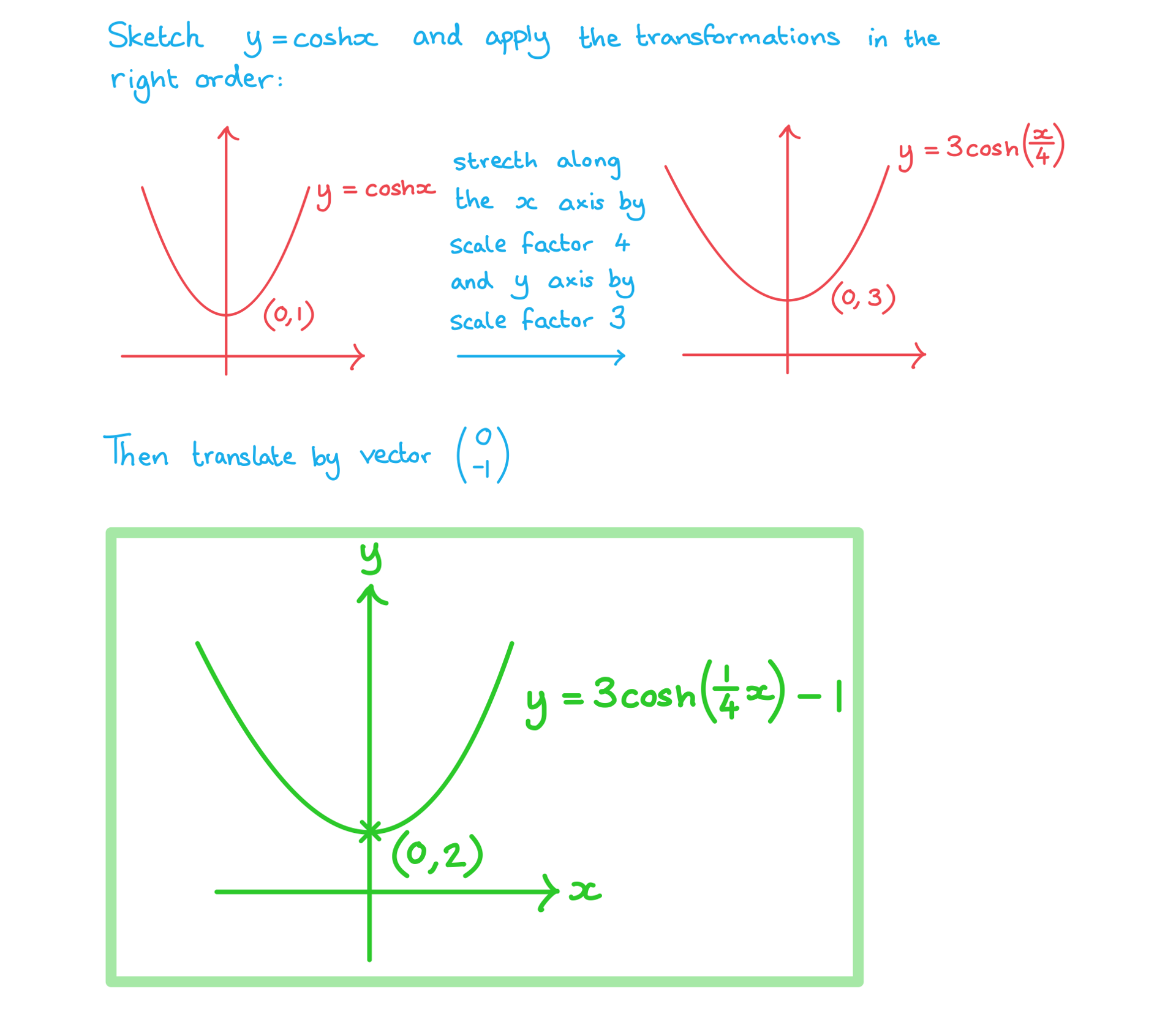
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









