- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记3.3.1 Maclaurin Series
Maclaurin Series
What is a Maclaurin Series?
- A Maclaurin series is a way of representing a function as an infinite sum of increasing integer powers of
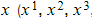 etc.)
etc.)
- If all of the infinite number of terms are included, then the Maclaurin series is exactly equal to the original function
- If we truncate (i.e., shorten) the Maclaurin series by stopping at some particular power of
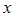 , then the Maclaurin series is only an approximation of the original function
, then the Maclaurin series is only an approximation of the original function
- A truncated Maclaurin series will always be exactly equal to the original function for
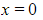
- In general, the approximation from a truncated Maclaurin series becomes less accurate as the value of
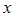 moves further away from zero
moves further away from zero - The accuracy of a truncated Maclaurin series approximation can be improved by including more terms from the complete infinite series
- So, for example, a series truncated at the
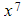 term will give a more accurate approximation than a series truncated at the
term will give a more accurate approximation than a series truncated at the 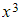 term
term
- So, for example, a series truncated at the
How do I find the Maclaurin series of a function ‘from first principles’?
- Use the general Maclaurin series formula
![]()
- This formula is in your exam formula booklet
- STEP 1: Find the values of
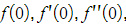 etc. for the function
etc. for the function
-
- An exam question will specify how many terms of the series you need to calculate (for example, “up to and including the term in
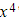 ”)
”) - You may be able to use your calculator to find these values directly without actually having to find all the necessary derivatives of the function first
- An exam question will specify how many terms of the series you need to calculate (for example, “up to and including the term in
- STEP 2: Put the values from Step 1 into the general Maclaurin series formula
- STEP 3: Simplify the coefficients as far as possible for each of the powers of
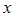
Is there a connection Maclaurin series expansions and binomial theorem series expansions?
- Yes there is!
- For a function like
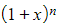 the binomial theorem series expansion is exactly the same as the Maclaurin series expansion for the same function
the binomial theorem series expansion is exactly the same as the Maclaurin series expansion for the same function
- So unless a question specifically tells you to use the general Maclaurin series formula, you can use the binomial theorem to find the Maclaurin series for functions of that type
- Or if you’ve forgotten the binomial series expansion formula for
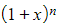 where
where 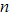 is not a positive integer, you can find the binomial theorem expansion by using the general Maclaurin series formula to find the Maclaurin series expansion
is not a positive integer, you can find the binomial theorem expansion by using the general Maclaurin series formula to find the Maclaurin series expansion
Worked Example
Use the Maclaurin series formula to find the Maclaurin series for 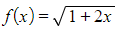 up to and including the term in
up to and including the term in 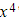 .
.

Maclaurin Series of Standard Functions
Is there an easier way to find the Maclaurin series for standard functions?
- Yes there is!
- The following Maclaurin series expansions of standard functions are contained in your exam formula booklet:
- Unless a question specifically asks you to derive a Maclaurin series using the general Maclaurin series formula, you can use those standard formulae from the exam formula booklet in your working
Maclaurin Series of Compound Functions
How can I find the Maclaurin series for a composite function?
- A composite function is a ‘function of a function’ or a ‘function within a function’
- For example sin(2x) is a composite function, with 2x as the ‘inside function’ which has been put into the simpler ‘outside function’ sin x
- Similarly
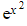 is a composite function, with
is a composite function, with 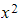 as the ‘inside function’ and
as the ‘inside function’ and 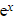 as the ‘outside function’
as the ‘outside function’
- To find the Maclaurin series for a composite function:
- STEP 1: Start with the Maclaurin series for the basic ‘outside function’
- Usually this will be one of the ‘standard functions’ whose Maclaurin series are given in the exam formula booklet
- STEP 2: Substitute the ‘inside function’ every place that x appears in the Maclaurin series for the ‘outside function’
- So for sin(2x), for example, you would substitute 2x everywhere that x appears in the Maclaurin series for sin x
- STEP 3: Expand the brackets and simplify the coefficients for the powers of x in the resultant Maclaurin series
- STEP 1: Start with the Maclaurin series for the basic ‘outside function’
- This method can theoretically be used for quite complicated ‘inside’ and ‘outside’ functions
- On your exam, however, the ‘inside function’ will usually not be more complicated than something like kx (for some constant k) or xn (for some constant power n)
How can I find the Maclaurin series for a product of two functions?
- To find the Maclaurin series for a product of two functions:
- STEP 1: Start with the Maclaurin series of the individual functions
- For each of these Maclaurin series you should only use terms up to an appropriately chosen power of x (see the worked example below to see how this is done!)
- STEP 2: Put each of the series into brackets and multiply them together
- Only keep terms in powers of x up to the power you are interested in
- STEP 3: Collect terms and simplify coefficients for the powers of x in the resultant Maclaurin series
- STEP 1: Start with the Maclaurin series of the individual functions
Worked Example
a) Find the Maclaurin series for the function 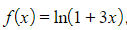 , up to and including the term in
, up to and including the term in 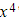 .
.

b) Find the Maclaurin series for the function 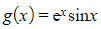 , up to and including the term in
, up to and including the term in 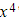 .
.

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1