Edexcel A Level Further Maths: Core Pure:复习笔记3.1.2 Linear Transformations of Roots
Linear Transformations of Roots
What is a Linear Transformation?
- A linear transformation can be expressed as
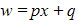where:
- w is the new root
- x is the original root
- p and q are constants
- If you perform a linear transformation on a polynomial equation, the transformed equation’s roots will be linked directly to the original roots
- You can think of this as a translation and/or a stretch of the polynomial and its roots
How do I find the new transformed polynomial?
- STEP 1
Rewrite the transformation as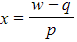 
- STEP 2
Make the substitution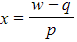 into the original polynomial - STEP 3
Expand and multiply by a constant to make all the coefficients integers (if necessary or desirable) and swap the w back for an x in your final answer - Remember that your solution is not unique. Multiplying the entire polynomial by a constant will produce a different polynomial, but will not affect the roots
Exam Tip
- Check the question to see if you are required to expand and simplify your final answer or not, as it can be time consuming!
- If you are required to expand and simplify, make use of the binomial expansion to make the process much quicker
- Use your calculator’s polynomial solver to check the solutions of the original equation and your new equation, to make sure they are related to each other as described
Worked Example
The cubic equation 
has roots 
Find a polynomial equation with roots:
a)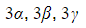
b)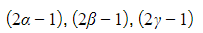
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
