- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记2.1.2 Determinants of Matrices
Determinant of a 2x2 Matrix
What is a determinant?
- The determinant is a numerical value (positive or negative) calculated from the elements in a matrix and is used to find the inverse of a matrix
- You can only find the determinant of a square matrix
- The method for finding the determinant of a
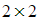 matrix is given by:
matrix is given by:
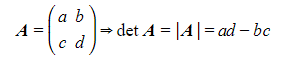
Worked Example
Consider the matrix 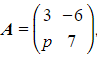 , where
, where ![]() is a constant. Given that
is a constant. Given that ![]() , find the value of
, find the value of![]() .
.
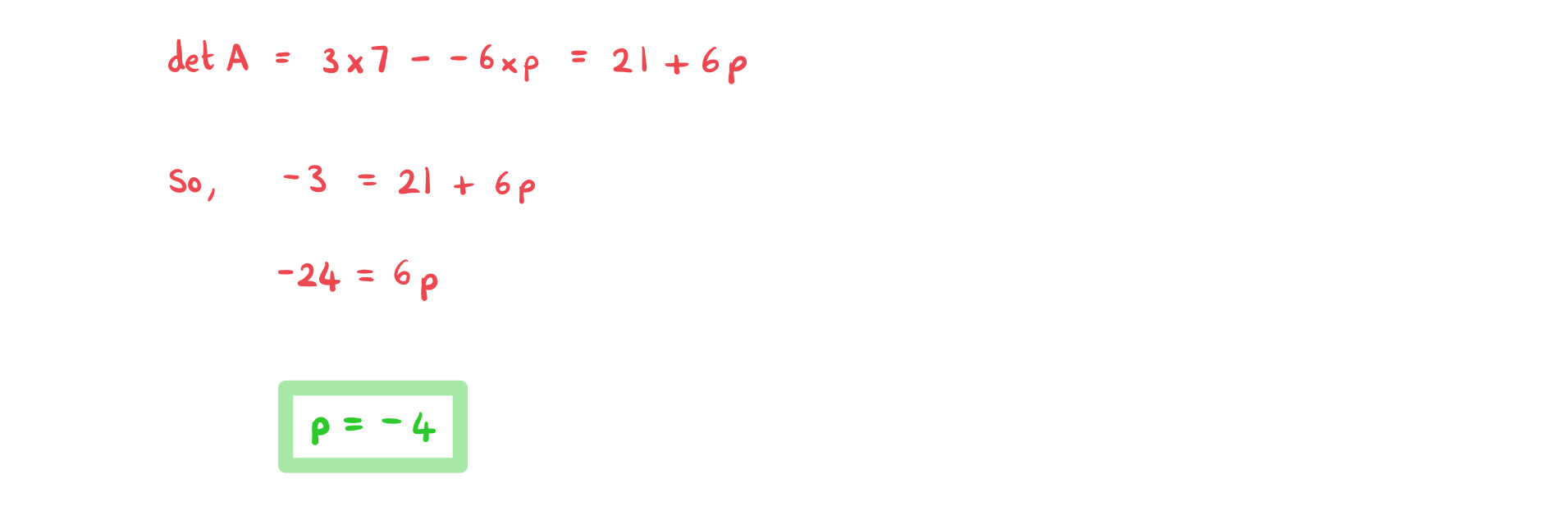
Determinant of a 3x3 Matrix
What is the minor of an element in a 3x3 matrix?
- For any element in a 3x3 matrix, the minor is the determinant of the 2x2 matrix created by crossing out the row and column containing that element
- For the matrix
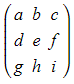
- The minor of the element a would be found by:
- crossing out the first row and first column
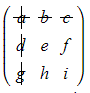
- finding the determinant of the remaining 2x2 matrix
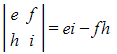
- crossing out the first row and first column
- The minor of the element f would be found by:
- crossing out the second row and third column
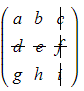
- finding the determinant of the remaining 2x2 matrix
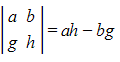
- crossing out the second row and third column
- The minor of the element a would be found by:
How do I find the determinant of a 3x3 matrix?
- Finding the determinant of a 3x3 matrix is best explained using an example
- STEP 1
Select any row or column in the matrix- e.g. Selecting Row 2 of
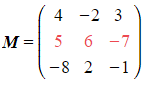
- e.g. Selecting Row 2 of
- STEP 2
Use the matrix of signs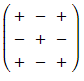 to find the row or column that corresponds to the row or column selected in Step 1
to find the row or column that corresponds to the row or column selected in Step 1
- e.g.
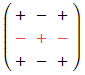 Row 2 was selected so “- + -“ will be needed
Row 2 was selected so “- + -“ will be needed
- e.g.
- STEP 3
Multiply each element in the selected row or column by its minor and use the corresponding signs form the matrix of signs to determine whether to add or subtract each product- e.g.
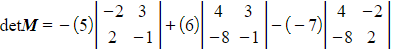
- e.g.
- STEP 4
Evaluate the minors and calculate the determinant- e.g.
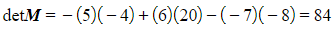
- Check the answer using a calculator with a matrix feature
- e.g.
Exam Tip
- In general, you can use the top row to find the determinant
- this will save having to recall the matrix of signs, it will always be “+ - +”
- and allow you to quickly jump from Step 1 to Step 4 in the method above
- the matrix of signs is still needed for finding the inverse of a 3x3 matrix
- Using a row or column that contains a 0 can speed up the process
- Do use the matrix mode on your calculator where possible
- Look for any notes on questions about using/not using “calculator technology”
- Consider the number of marks a question or part is worth
Worked Example
Let 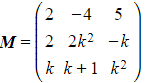 where k is a positive integer.
where k is a positive integer.
a) Find, in terms of k, the determinant of  .
.

b) Given that 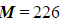 , find the value of k.
, find the value of k.

Properties of Determinants
What are the properties of determinants of matrices?
- The determinant of an identity matrix is
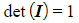
- The determinant of a zero matrix is
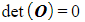
- When finding the determinant of a multiple of a matrix or the product of two matrices:
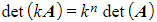 (for a
(for a 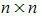 matrix)
matrix)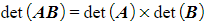
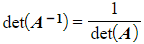
- If
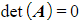 then A is singular
then A is singular - If
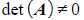 then A is non-singular
then A is non-singular
Worked Example
Consider the matrix 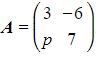 , where
, where ![]() is a constant. Given that
is a constant. Given that
