Edexcel A Level Further Maths: Core Pure:复习笔记1.2.4 Roots of Complex Numbers
Roots of Complex Numbers
How do I find the square root of a complex number?
- The square roots of a complex number will themselves be complex:
- i.e. if
- i.e. if
- We can then square
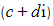and equate it to the original complex number 
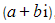, as they both describe 
:
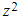- Then expand and simplify:
- As both sides are equal we are able to equate real and imaginary parts:
- Equating the real components:
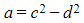(1) - Equating the imaginary components:
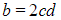(2)
- Equating the real components:
- These equations can then be solved simultaneously to find the real and imaginary components of the square root
- In general, we can rearrange (2) to make
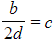and then substitute into (1) - This will lead to a quartic equation in terms of d; which can be solved by making a substitution to turn it into a quadratic
- In general, we can rearrange (2) to make
- The values of
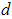can then be used to find the corresponding values of 
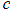, so we now have both components of both square roots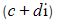 
- Note that one root will be the negative of the other root
- g.
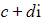and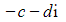 
- g.
How do I use de Moivre’s Theorem to find roots of a complex number?
- De Moivre’s Theorem states that a complex number in modulus-argument form can be raised to the power of n by
- Raising the modulus to the power of n and multiplying the argument by n
- When in modulus-argument (polar) form de Moivre’s Theorem can then be used to find the roots of a complex number by
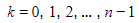
- Recall that adding 2π to the argument of a complex number does not change the complex number
- Therefore we must consider how different arguments will give the same result
- Taking the nth root of the modulus and dividing the argument by n
- If
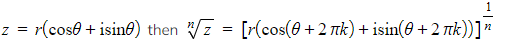
- This can be rewritten as
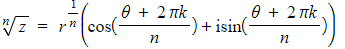
- This can be written in exponential (Euler’s) form as
- For
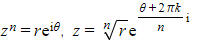
- For
- The nth root of complex number will have n roots with the properties:
- The five roots of a complex number raised to the power 5 will create a regular pentagon on an Argand diagram
- The eight roots of a complex number raised to the power 8 will create a regular octagon on an Argand diagram
- The n roots of a complex number raised to the power n will create a regular n-sided polygon on an Argand diagram
- The modulus is
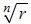for all roots - There will be n different arguments spaced at equal intervals on a circle centred about the origin
- This creates some geometrically beautiful results
Exam Tip
- de Moivre's theorem makes finding roots of complex numbers very easy, but you must be confident converting from Cartesian form into Polar and Euler's form first
- You can use your calculator to convert between forms
Worked Example
a) Find the square roots of 5 + 12i, giving your answers in the form a + bi.
b) Solve the equation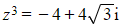 
giving your answers in the form r (cosθ + isinθ).
giving your answers in the form r (cosθ + isinθ).
Roots on an Argand Diagram
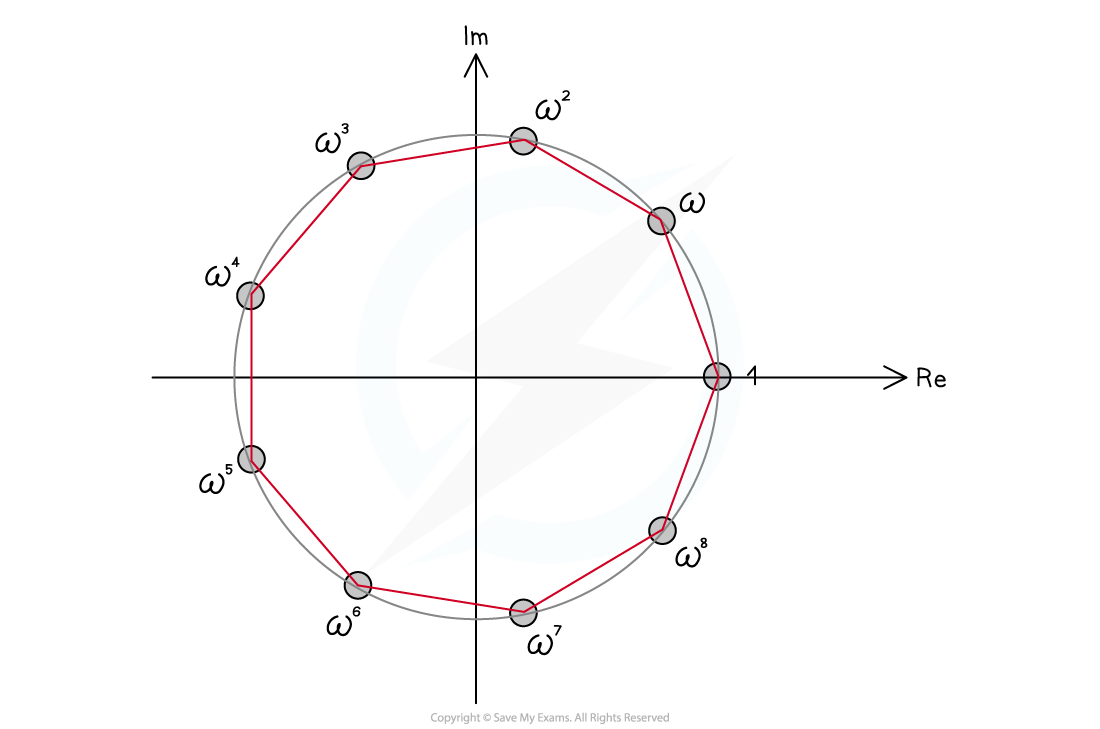
What are roots of unity?
- Roots of unity are solutions to the equation
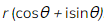where n is a positive integer - For the equation
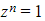there are n roots of unity
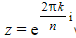where k = 0, 1, 2, …, n-1
- This is given in the formula booklet
- These can be written 1, ω, ω², …, ωn-1
- Where
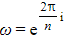
- Where
- The sum of the roots of unity is zero
- They can be used to find all the roots of the equation
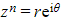
- Find one root normally
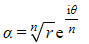
- Then the n distinct roots can be found by multiplying α by each root of unity
- α, αω, αω², …, αωn-1
- Find one root normally
What are the geometric properties of roots of complex numbers?
- The n roots of any non-zero complex number
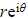lie on a circle on an Argand diagram
- The centre will be the origin
- The radius will be
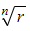
- The n roots of unity lie on the unit circle centred about the origin
- Regular polygons can be created by joining consecutive roots of a complex number with straight lines
How can I use roots of unity to solve geometric problems?
- Roots of unity can be used to solve problems involving regular polygons centred about the origin
- Coordinates of vertices (x, y) can be considered as complex numbers x + yi
- If you know one vertex (x, y) you can find the others by multiplying the complex number representing the given vertex by each root of unity
- x + yi, (x + yi)ω, (x + yi)ω², …, (x + yi)ωn-1
- If you write the vertex using exponential form
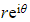it can make the multiplications easier - Then you can just add
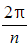to the argument to get the next vertex
- Write all vertices in Cartesian form to get the coordinates
Exam Tip
- You can use your calculator to convert between polar and cartesian forms which may speed up your working
- Just be aware of questions that may ask you to not use “calculator technology” where you need to show full working (but can still use calculator to check!)
Worked Example
An equilateral triangle has its centre at the origin of a Cartesian plane. One of its vertices is at the point 
. Find the coordinates of the other two vertices.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
