Edexcel A Level Further Maths: Core Pure:复习笔记1.1.3 Modulus & Argument
Argand Diagrams - Basics
What is an Argand diagram?
- An Argand diagram is a geometrical way to represent complex numbers as either a point or a vector in two-dimensional space
- We can represent the complex number
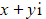by the point with cartesian coordinate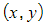
- We can represent the complex number
- The real component is represented by points on the x-axis, called the real axis, Re
- The imaginary component is represented by points on the y-axis, called the imaginary axis, Im
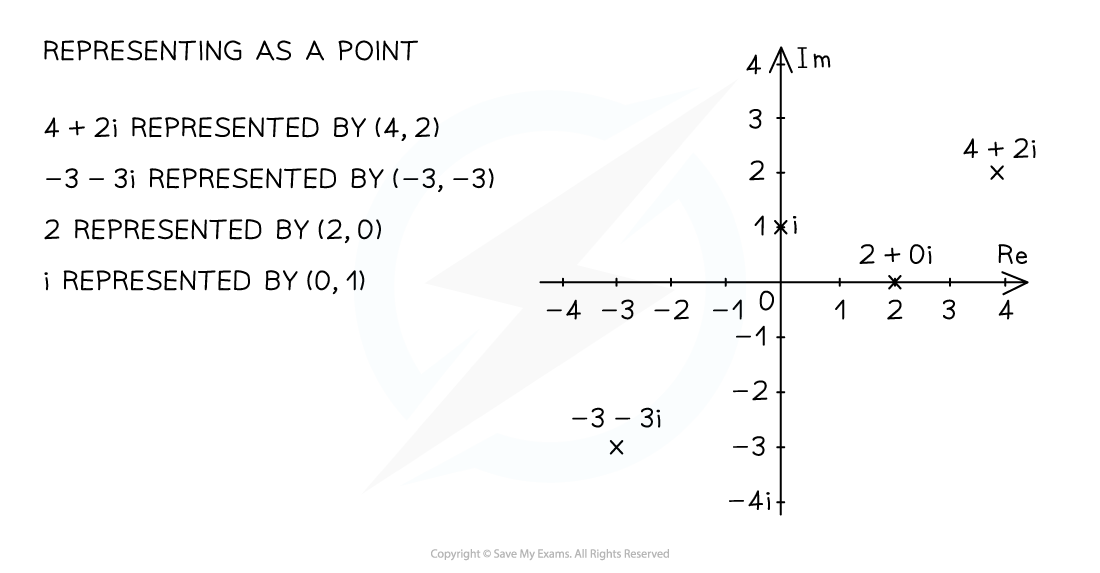
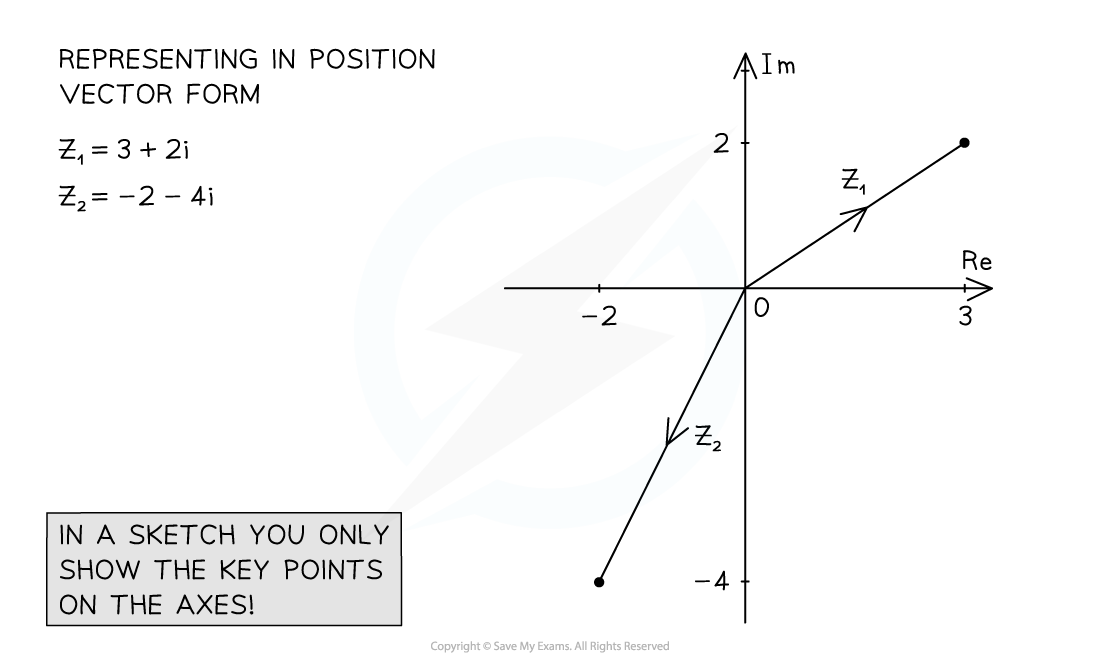
- You may be asked to show roots of an equation in an Argan diagram
- First solve the equation
- Draw a quick sketch, only adding essential information to the axes
- Plot the points and label clearly
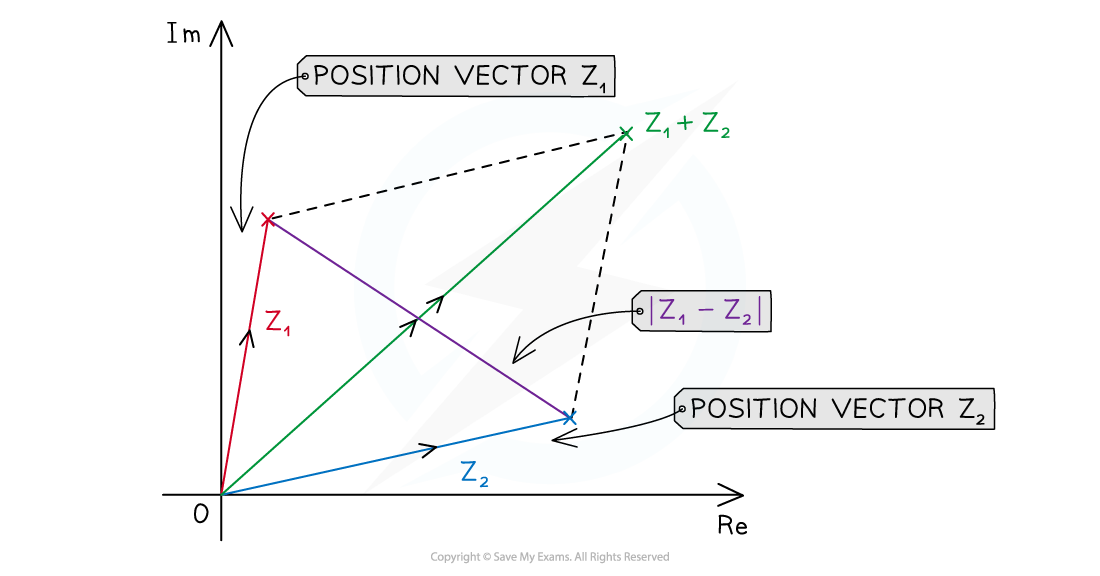
How can I use an Argand diagram to visualise |z1 + z2| and |z1 - z2|?
- Plot two complex numbers z1 and z2
- Draw a line from the origin to each complex number
- Form a parallelogram using the two lines as two adjacent sides
- The modulus of their sum |z1 + z2| will be the length of the diagonal of the parallelogram starting at the origin
- The modulus of their difference |z1 - z2| will be the length of the diagonal between the two complex numbers
Worked Example
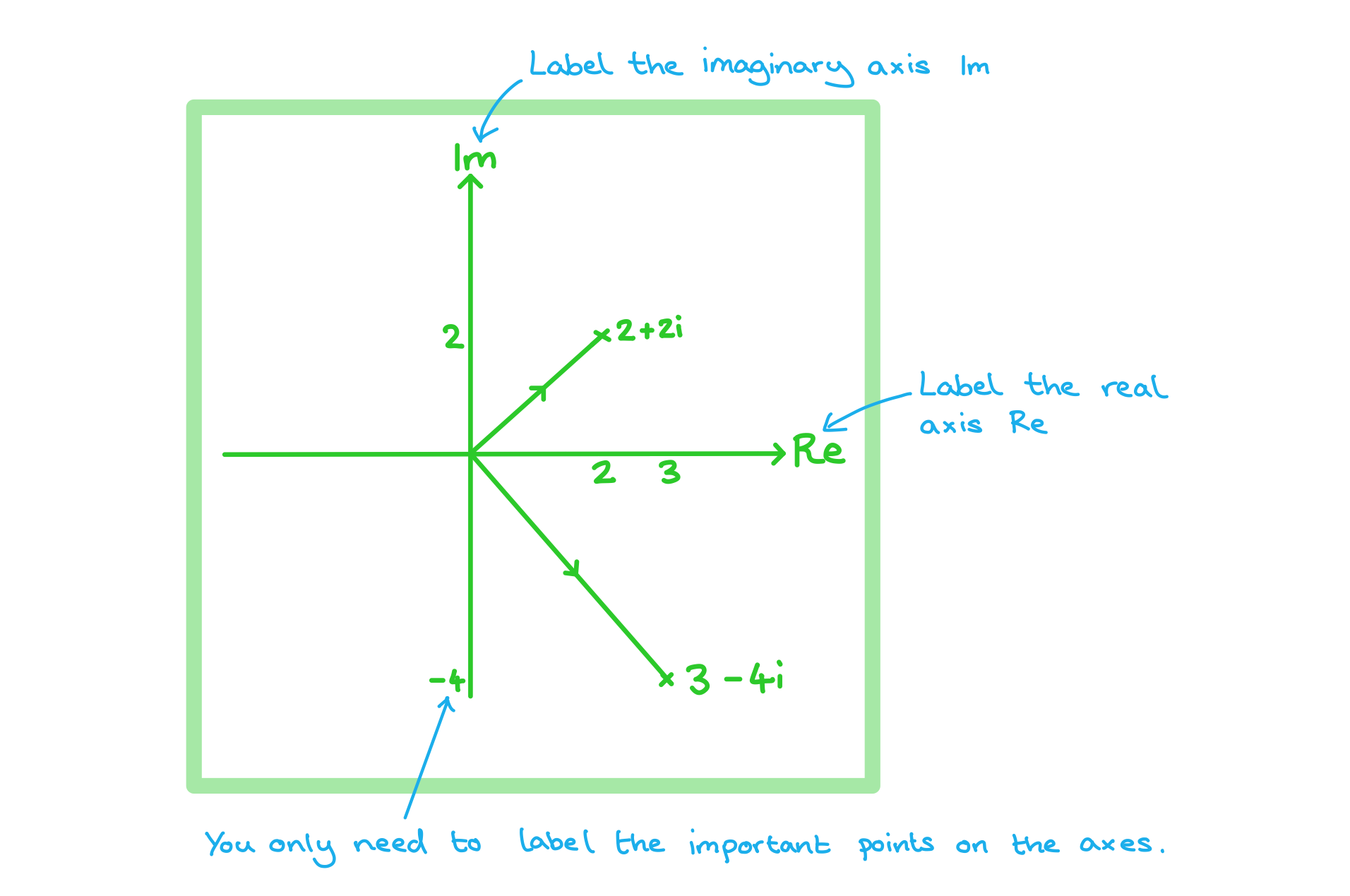
a) Plot the complex numbers z1 = 2 + 2i and z2 = 3 – 4i as points on an Argand diagram.
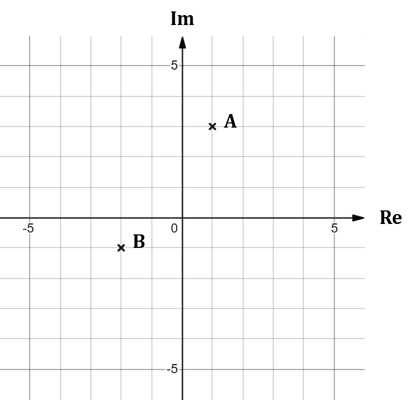
b) Write down the complex numbers represented by the points A and B on the Argand diagram below.
Exam Tip
- When setting up an Argand diagram you do not need to draw a fully scaled axes, you only need the essential information for the points you want to show, this will save a lot of time.
Modulus & Argument
How do I find the modulus of a complex number?
- The modulus of a complex number is its distance from the origin when plotted on an Argand diagram
- The modulus of
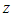is written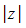 
- If
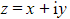, then we can use Pythagoras to show…
- A modulus is always positive
- the modulus is related to the complex conjugate by…
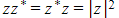
- This is because
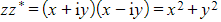
- In general,
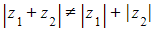
- e.g. both
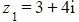and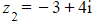 
have a modulus of 5, but 
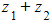simplifies to 
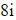which has a modulus of 8
- e.g. both
How do I find the argument of a complex number?
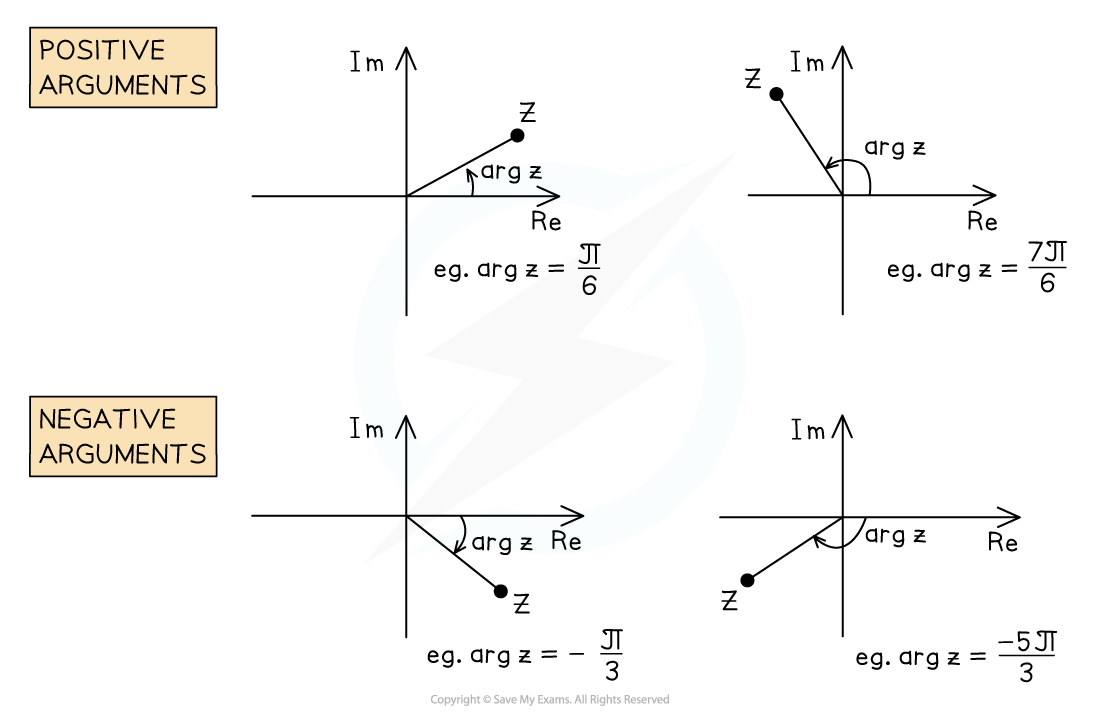
- The argument of a complex number is the anti-clockwise angle that it makes when starting at the positive real axis on an Argand diagram
- Arguments are measured in radians
- Sometimes these can be given exact in terms of
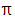
- Sometimes these can be given exact in terms of
- The argument of 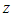is written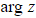
- Arguments can be calculated using right-angled trigonometry
- This involves using the tan ratio plus a sketch to decide whether it is positive/negative and acute/obtuse
- Arguments are usually given in the range
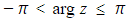
- This is called the principal argument
- Negative arguments are for complex numbers in the third and fourth quadrants
- Occasionally you could be asked to give arguments in the range
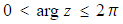
- The argument of zero,
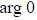is undefined (no angle can be drawn)
Exam Tip
- Always draw a sketch to see which quadrant the complex number is in
Worked Example
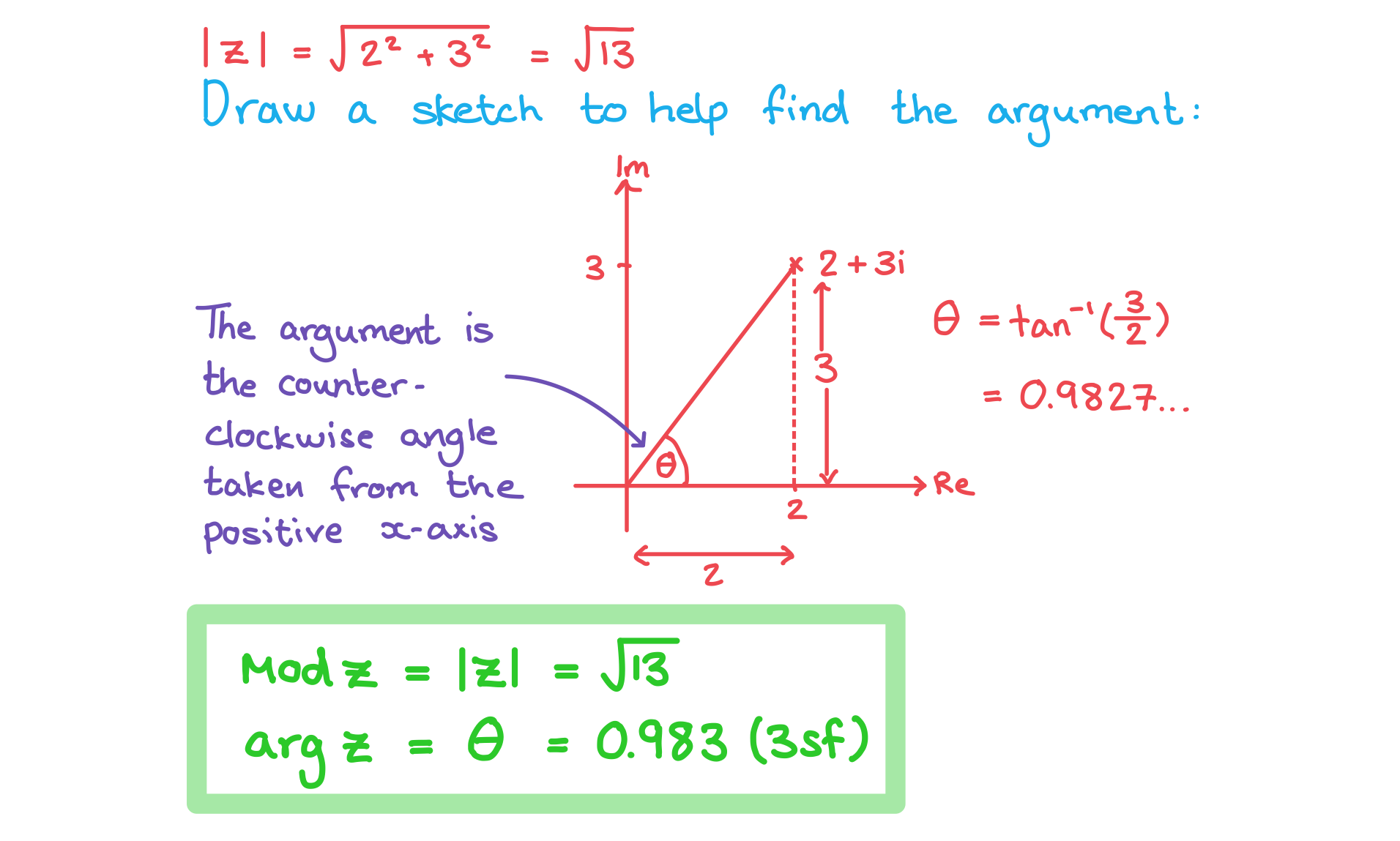
a) Find the modulus and argument of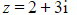 
b) Find the modulus and argument of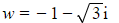 
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
