- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Further Maths: Core Pure:复习笔记1.1.2 Solving Equations with Complex Roots
Solving Quadratic Equations with Complex Roots
What are complex roots?
- Complex numbers provide solutions for quadratic equations which have no real roots
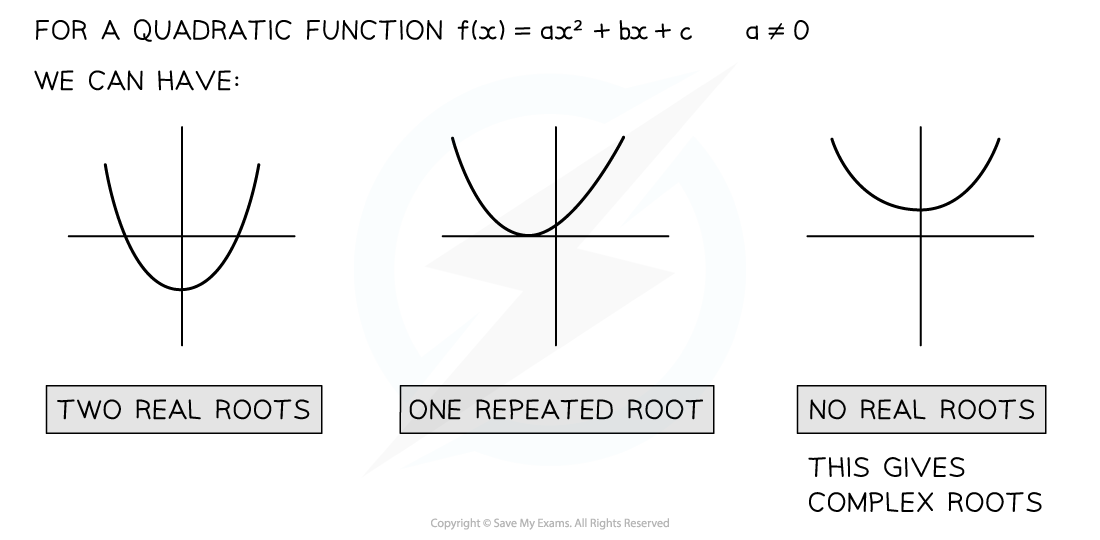
- Complex roots occur when solving a quadratic with a negative discriminant
- This leads to square rooting a negative number
How do we solve a quadratic equation with complex roots?
- We solve an equation with complex roots in the same way we solve any other quadratic equations
- If in the form
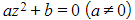 we can rearrange to solve
we can rearrange to solve - If in the form
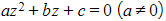 we can complete the square or use the quadratic formula
we can complete the square or use the quadratic formula
- If in the form
- We use the property
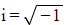 along with a manipulation of surds
along with a manipulation of surds
- When the coefficients of the quadratic equation are real, complex roots occur in complex conjugate pairs
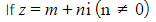 is a root of a quadratic with real coefficients then
is a root of a quadratic with real coefficients then 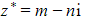 is also a root
is also a root
- When the coefficients of the quadratic equation are non-real, the solutions will not be complex conjugates
- To solve these use the quadratic formula
How do we find a quadratic equation given a complex root?
- We can find the equation of the form
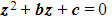 if you are given a complex root in the form
if you are given a complex root in the form 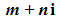
- We know that the complex conjugate
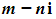 is another root,
is another root, - This means that
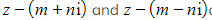 are factors of the quadratic equation
are factors of the quadratic equation - Therefore
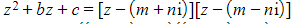
- Writing this as
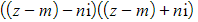 will speed up expanding
will speed up expanding
- Writing this as
- Expanding and simplifying gives us a quadratic equation where b and c are real numbers
- We know that the complex conjugate
Exam Tip
- Once you have your final answers you can check your roots are correct by substituting your solutions back into the original equation.
- You should get 0 if correct! [Note: 0 is equivalent to
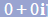 ]
]
Worked Example
a) Solve the quadratic equation z2 - 2z + 5 = 0 and hence, factorise z2 - 2z + 5.

b) Given that one root of a quadratic equation is z = 2 – 3i, find the quadratic equation in the form az2 + bz + c = 0, where a, b, and c ∈ ℝ, a ≠ 0.

Solving Polynomial Equations with Complex Roots
How many roots should a polynomial have?
- We know that every quadratic equation has two roots (not necessarily distinct or real)
- This is a particular case of a more general rule:
- Every polynomial equation, with real coefficients, of degree n has n roots
- The n roots are not necessarily all distinct and therefore we need to count any repeated roots that may occur individually
- From the above rule we can state the following:
- A cubic equation of the form
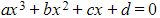 can have either:
can have either:
- 3 real roots
- Or 1 real root and a complex conjugate pair
- A cubic equation of the form
- A quartic equation of the form
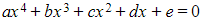 will have one of the following cases for roots:
will have one of the following cases for roots:
- 4 real roots
- 2 real and 2 nonreal (a complex conjugate pair)
- 4 nonreal (two complex conjugate pairs)
- When a real polynomial of any degree has one complex root it will always also have the complex conjugate as a root
How do we solve a cubic equation with complex roots?
- Steps to solve a cubic equation with complex roots
- If we are told that
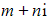 is a root, then we know
is a root, then we know 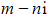 is also a root
is also a root - This means that
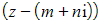 and
and 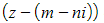 are factors of the cubic equation
are factors of the cubic equation - Multiply the above factors together gives us a quadratic factor of the form
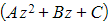
- We need to find the third factor
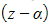
- Multiply the factors and equate to our original equation to get
- If we are told that
![]()
- From there either
- Expand and compare coefficients to find
- Or use polynomial division to find the factor
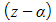
- Expand and compare coefficients to find
- Finally, write your three roots clearly
How do we solve a polynomial of any degree with complex roots?
- When asked to find the roots of any polynomial when we are given one, we use almost the same method as for a cubic equation
- State the initial root and its conjugate and write their factors as a quadratic factor (as above) we will have two unknown roots to find, write these as factors (z - α) and (z - β)
- The unknown factors also form a quadratic factor (z - α)(z - β)
- Then continue with the steps from above, either comparing coefficients or using polynomial division
- If using polynomial division, then solve the quadratic factor you get to find the roots α and β
How do we solve polynomial equations with unknown coefficients?
- Steps to find unknown variables in a given equation when given a root:
- Substitute the given root p + qi into the equation f(z) = 0
- Expand and group together the real and imaginary parts (these expressions will contain our unknown values)
- Solve as simultaneous equations to find the unknowns
- Substitute the values into the original equation
- From here continue using the previously described methods for finding other roots for the polynomial
How do we factorise a polynomial when given a complex root?
- If we are given a root of a polynomial of any degree in the form z = p + qi
- We know that the complex conjugate, z* = p – qi is another root
- We can write (z – (p + qi)) and ( z – (p - qi)) as two linear factors
- Or rearrange into one quadratic factor
- This can be multiplied out with another factor to find further factors of the polynomial
- For higher order polynomials more than one root may be given
- If the further given root is complex then its complex conjugate will also be a root
- This will allow you to find further factors
Exam Tip
- As with solving quadratic equations, we can substitute our solutions back into the original equation to check we get 0
- You can speed up multiplying two complex conjugate factors together by
- rewrite (z – (p + qi))(z – (p - qi)) as ((z – p) - qi))( (z – p) + qi))
- Then ((z – p) - qi))( (z – p) + qi)) = (z - p)2 - (qi)2 = (z - p)2 + q2
Worked Example
Given that one root of a polynomial p(x) = z3 + z2 – 7z + 65 is 2 – 3i, find the other roots.

转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1








