- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Physics:复习笔记13.1 Conditions for Simple Harmonic Motion
Conditions for Simple Harmonic Motion
- Simple harmonic motion (SHM) is a specific type of oscillation
- An oscillation is said to be SHM when:
- The acceleration is proportional to the displacement
- The acceleration is in the opposite direction to the displacement
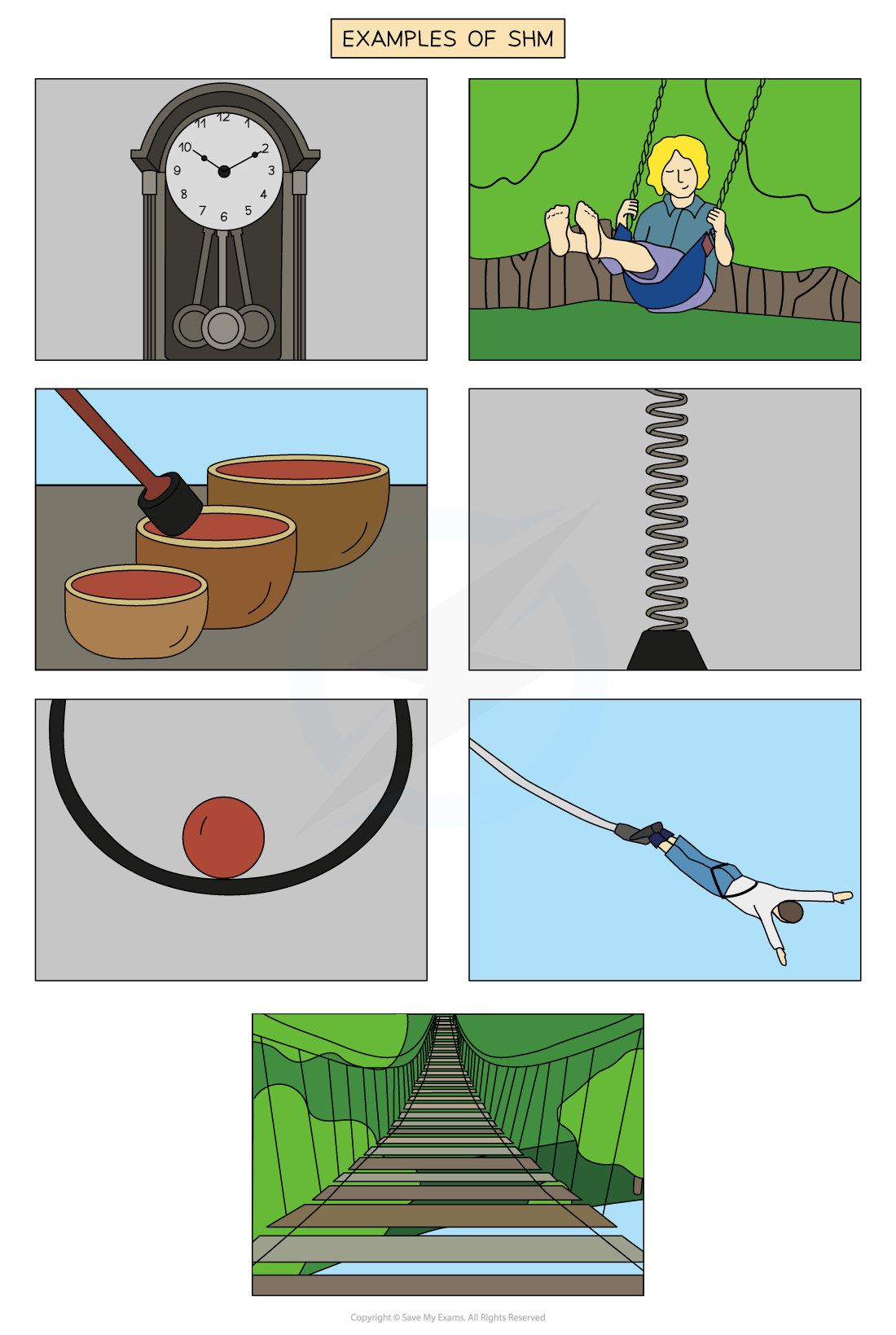
- Examples of oscillators that undergo SHM are:
- The pendulum of a clock
- A mass on a spring
- Guitar strings
- The electrons in alternating current flowing through a wire
- Time period, T:
- The objects swings are periodic, meaning they are repeated in regular intervals according to their frequency or time period
- If an object swings freely it always takes the same time to complete one swing
Restoring force
- When an object is moving in SHM a force, called the restoring force, F, is always trying to return the object back to its equilibrium position.
- The force is proportional to the displacement, x, from that equilibrium position
F = -kx
- Where:
- F is the restoring force
- x is the displacement of the object from the equilibrium position
- k is a constant depending on the system
- the negative sign shows that the acceleration will always be towards the centre of oscillation
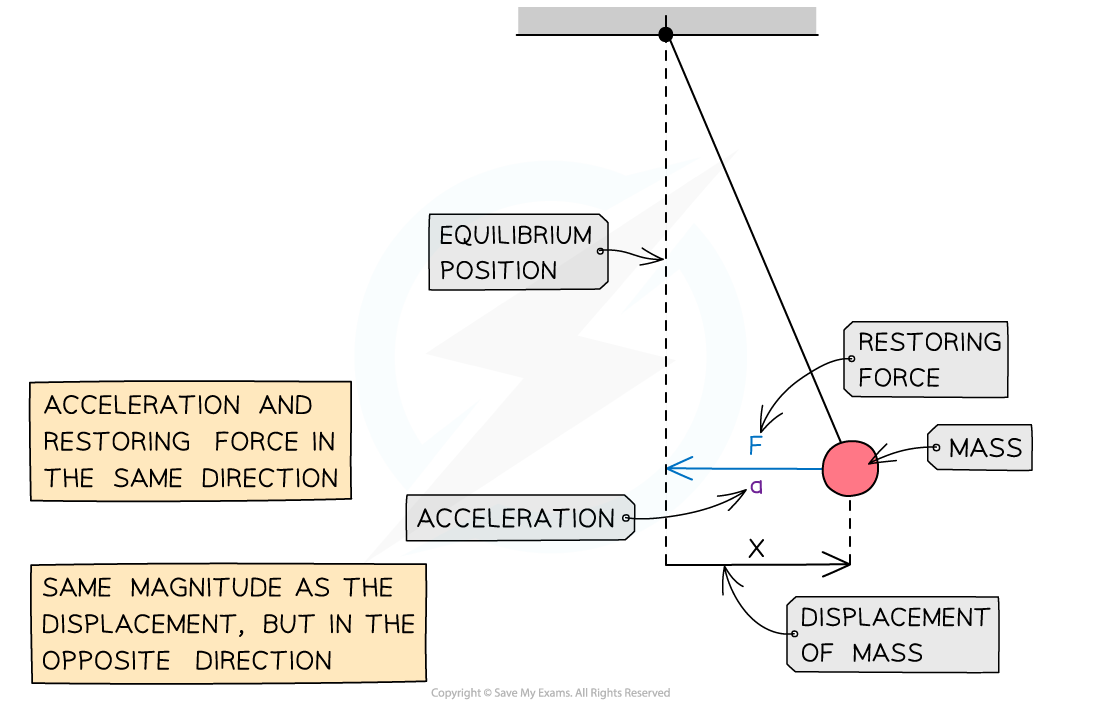
Force, acceleration and displacement of a pendulum in SHM
- This is why a person jumping on a trampoline is not an example of simple harmonic motion:
- The restoring force on the person is not proportional to their distance from the equilibrium position
- When the person is not in contact with the trampoline, the restoring force is equal to their weight, which is constant
- This does not change, even if they jump higher
Worked Example
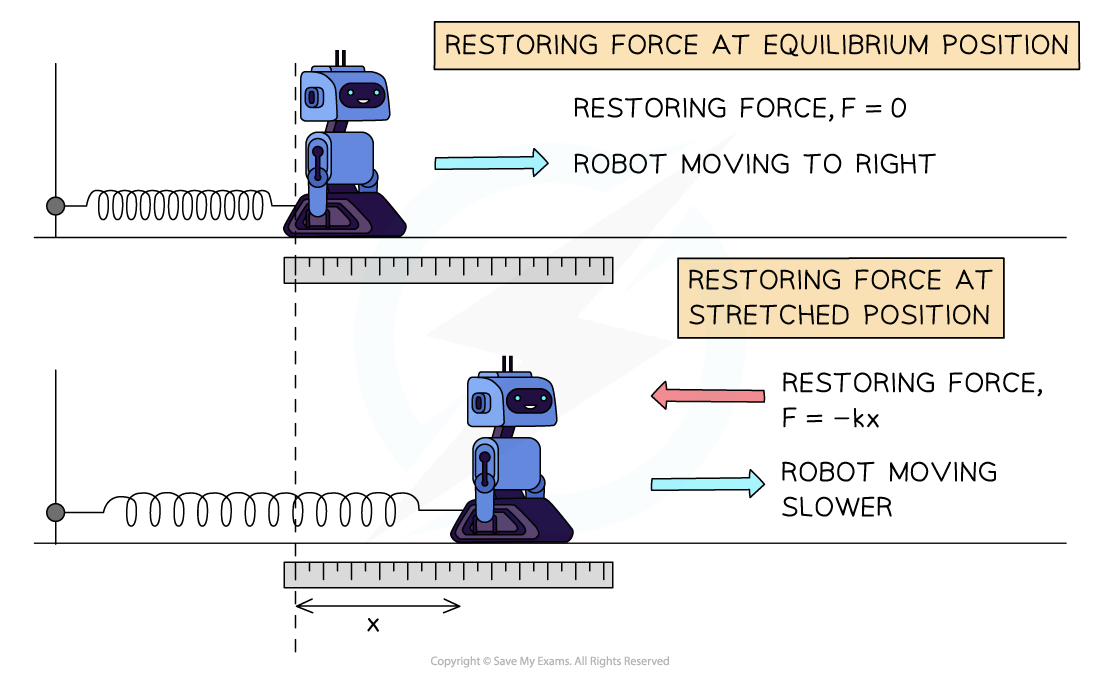
A 200g toy robot is attached to a pole by a spring, with a spring constant of 90 N m-1, and made to oscillate horizontally.
(a) What force will act on the robot when it is at its amplitude position of 5 cm from equilibrium?
(b) How fast will the robot accelerate whilst at this amplitude position?
Part (a)
Step 1: Convert amplitude into m
5 cm = 0.05 m
Step 2: Substitute values into the restoring force equation
F = -kx = -(90) x (0.05) = - 4.5 N
Step 3: Explain the answer
A force of 4.5 newtons will act on the robot, trying to pull it back towards the equilibrium position.
Part (b)
Step 1: Convert mass of robot into kg
200 g = 0.2 kg
Step 2: Substitute values into Newton's second law equation:
F = ma
So, ![]() = -22.5 m s-2
= -22.5 m s-2
Step 3: Explain the answer
The train will decelerate at a rate of 22.5 m s-2 when at this amplitude position
Exam Tip
Even with this topic you must make sure you convert all quantities into standard SI units
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









