- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Physics:复习笔记7.13 Exponential Discharge in a Capacitor
Exponential Discharge in a Capacitor
The Discharge Equation
- When a capacitor discharges through a resistor, the charge stored on it decreases exponentially
- The amount of charge remaining on the capacitor Q after some elapsed time t is governed by the exponential decay equation:
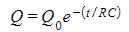
- Where:
- Q = charge remaining (C)
- Q0 = initial charge stored (C)
- e = exponential function
- t = elapsed time (s)
- R = circuit resistance (Ω)
- C = capacitance (F)
Discharge Equation for Potential Difference
- The exponential decay equation for charge can be used to derive a decay equation for potential difference
- Recall the equation for charge Q = CV
- It also follows that the initial charge Q0 = CV0 (where V0 is the initial potential difference)
- Therefore, substituting CV for Q into the original exponential decay equation gives:
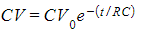
- Cancelling C from both sides gives the exponential decay equation for potential difference V:
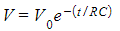
- Where:
- V = potential difference after some time t (V)
- V0 = initial potential difference (V)
- t = elapsed time (s)
- R = resistance (Ω)
- C = capacitance (F)
- This equation shows that the potential difference also decreases exponentially, from some initial value V0
-
Discharge Equation for Current
- The exponential decay equation for potential difference can be used to derive a decay equation for current
- Recall Ohm's law V = IR
- It follows that the initial potential difference V0 = I0R (where I0 is the initial current)
- Therefore, substituting IR for V into the decay equation for potential difference gives:
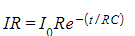
- Cancelling R from both sides gives the exponential decay equation for current I:
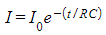
- Where:
- I = current after some time t (A)
- I0 = initial current (A)
- t = elapsed time (s)
- R = resistance (Ω)
- C = capacitance (F)
- This equation shows that the current also decreases exponentially, from some initial value I0
Worked Example
A 10 mF capacitor is fully charged by a 12 V power supply and then discharged through a 1 kΩ resistor.
What is the discharge current after 15 s?
Step 1: Write the known quantities
-
- Initial potential difference V0 = 12 V
- Resistance R = 1 kΩ = 1000 Ω
- Capacitance C = 10 mF = 0.01 F
- Time elapsed = 15 s
Step 2: Determine the initial current I0
-
- Since the initial potential difference is 12 V and the resistance is 1000 Ω, then:
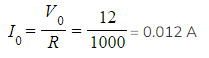
Step 3: Write the decay equation for current
-
- The decay equation for current is:
Step 4: Substitute quantities and calculate the current after 15 s
-
- Substituting quantities gives the following:
I = (0.012) × (e–(15/(1000 × 0.01))
I = (0.012) × (e–1.5)
I = (0.012) × (0.223...)
I = 2.7 × 10–3 A = 2.7 mA
Exam Tip
Remember you can work out initial quantities like current or potential difference or charge using the equations:
- V0 = I0R
- Q0 = CV0
You will then usually have enough information to substitute all necessary values into the decay equations!
Natural Logarithms & Discharge Equations
- The exponential decay equations are not linear
- They can be turned into linear equations by using the natural logarithm function
- Recall the exponential decay equation for charge:
- Dividing both sides by Q0 gives:
- Taking the natural logarithm of both sides 'cancels' the exponential function e, giving:
- This simplifies to:
- Leaving an equation for the natural logarithm of charge Q as:
- This is the equation of a straight line graph, where:
- ln Q is plotted on the y-axis
- t is plotted on the x-axis
- The gradient of the line is therefore equal to –1/RC
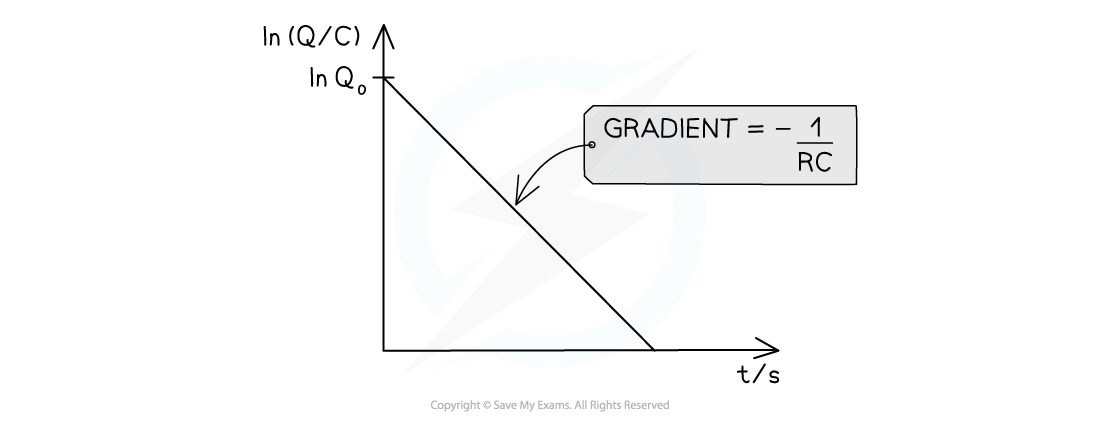
The natural logarithm of the exponential decay curve line arises it to a straight-line graph with a gradient equal to –1/RC
- Following similar steps, the linearised versions of the decay equations for potential difference V is:
- And for current I is:
Worked Example
When a capacitor discharges, the voltage V across it varies with time t. A graph showing the variation of ln V against t is shown for a particular discharging capacitor.
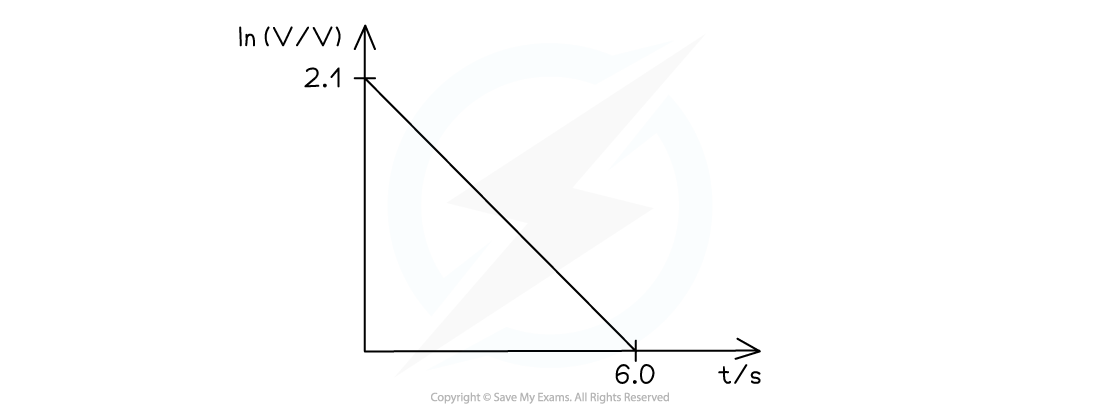
Use the graph to determine the initial voltage across the capacitor.
Step 1: Write the equation for the linearised decay equation for potential difference
-
- The linearised decay equation for potential difference is given by:
Step 2: Interpret the graph given using the linearised equation
-
- The equation says the y-intercept of the straight line is represented by ln V0
Step 3: Use the y-intercept to determine the initial voltage
-
- The y-intercept is equal to 2.1
- Therefore:
ln V0 = 2.1
Step 4: Cancel the natural logarithm using the exponential function:
-
- Raising both sides using the exponential function e 'cancels' the natural logarithm
- This gives:
V0 = e(2.1) = 8.2 V
Exam Tip
You need to know how to derive decay equations for pd and for current from the decay equation for charge, as well as how to use and interpret natural logarithm equations. If you can understand that these natural log equations are linear, because they can plotted as a graph in the form y = mx + c, then you are well set for exam questions on this topic! Remember:
- The gradient of the straight line is given by -1/RC
- The y-intercept of the line represents ln Q0 or ln V0 or ln I0
转载自savemyexams

早鸟钜惠!翰林2025暑期班课上线

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1