Edexcel A Level Physics:复习笔记7.10 Energy Stored by a Capacitor
Energy Stored by a Capacitor
- When charging a capacitor, the power supply 'pushes' electrons to one of the metal plates
- It therefore does work on the electrons and electrical energy becomes stored on the plates
- The power supply 'pulls' electrons off of the other metal plate, attracting them to the positive terminal
- This leaves one side positively charged, while the other side becomes negatively charged
- Hence, in this way, charge is 'stored' by the capacitor
- Gradually, this stored charge builds up
- Adding more electrons to the negative plate at first is relatively easy since there is little repulsion
- As the charge of the negative plate increases, i.e., becomes more negatively charged, the force of repulsion between the electrons on the plate and the new electrons being pushed onto it increases
- This means a greater amount of work must be done to increase the charge on the negative plate or in other words:
The potential difference across the capacitor increases as the amount of charge increases
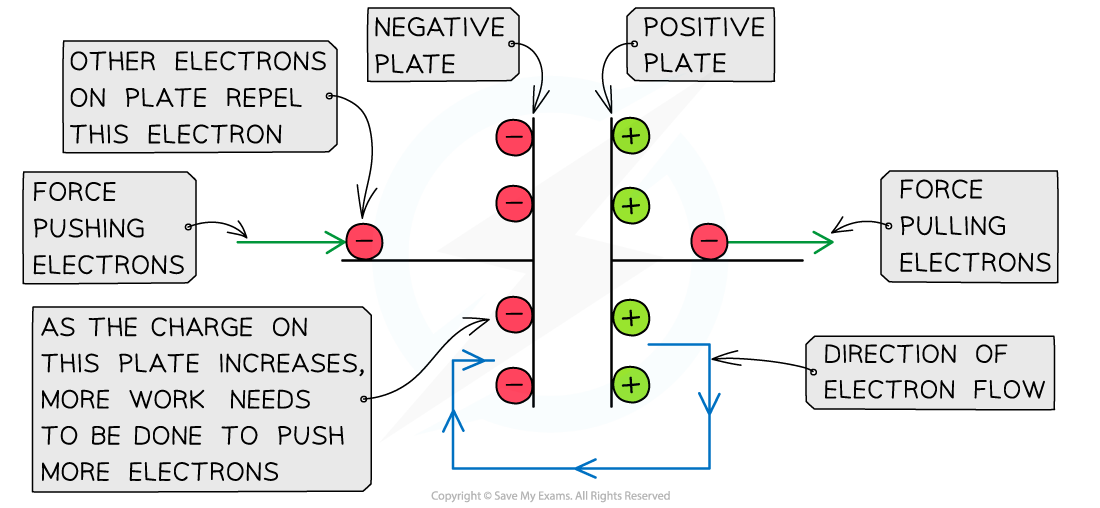
As the charge on the negative plate builds up, more work needs to be done to add more charge
Alternative Equations for Energy Stored
- The energy stored by a capacitor is given by:
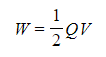
- Substituting the charge Q with the capacitance equation Q = CV, the energy stored can also be calculated by the following equation:
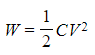
- By substituting the potential difference V, the energy stored can also be defined in terms of just the charge stored Q and the capacitance, C:
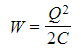
Worked Example
Calculate the change in the energy stored in a capacitor of capacitance 1500 μF when the potential difference across the capacitor changes from 10 V to 30 V.
Step 1: Write down the equation for energy stored, in terms of C and V and list the known values
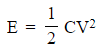
Capacitance, C = 1500μF
Final p.d, V2 = 30 V
Initial p.d V1 =10 V
Step 2: The change in energy stored in proportional to the change in p.d
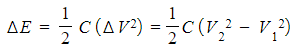
Step 3: Substitute in the values
Exam Tip
Energy stored or work done are used interchangeably (and sometimes written as E or W as shown above). You should be comfortable linking the two equivalent ideas - the energy stored in the capacitor is equal to the work done on it, by the power supply which charges it. Make sure you can apply each of the three equations given above!
Area Under a Potential Difference-Charge Graph
- The charge stored Q on the capacitor is given by the equation Q = CV
- Therefore, the charge stored Q is directly proportional to the potential difference across the plates V
- The graph of charge against potential difference is therefore a straight line graph through the origin
- The gradient of the graph represents the capacitance C, which is a constant
- The electrical (potential) energy stored in the capacitor can be determined from the area under the potential-charge graph which is equal to the area of a right-angled triangle:
Area = 
× base × height
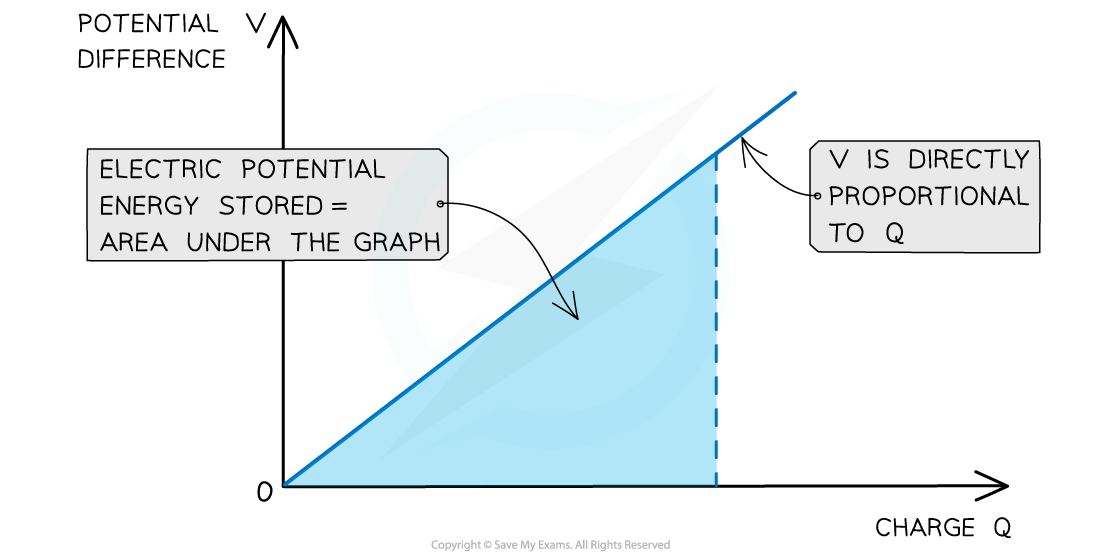
The area under a potential difference-charge graph represents the energy stored by a capacitor
- Therefore the work done, or energy stored W in a capacitor is defined by the equation:
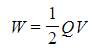
- Where:
- W = energy stored (J)
- Q = charge stored (C)
- V = potential difference across the plates (V)
Worked Example
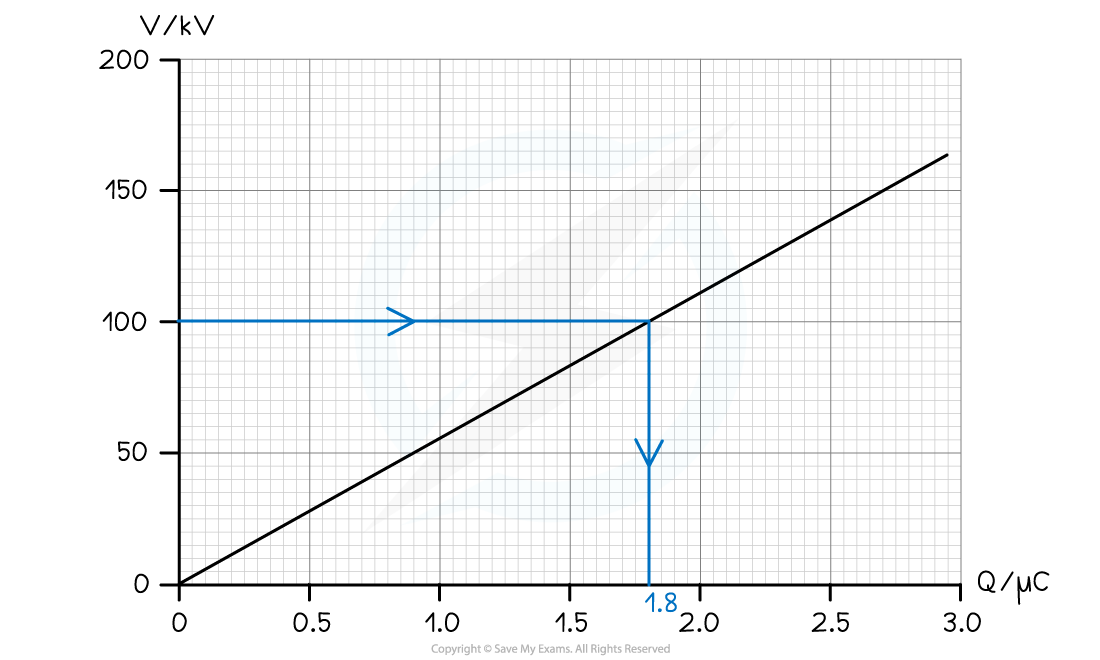
The variation of the potential V of a charged isolated metal sphere with surface charge Q is shown on the graph below.
Using the graph, determine the electric potential energy stored on the sphere when charged to a potential of 100 kV.
Step 1: Determine the charge on the sphere at the potential of 100 kV
-
- From the graph, the charge on the sphere at 100 kV is 1.8 μC
Step 2: Calculate the electric potential energy stored
-
- The electric potential energy stored is the area under the graph at 100 kV
- The area is equal to a right-angled triangle, so, can be calculated with the equation:
-
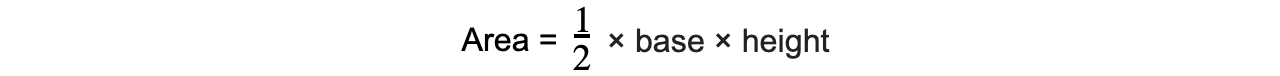
- Substituting in the values gives:
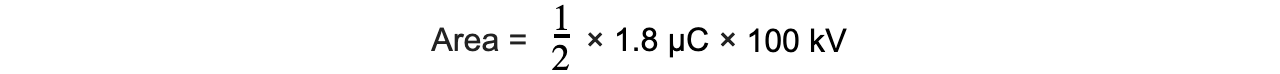
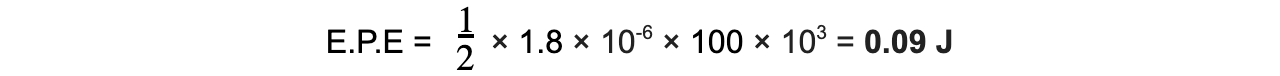
Exam Tip
Remember to always check the units of the charge–potential difference graphs. The charges can often be in µC or the potential difference in kV! The units must be in C and V to get a work done in J.
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
