Edexcel A Level Physics:复习笔记6.3 Applying Conservation of Linear Momentum
Applying Conservation of Linear Momentum
- The principle of conservation of linear momentum states:
The total momentum before a collision = the total momentum after a collision provided no external force acts
- Linear momentum is the momentum of an object that only moves in a straight line
- Momentum is a vector quantity
- This means oppositely-directed vectors can cancel each other out resulting in a net momentum of zero
- If after a collision an object starts to move in the opposite direction to which it was initially travelling, its velocity will now be negative
- Momentum, just like energy, is always conserved
Conservation of Linear Momentum in 1D
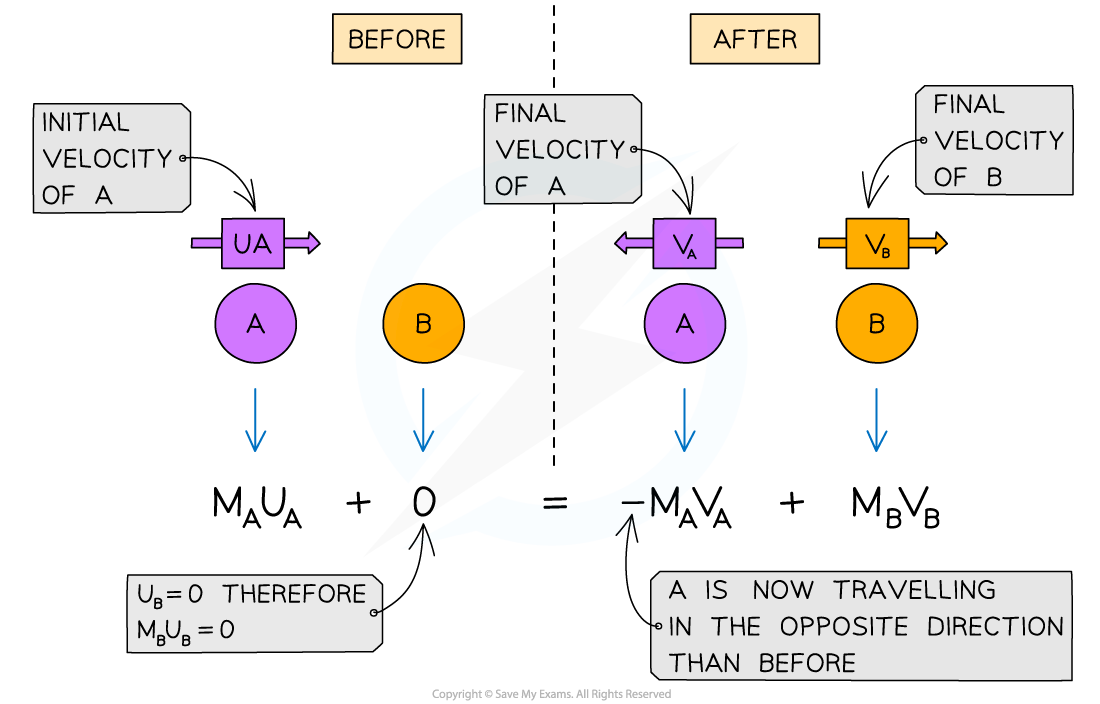
The conservation of momentum in 1D, for two objects A and B colliding then moving apart
Worked Example
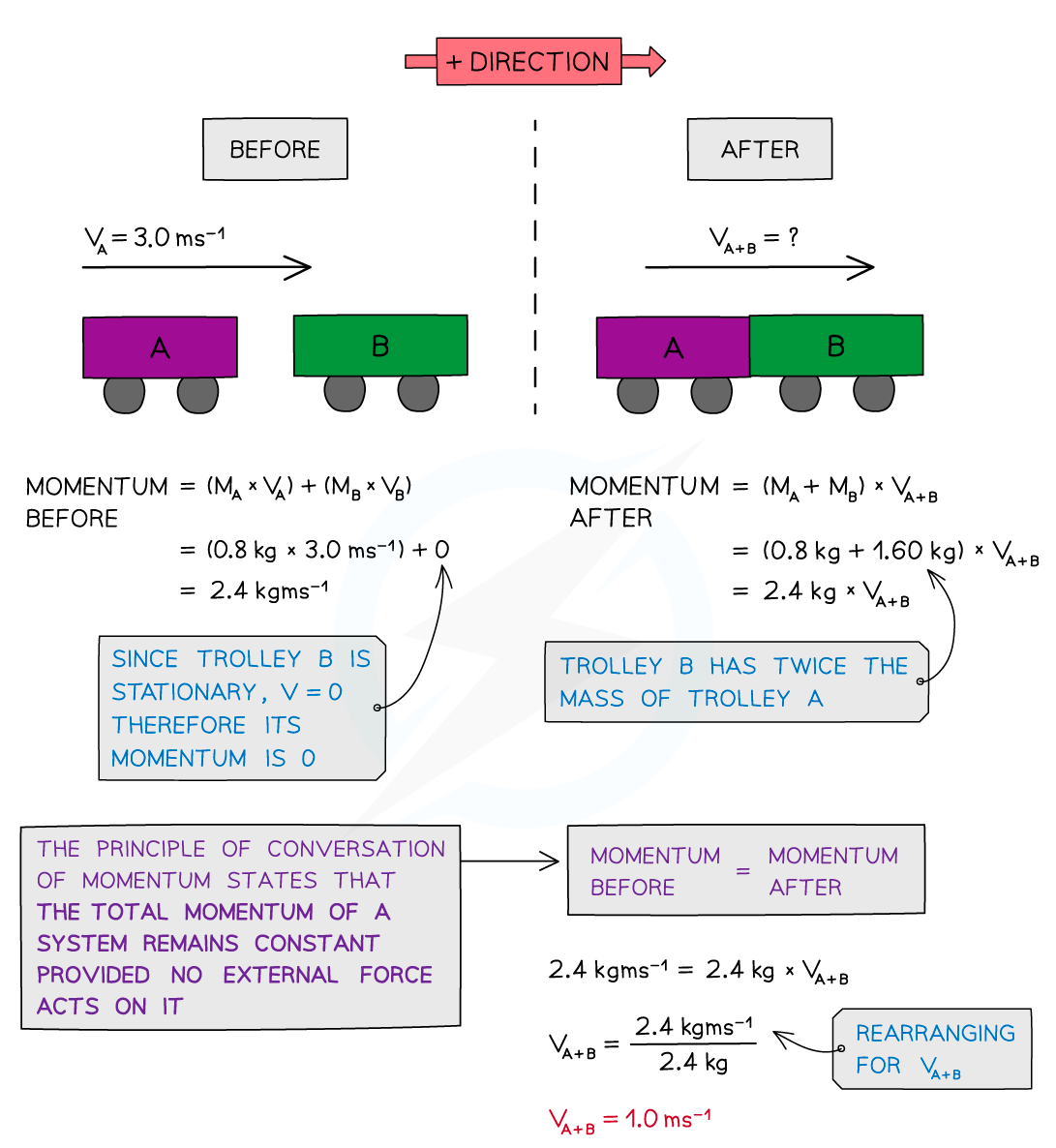
Trolley A of mass 0.80 kg collides head-on with stationary trolley B whilst travelling at
3.0 m s–1. Trolley B has twice the mass of trolley A. On impact, the trolleys stick together.
Using the conversation of momentum, calculate the common velocity of both trolleys after the collision.
Exam Tip
Momentum is a vector quantity, therefore, you should always define a direction to be 'positive' when applying the principle of conservation of momentum. In this worked example, we implicitly took velocity 'to the right' as the positive direction.
Sometimes, however, you might encounter two objects moving towards each other before colliding. If both objects have the same mass m and speed v, then the total momentum (before collision) is zero, because ptotal = (mv) + (–mv) = 0. Note the negative sign indicates a body travelling in the opposite direction.
Conservation of Linear Momentum in 2D
- For objects moving in 2D, there are components of momentum to consider
- This is similar to projectile motion in 2D, in which we consider horizontal and vertical components of motion
Vector R split into its vertical, R cos (30) and horizontal, R sin (30), components
- Each component of momentum is conserved separately
- Since momentum is a vector, it can be resolved into horizontal and vertical components
- The sum of horizontal components will be equal before and after a collision
- The sum of vertical components will be equal before and after a collision
Worked Example
A red snooker ball, travelling at 2.5 m s–1 collides with a green snooker ball, which is at rest. Both snooker balls have the same mass m.
The angle of collision is such that the red ball moves off at 28° below the horizontal at 1.8 m s–1 and the green ball moves off at 55° above the horizontal, with a speed v, as shown.
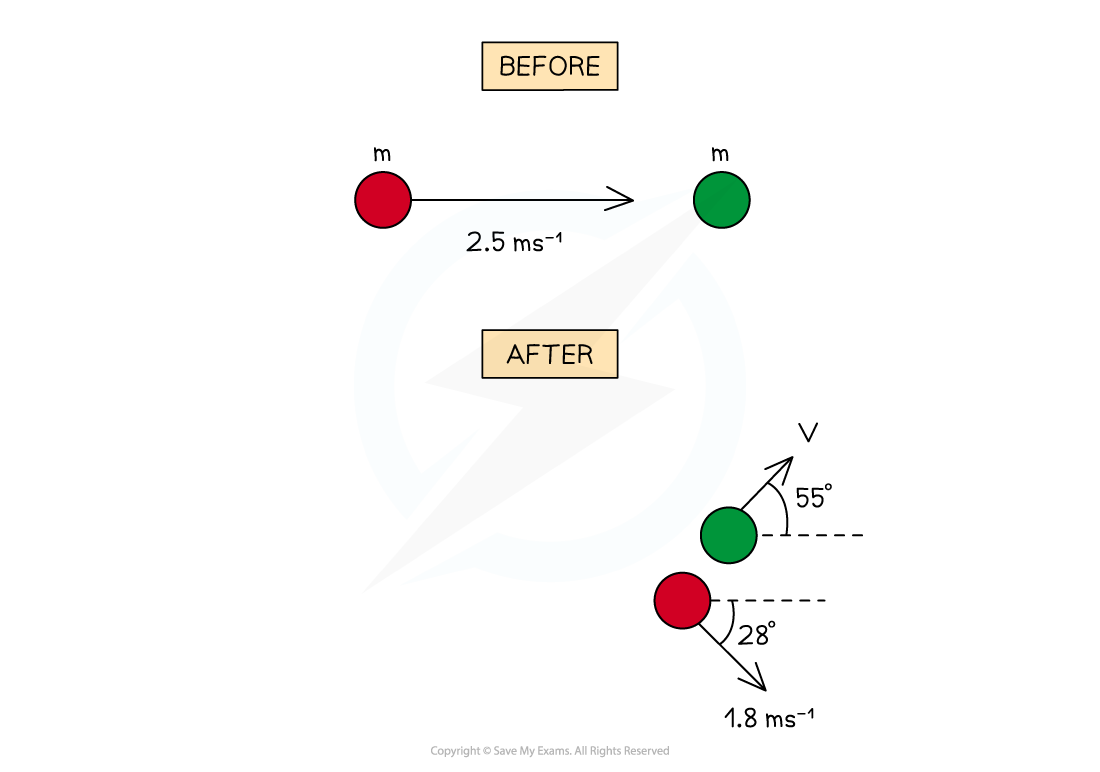
Determine the size of v.
Step 1: Write the conservation of linear momentum for horizontal components
-
- The question is worded in terms of the horizontal direction, so write:
Horizontal momentum before = horizontal momentum after
Step 2: Resolve the velocity of each ball to find the horizontal component:
-
- Since momentum p = mv, then the horizontal component of momentum phoriz = mvhoriz
- Therefore, the horizontal component of the green ball is 1.8 cos 28°
- The horizontal component of the red ball is v cos 55°
Step 3: Substitute quantities into the conservation of momentum
Horizontal momentum before = horizontal momentum after
mured + mugreen = mvhoriz(red) + mvhoriz(green)
m (2.5) + 0 = m (v cos 55°) + m (1.8 cos 28°)
Step 4: Simplify and rearrange to calculate v
2.5 = v cos 55° + 1.8 cos 28°
2.5 = v cos 55° + 1.6
0.9 = v cos 55°
v = 0.9 cos 55° = 1.6 m s–1
Exam Tip
Generally speaking, whenever you see any vector given at an angle to the horizontal or the vertical (e.g. velocity, or momentum), think "resolve"! It's extremely likely you will need to consider the separate components of motion for a projectiles question or for a conservation of momentum question.
Questions which ask you to use the principle of conservation of linear momentum in 2D are usually worth a lot of marks, so make sure you practise lots of questions involving resolving vectors!
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
