Edexcel A Level Physics:复习笔记4.4 Core Practical 4: Investigating Viscosity

Aim of the Experiment

• By allowing small spherical objects of known weight to fall through a fluid until they reach terminal velocity, the viscosity of the fluid can be calculated

Variables

• Independent variable: weight of ball bearing, Ws
• Dependent variable: terminal velocity, vterm
• Control variables:
  • fluid being tested,
  • temperature

Equipment List

• Long measuring cylinder
• Viscous liquid to be tested (thin oil of known density or washing up liquid)
• Stand and clamp
• Metre rule
• Rubber bands
• Steel ball bearings of different weights
• Digital scales
• Vernier calipers
• Digital stopwatch
• Magnet

Method

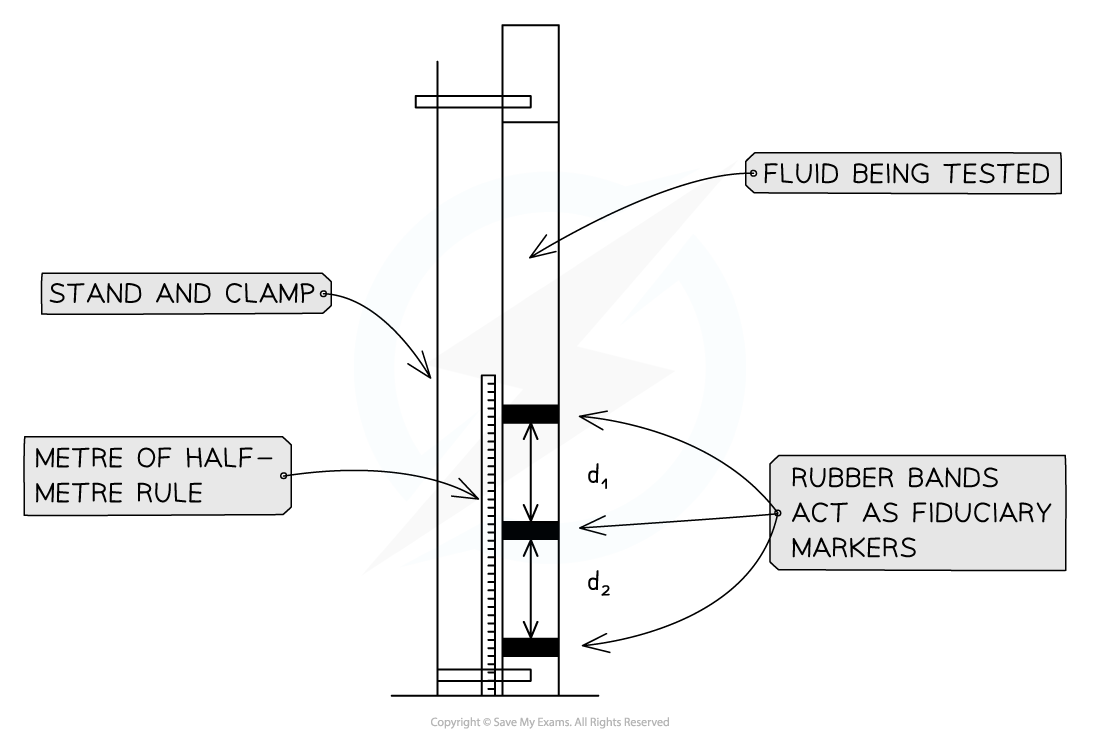
1. Weigh the balls, measure their radius using Vernier callipers and calculate their density
2. Place three rubber bands around the tube. The highest should be far enough below the surface of the liquid to ensure the ball is travelling at terminal velocity when it reaches this band. The remaining two bands should be 10 – 15 cm apart so that time can be measured accurately
3. Release the ball and wait until it reaches the first rubber band. Start the timer at the first band, then use the lap timer to find the time to fall d1 and also d2
   1. If lap timing is not available, two stopwatches operated by different people should be used
   2. If the ball is still accelerating as it passes the markers, they need to be moved downwards until the ball has reached terminal velocity before passing the first mark
4. Measure and record the distances d1 (between the highest and middle rubber band) and d2 between the highest and lowest bands.
5. Repeat at least three times for balls of this diameter and three times for each different diameter
6. Ball bearings are removed from the bottom of the tube using the magnet against the outside wall of the measuring cylinder

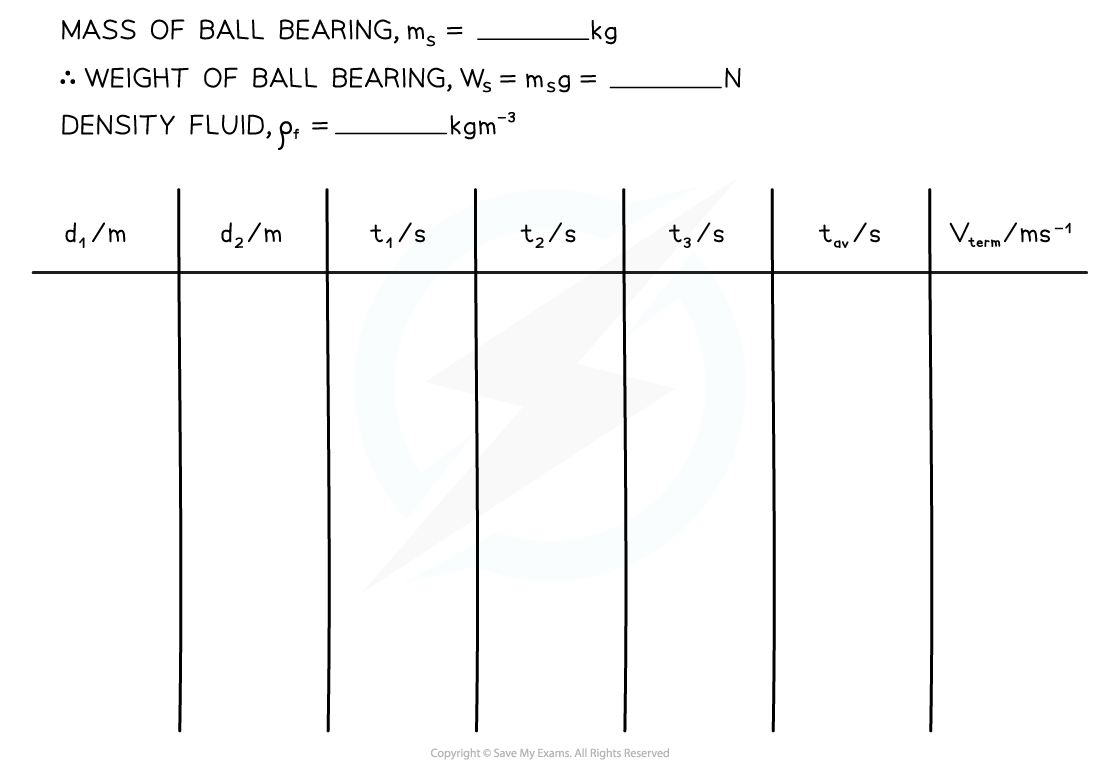
Table of Results:

Analysis

• Terminal velocity is used in this investigation since at terminal velocity the forces in each direction are balanced

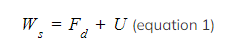(equation 1)

• Where;
  • Ws = weight of the sphere
  • Fd = the drag force (N)
  • U = upthrust (N)

• The weight of the sphere is found using volume, density and gravitational force

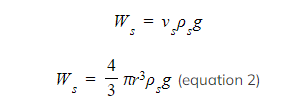
• Where
  • vs = volume of the sphere (m3)
  • ρs = density of the sphere (kg m–3)
  • g = gravitational force (N kg−1)

• Recall Stoke’s Law

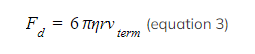
• Upthrust equals the weight of the displaced fluid
  • The volume of displaced fluid is the same as the volume of the sphere
  • The weight of the fluid is found from volume, density and gravitational force as above

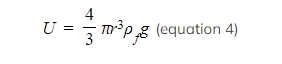
• Substitute equations 2, 3 and 4 into equation 1

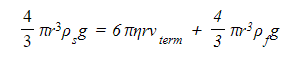
• Rearrange to make viscosity the subject of the equation

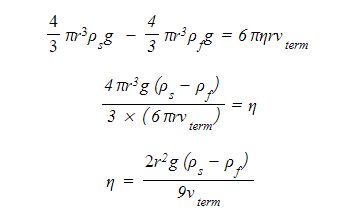
Evaluating the Experiment

Systematic Errors:

• Ruler must be clamped vertically and close to the tube to avoid parallax errors in measurement
• Ball bearing must reach terminal velocity before the first marker

Random errors:

• Cylinder must have a large diameter compared to the ball bearing to avoid the possibility of turbulent flow
• Ball must fall in the centre of the tube to avoid pressure differences caused by being too close to the wall which will affect the velocity

Safety Considerations

• Measuring cylinders are not stable and should be clamped into position at the top and bottom
• Spillages will be slippery and must be cleaned up immediately
• Avoid getting fluids in the eyes