- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Physics:复习笔记2.22 Efficiency
Efficiency
- The efficiency of a system is a measure of how well energy is transferred in a system
- Efficiency is defined as:
The ratio of the useful power or energy transfer output from a system to its total power or energy transfer input
- If a system has high efficiency, this means most of the energy transferred is useful
- If a system has low efficiency, this means most of the energy transferred is wasted
- Determining which type of energy is useful or wasted depends on the system
- When electrical energy is converted to light in a lightbulb, the light energy is useful and the heat energy produced is wasted
- When electrical energy is converted to heat for a heater, the heat energy is useful and the sound energy produced is wasted
- Efficiency can be given as a ratio (between 0 and 1) or a percentage (between 0 and 100%)
- Since efficiency is a ratio, it has no units
- Calculate energy efficiency and power efficiency in the same way, using one of the following equations;

- The energy can be of any form e.g. gravitational potential energy, kinetic energy

- Where power is defined as the energy transferred per unit of time
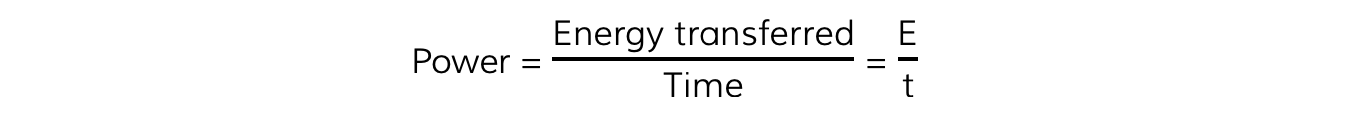
Worked Example
An electric motor has an efficiency of 35 %. It lifts a 7.2 kg load through a height of 5 m in 3 s.
Calculate the power of the motor.
Step 1: Write down the efficiency equation
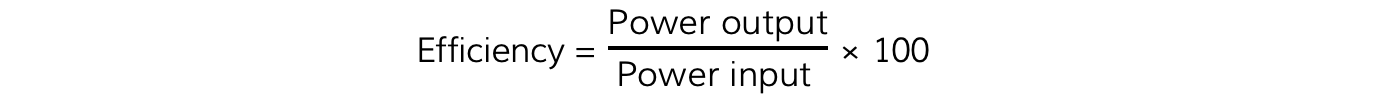
Step 2: Rearrange for the power input 
Step 3: Calculate the power output
-
- The power output is equal to energy ÷ time
- The electric motor transferred electric energy into gravitational potential energy to lift the load
Gravitational potential energy = mgh = 7.2 × 9.81 × 5 = 353.16 J
Power = 353.16 ÷ 3 = 117.72 W
Step 4: Substitute values into power input equation 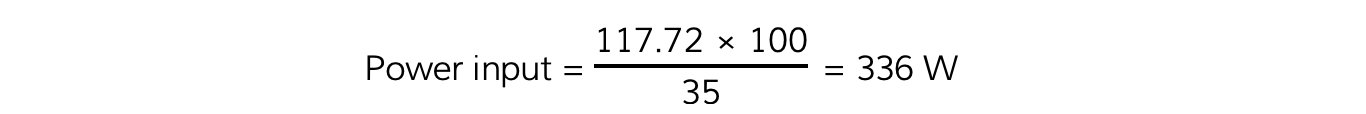
Worked Example
The diagram shows a pump called a hydraulic ram.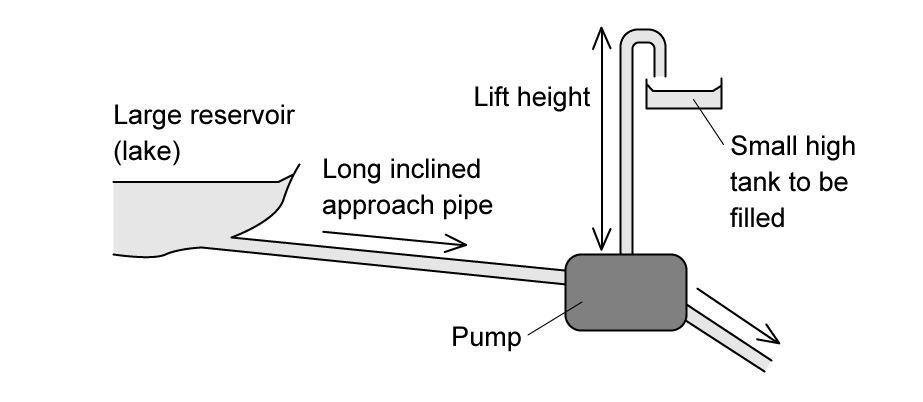
In one such pump, the long approach pipe holds 700 kg of water. A valve shuts when the speed of this water reaches 3.5 m s-1 and the kinetic energy of this water is used to lift a small quantity of water by height of 12m.
The efficiency of the pump is 20%.
Determine the mass of water which could be lifted 12 m
Step 1: Identify the energy conversions and write them in an equation
-
- The kinetic energy of the moving water is converted to gravitational potential energy as it is lifted
- The equation should be that;
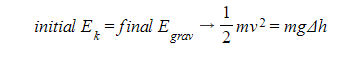
Step 2: Include the efficiency in the equation
-
- Efficiency = 20% meaning 20% of the kinetic energy is converted;
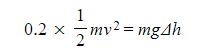
Step 3: Substitute in the values and calculate
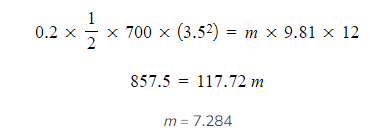
Step 4: Write the answer with the correct significant figures and units
-
- Mass of water lifted, m = 7.3 kg (2 s.f.)
Exam Tip
In efficiency calculations decide before starting where the energy is lost from the system.
In the example above, the pump is what converts the water’s kinetic energy into gravitational potential energy, and it is the pump whose efficiency we are given. That means the losses are from the kinetic energy.
Don't just calculate then deduct the efficiency at the end - this can lead to lots of work for no marks. Which isn't very efficient!
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









