- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
Edexcel A Level Chemistry:复习笔记5.3.2 Born-Haber Cycles
Born-Haber Cycles
- A Born-Haber cycle is a specific application of Hess’ Law for ionic compounds and enable us to calculate lattice enthalpy which cannot be found by experiment
- The basic principle of drawing the cycle is to construct a diagram in which energy increases going up the diagram

The basic principle of a Born-Haber cycle
- The cycle shows all the steps needed to turn atoms into gaseous ions and from gaseous ions into the ionic lattice
- The alternative route to the ionic lattice begins from the enthalpy of formation of the elements in their standard states
Drawing the cycle for sodium chloride
- A good starting point is to draw the elements with their state symbols about a third of the way up the diagram
- This is shown as the left hand side of the equation for the process indicated
- The location is marked by drawing a horizontal bar or line which represents the starting energy level
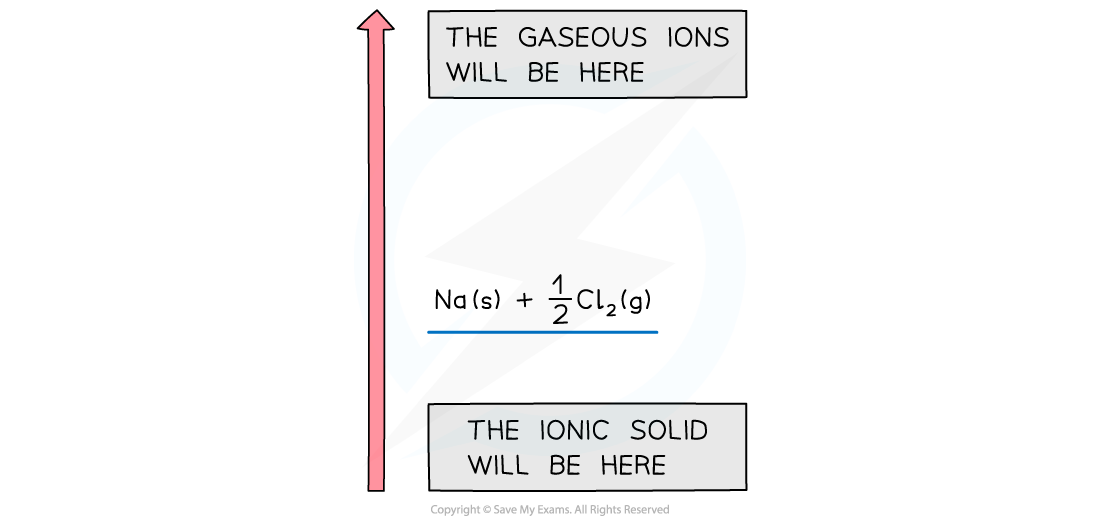
Drawing a Born-Haber cycle step 1
- Next, we need to create the gaseous ions
- This is a two step process of first creating the gaseous atoms and then turning them into ions
- Creating gaseous atoms is a bond breaking process, so arrows must be drawn upwards
- It doesn't matter whether you start with sodium or chlorine
- The enthalpy of atomisation of sodium is
Na (s) → Na (g) ΔHatꝋ = +108 kJ mol -1
- The enthalpy of atomisation of chlorine is
½Cl2 (g) → Cl (g) ΔHatꝋ = +121 kJ mol -1
- We can show the products of the process on the horizontal lines and the energy value against a vertical arrow connecting the energy levels
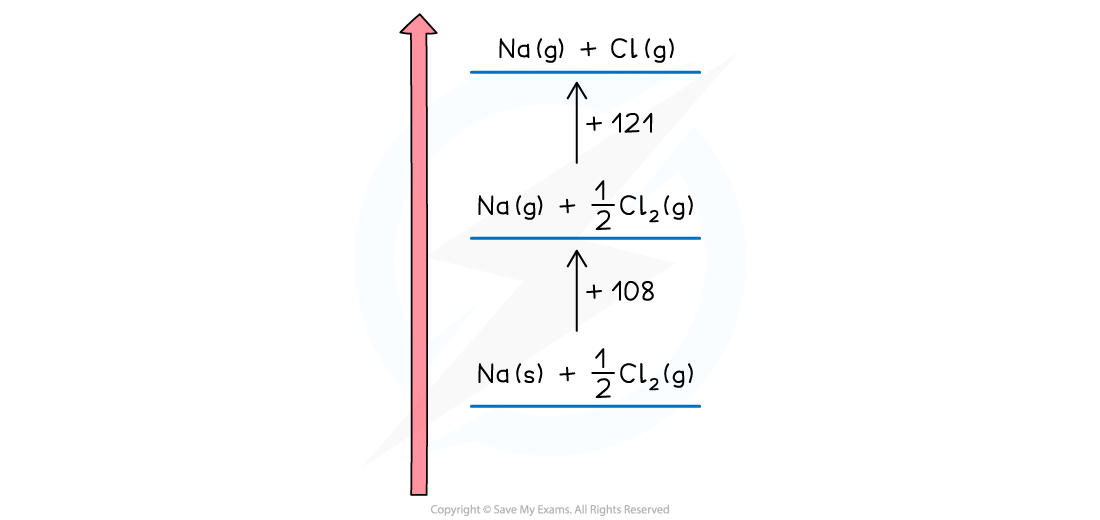
Drawing a Born-Haber cycle step 2 - creating the gaseous atoms
- Now the ions are created
- The sodium ion loses an electron, so this energy change is the first ionisation energy for sodium
Na (g) → Na+ (g) + e– ΔHieꝋ = +500 kJ mol-1
- The change is endothermic so the direction continues upwards
- The chlorine atom gains an electron, so this is electron affinity
Cl (g) + e– → Cl- (g) ΔHeaꝋ = -364 kJ mol-1
- The exothermic change means this is downwards
- The change is displaced to the right to make the diagram easier to read
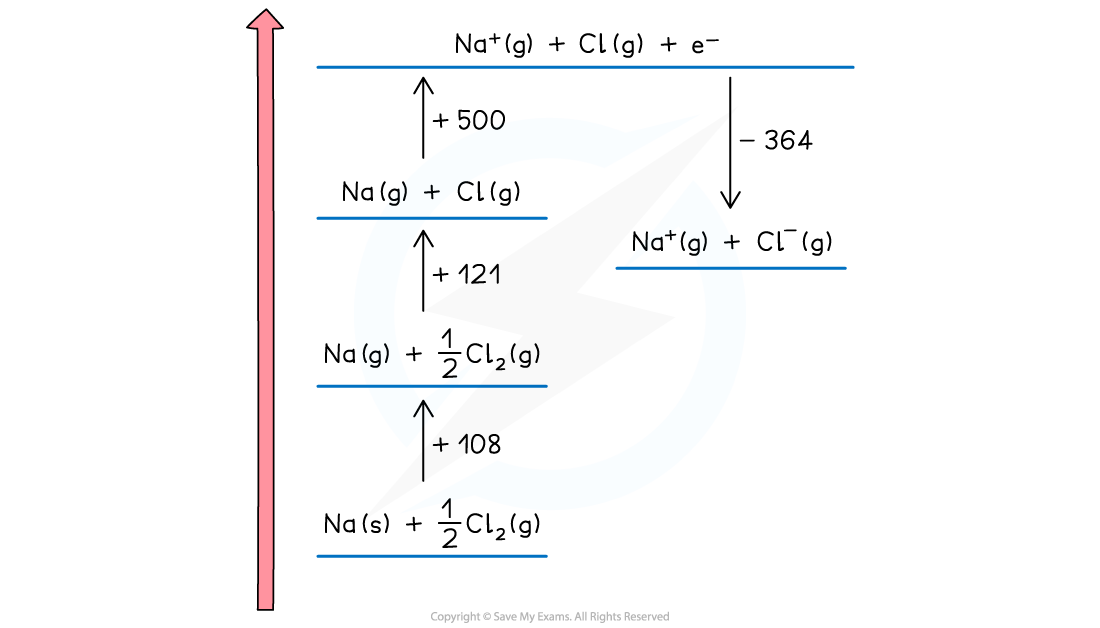
Drawing a Born-Haber cycle step 3 - creating the gaseous ions
- The two remaining parts of the cycle can now be completed
- The enthalpy of formation of sodium chloride is added at the bottom of the diagram
Na (s) + ½Cl2 (g) → NaCl (s) ΔHfꝋ = -411 kJ mol -1
- This is an exothermic change for sodium chloride so the arrow points downwards
- Enthalpy of formation can be exothermic or endothermic, so you may need to show it above the elements ( and displaced to the right) for a endothermic change
- The final change is lattice enthalpy, which is usually shown a formation. For sodium chloride the equation is
Na+(g) + Cl-(g) → NaCl (s) ΔHlattꝋ
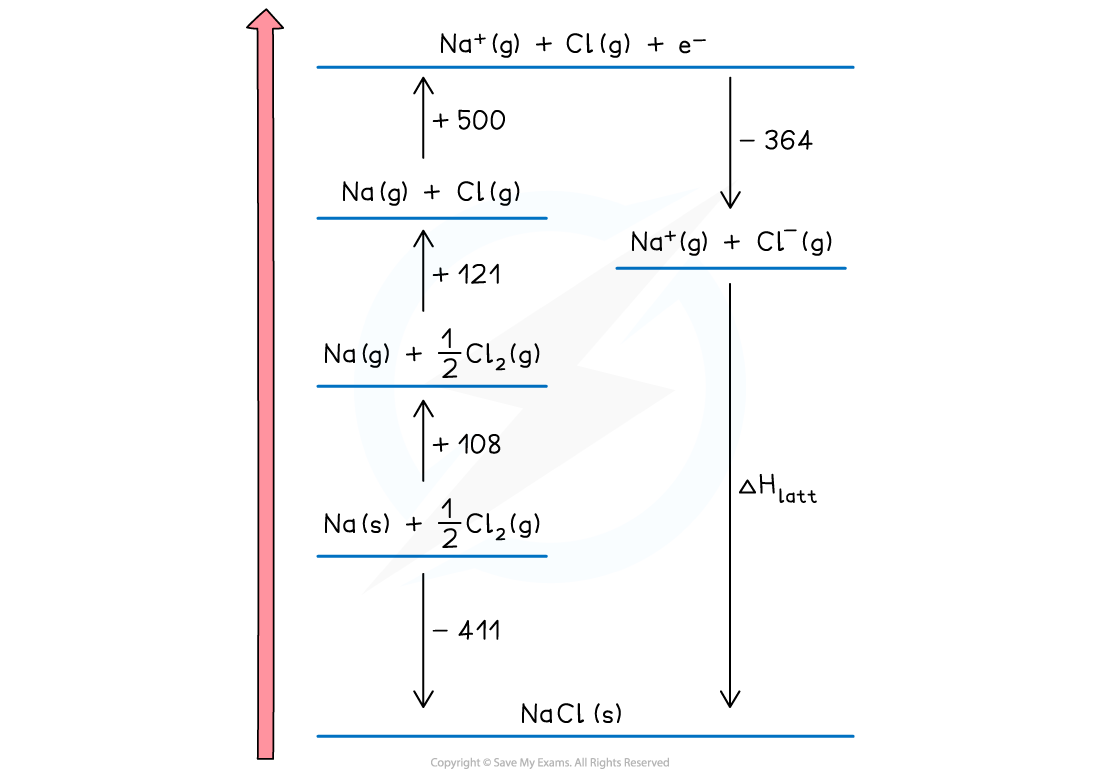
Drawing a Born-Haber cycle step 4 - completing the cycle
- The cycle is now complete
- The cycle is usually used to calculate the lattice enthalpy of an ionic solid, but can be used to find other enthalpy changes if you are given the lattice enthalpy
Worked Example
Constructing a Born-Haber cycle for KCl
Construct a Born-Haber Cycle which can be used to calculate the lattice energy of potassium chloride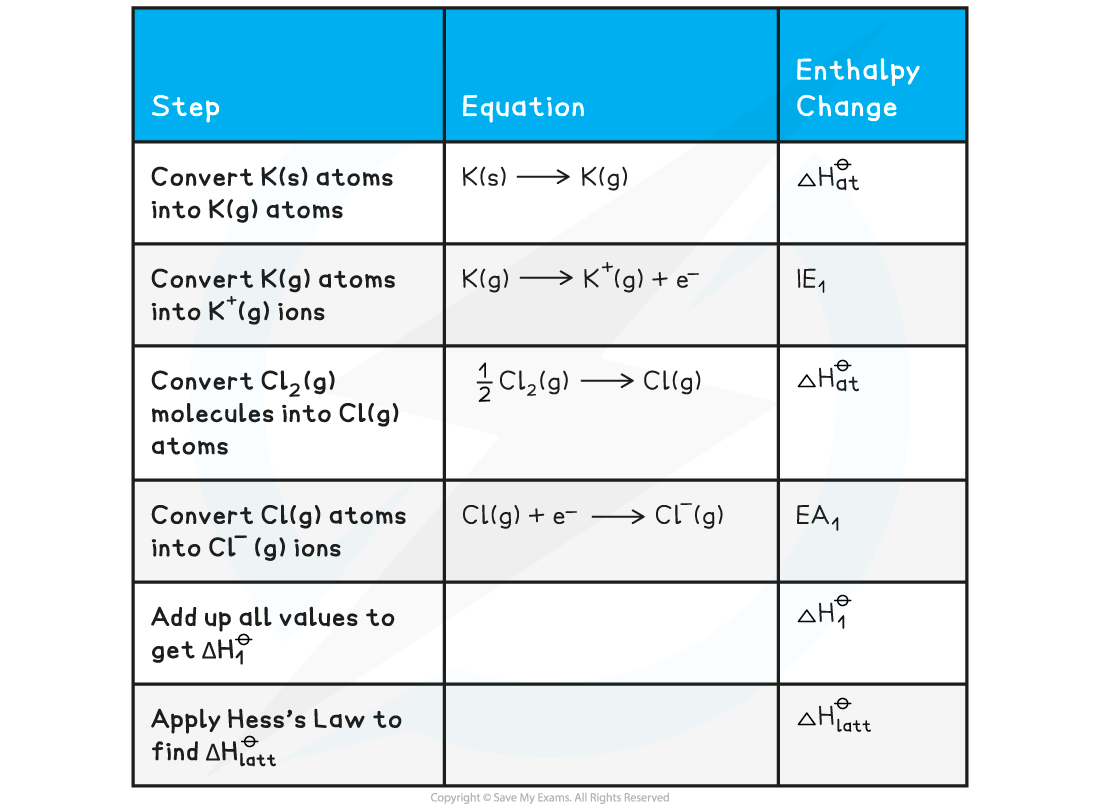
Answer
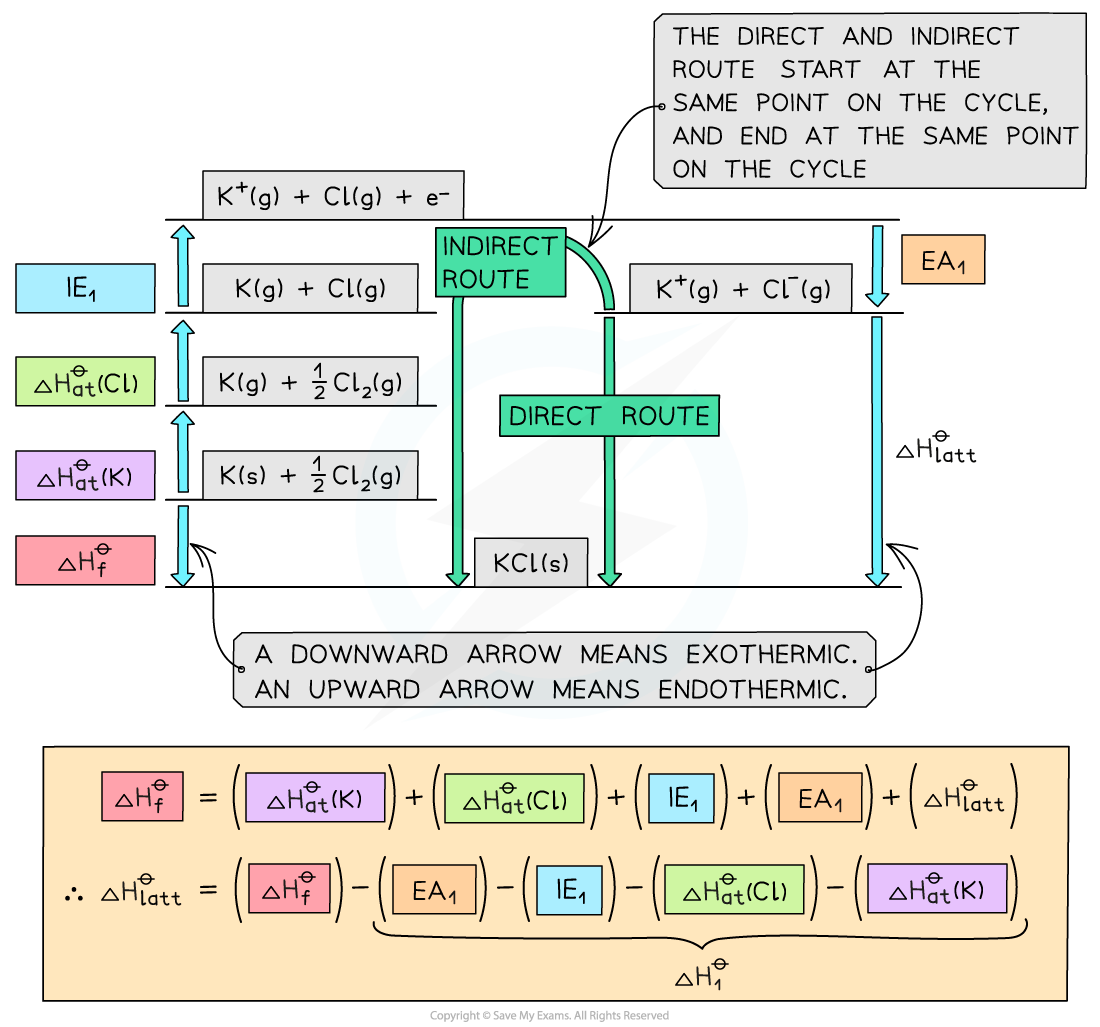
Worked Example
Constructing a Born-Haber cycle for MgO
Construct a Born-Haber Cycle which can be used to calculate the lattice energy of magnesium oxide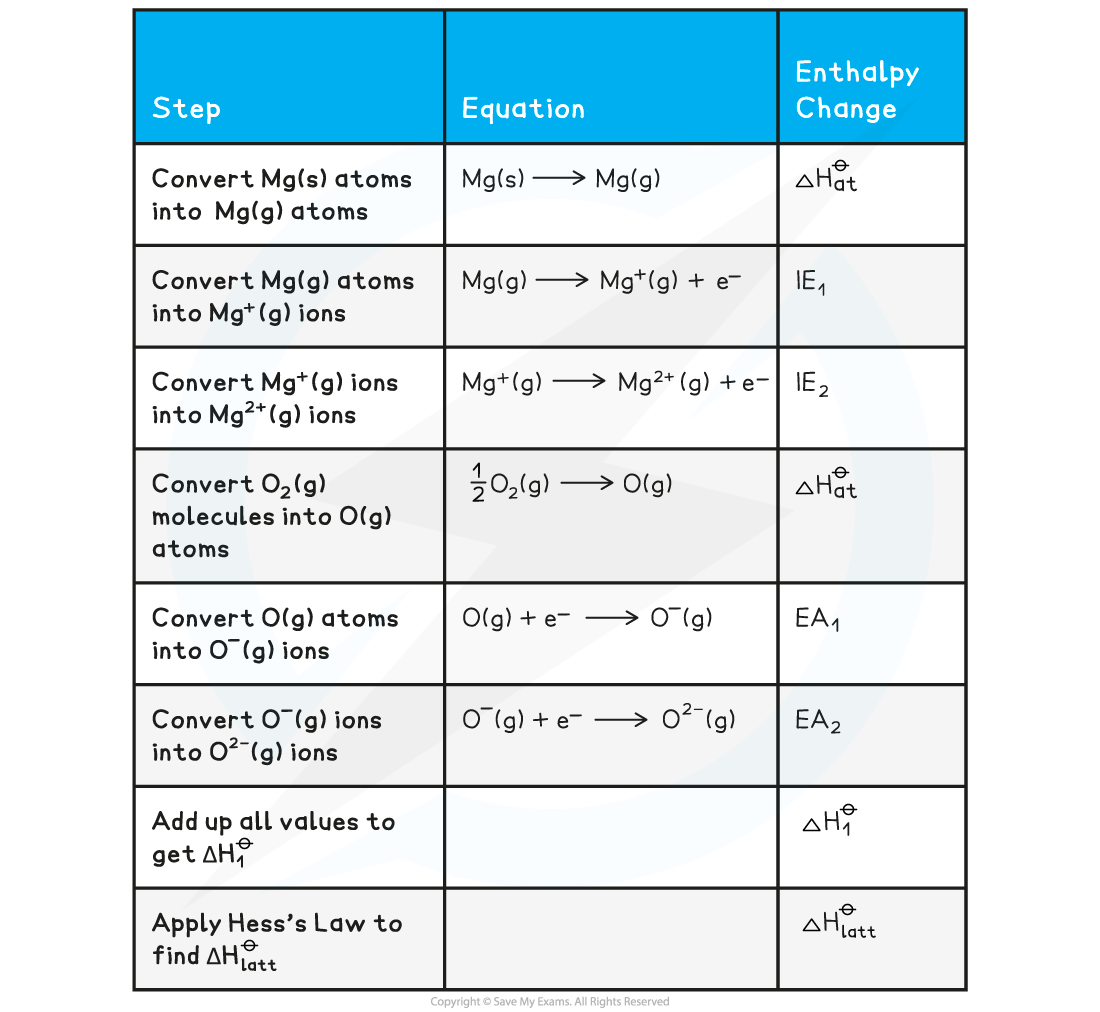
Answer
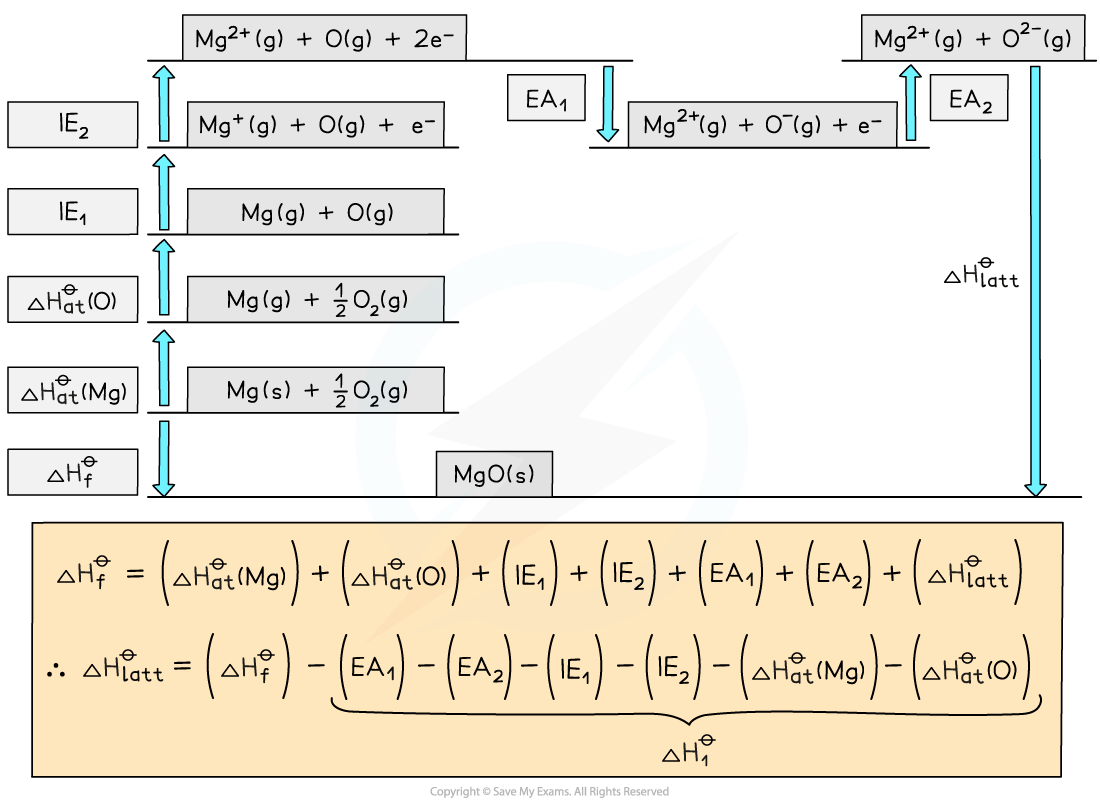
- Once a Born-Haber cycle has been constructed, it is possible to calculate the lattice energy (ΔHlattꝋ) by applying Hess’s law and rearranging:
ΔHfꝋ = ΔHatꝋ + ΔHatꝋ + IE + EA + ΔHlattꝋ
- If we simplify this into three terms, this makes the equation easier to see:
- ΔHlattꝋ
- ΔHfꝋ
- ΔH1ꝋ (the sum of all of the various enthalpy changes necessary to convert the elements in their standard states to gaseous ions)
- The simplified equation becomes
ΔHfꝋ = ΔH1ꝋ + ΔHlattꝋ
So, if we rearrange to calculate the lattice energy, the equation becomes
ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ
- When calculating the ΔHlattꝋ, all other necessary values will be given in the question
- A Born-Haber cycle could be used to calculate any stage in the cycle
- For example, you could be given the lattice energy and asked to calculate the enthalpy change of formation of the ionic compound
- The principle would be exactly the same
- Work out the direct and indirect route of the cycle (the stage that you are being asked to calculate will always be the direct route)
- Write out the equation in terms of enthalpy changes and rearrange if necessary to calculate the required value
- Remember: sometimes a value may need to be doubled or halved, depending on the ionic solid involved
- For example, with MgCl2 the value for the first electron affinity of chlorine would need to be doubled in the calculation, because there are two moles of chlorine atoms
- Therefore, you are adding 2 moles of electrons to 2 moles of chlorine atoms, to form 2 moles of Cl- ions
Worked Example
Calculating the lattice energy of KCl
Given the data below, calculate the ΔHlattꝋ of potassium chloride (KCl) 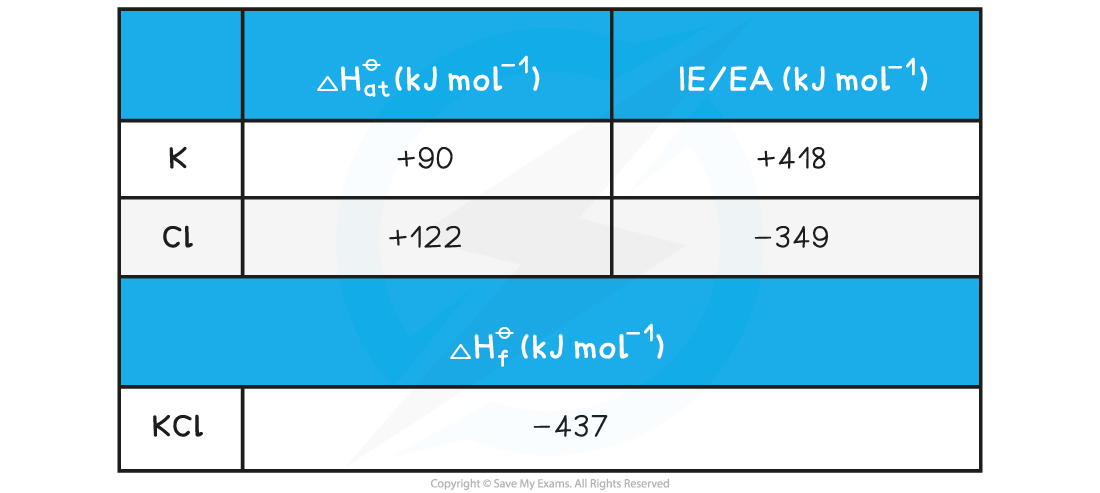
Answer
Step 1: The corresponding Born-Haber cycle is:

Step 2: Applying Hess’ law, the lattice energy of KCl is:
ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ
ΔHlattꝋ = ΔHfꝋ - [(ΔHatꝋ K) + (ΔHatꝋ Cl) + (IE1 K) + (EA1 Cl)]
Step 3: Substitute in the numbers:
ΔHlattꝋ = (-437) - [(+90) + (+122) + (+418) + (-349)] = -718 kJ mol-1
Worked Example
Calculating the lattice energy of MgO
Given the data below, calculate the of ΔHlattꝋ magnesium oxide of magnesium oxide (MgO)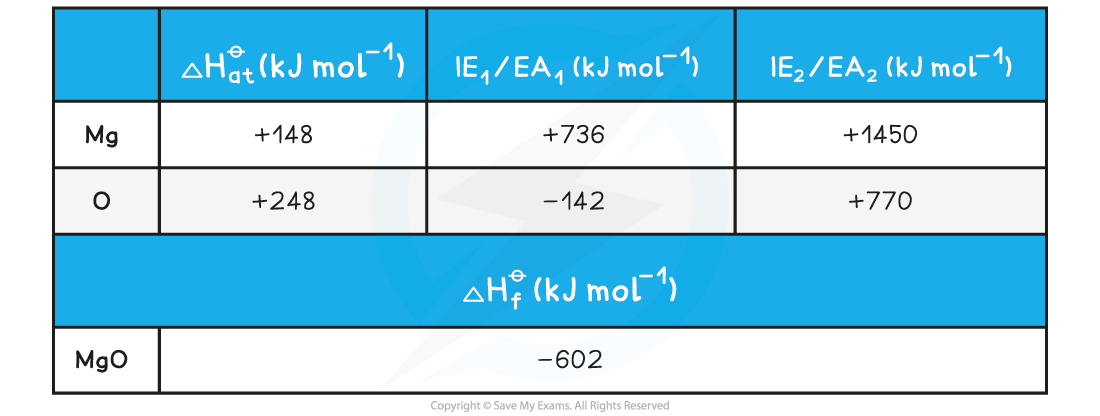
Answer
Step 1: The corresponding Born-Haber cycle is:

Step 2: Applying Hess’ law, the lattice energy of MgO is:
ΔHlattꝋ = ΔHfꝋ - ΔH1ꝋ
ΔHlattꝋ = ΔHfꝋ - [(ΔHatꝋ Mg) + (ΔHatꝋ O) + (IE1 Mg) + (IE2 Mg) + (EA1 O) + (EA2 O)]
Step 3: Substitute in the numbers:
ΔHlattꝋ = (-602) - [(+148) + (+248) + (+736) + (+1450) + (-142) + (+770)]
= -3812 kJ mol-1
转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









