CIE A Level Maths: Pure 3复习笔记8.3.3 Square Roots of a Complex Number - Advanced

Previously we looked at how to find the square roots of a complex number in Cartesian form (a+bi). We can also find square roots using polar  and exponential form ().

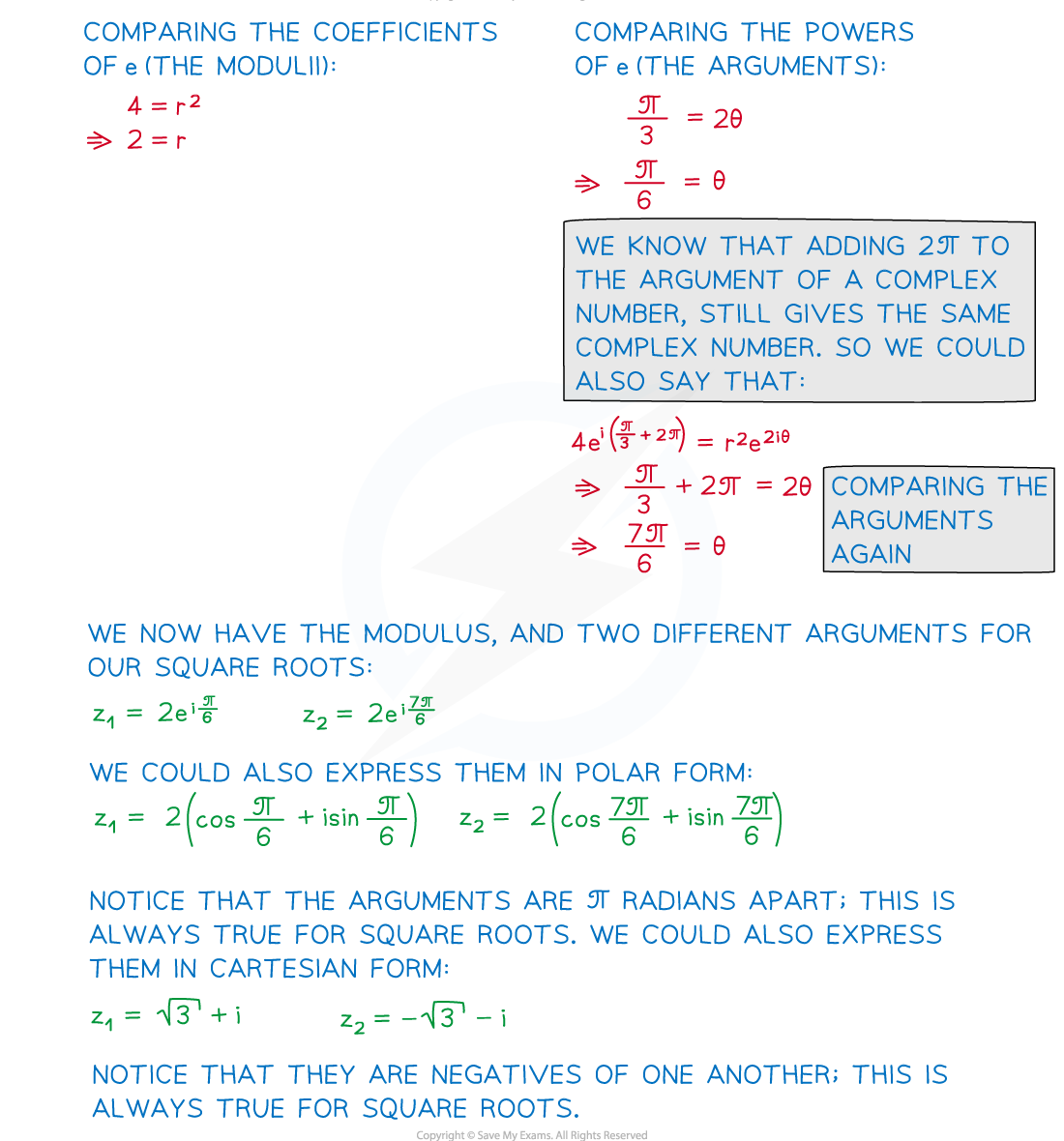
How do I find a square root of a complex number in polar/exponential form?

• Let 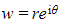be a square root of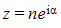
  • 
  • 
• Applying rules of indices:
  • 
• Comparing the coefficients of e (moduli) and powers of e (arguments) we can state:
  • 
    • 
  • 
    • 
• A square root of 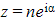 is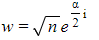
  • • Square root the modulus
    • Halve the argument

How do I find the second square root?

• The second square root is the first one multiplied by -1
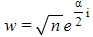  • and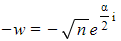
• We can write the second one in polar or exponential form too
• Adding 2π to the argument of a complex number still gives the same complex number
  • So we could also say that
  • Therefore 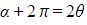 is another possibility
    • 
• So the two square roots of (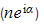) are:
  • 
  • 
• You should notice that the two square roots are π radians apart from each other
  • This is always true when finding square roots
• And if you were to write them in cartesian form they would be negatives of one another
  • E.g. a+bi and -a-bi
  • This is also always true when finding square roots
• This approach can be extended to find higher order roots (e.g. cube roots) by knowing that the nth roots will be radians apart from each other, however this is beyond the specification of this course