- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记8.1.2 Complex Conjugation & Division
Complex Conjugation & Division
When dividing complex numbers, we can use the complex conjugate to make the denominator a real number, which makes carrying out the division much easier.
What is a complex conjugate?
 How do I divide complex numbers?
How do I divide complex numbers?
- When we divide complex numbers, we can express the calculation in the form of a fraction, and then start by multiplying the top and bottom by the conjugate of the denominator:
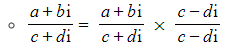 This ensures we are multiplying by 1; so not affecting the overall value
This ensures we are multiplying by 1; so not affecting the overall value- This gives us a real number as the denominator because we have a complex number multiplied by its conjugate (
z z * " alt="z z to the power of asterisk times" data-mathml="<math xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi>z</mi><msup><mi>z</mi><mo>*</mo></msup></mrow><annotation encoding="application/vnd.wiris.mtweb-params+json">{"language":"en","fontFamily":"Times New Roman","fontSize":"18"}</annotation></semantics></math>" />) - This process is very similar to “rationalising the denominator” with surds which you may have studied at GCSE
Worked Example

Exam Tip

转载自savemyexams

最新发布
© 2026. All Rights Reserved. 沪ICP备2023009024号-1









