- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记7.2.1 Vectors in 3 Dimensions
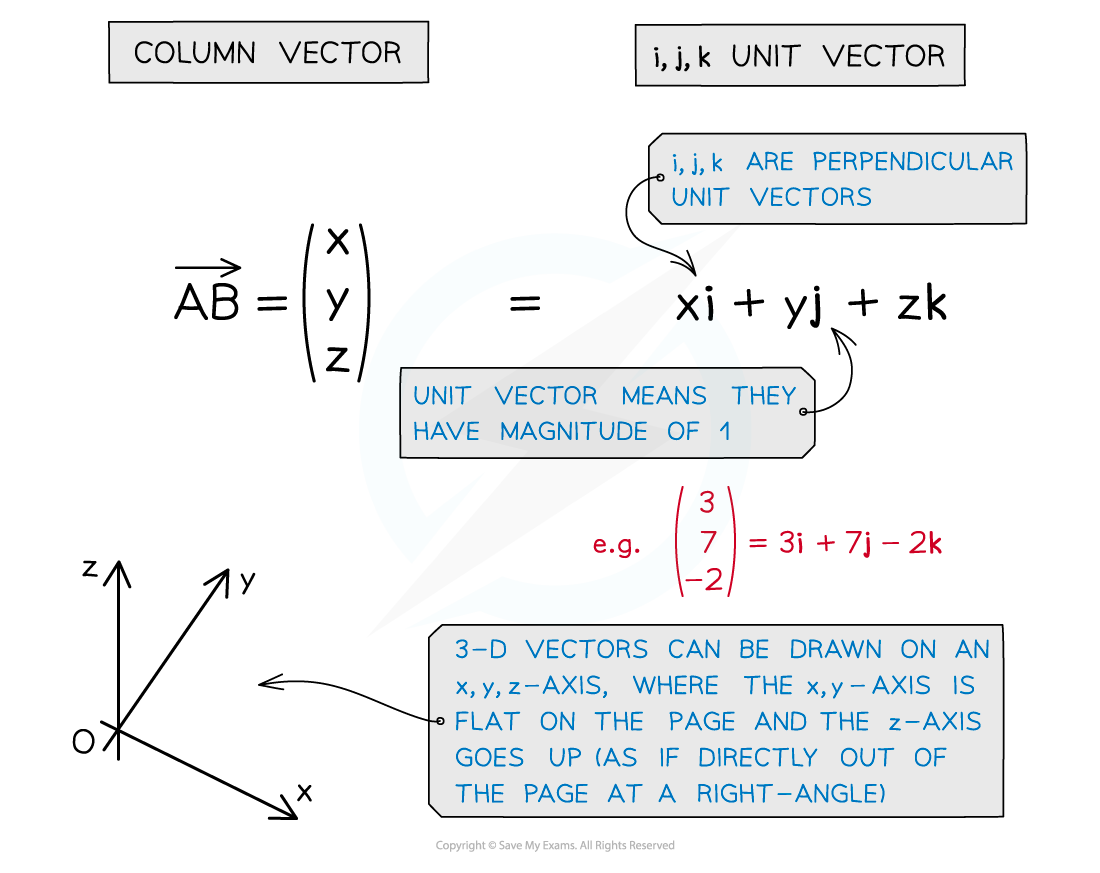
Vectors in 3 Dimensions
What is a 3-D vector?
- Vectors represent a movement of a certain magnitude (size) in a given directionYou should have already come across (2D) vectors at AS (see Basic Vectors)
- 3-D vectors describe the position of a point in a 3-D space in relation to the origin
- They can be represented in different ways such as a column vector or in i, j, k unit vector form
Magnitude of a 3-D vector
- The magnitude of a 3-D vector is simply its size
- Like 2-D vectors we can find the magnitude using Pythagoras’ theorem (see Magnitude Direction)
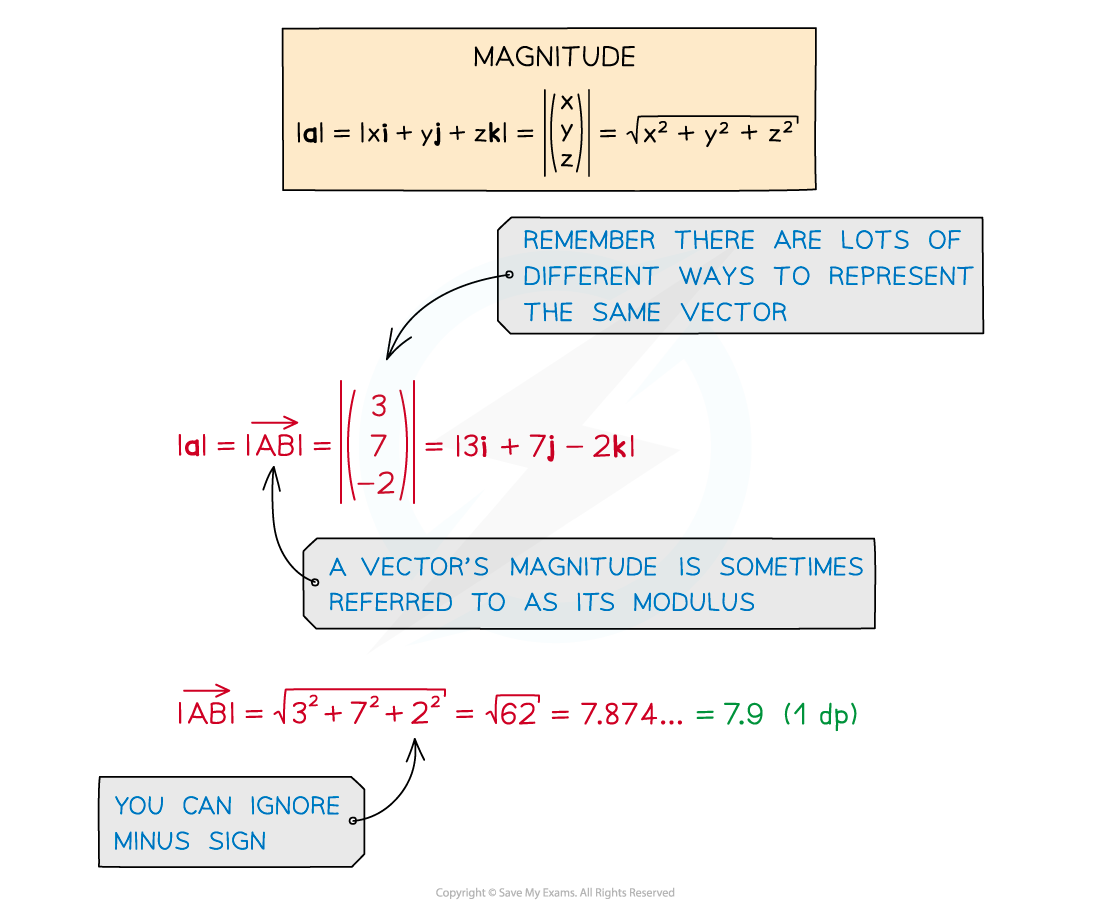
- For 3-D position vectors we can find the distance between two points
- By using the respective co-ordinates we can calculate the magnitude of the vector between them:

3-D vector addition, scalars, parallel vectors and unit vectors
- 3-D vectors work in the same way as 2-D vectors, just in three dimensions rather than two
- Vector addition and subtraction and scalar multiplication can be carried out in exactly the same way, this time involving i, j and k or x, y and z
- 3-D vectors are also parallel if one is a multiple of the other

- Unit vectors in 3-D are found in exactly the same way as in 2-D


Worked Example
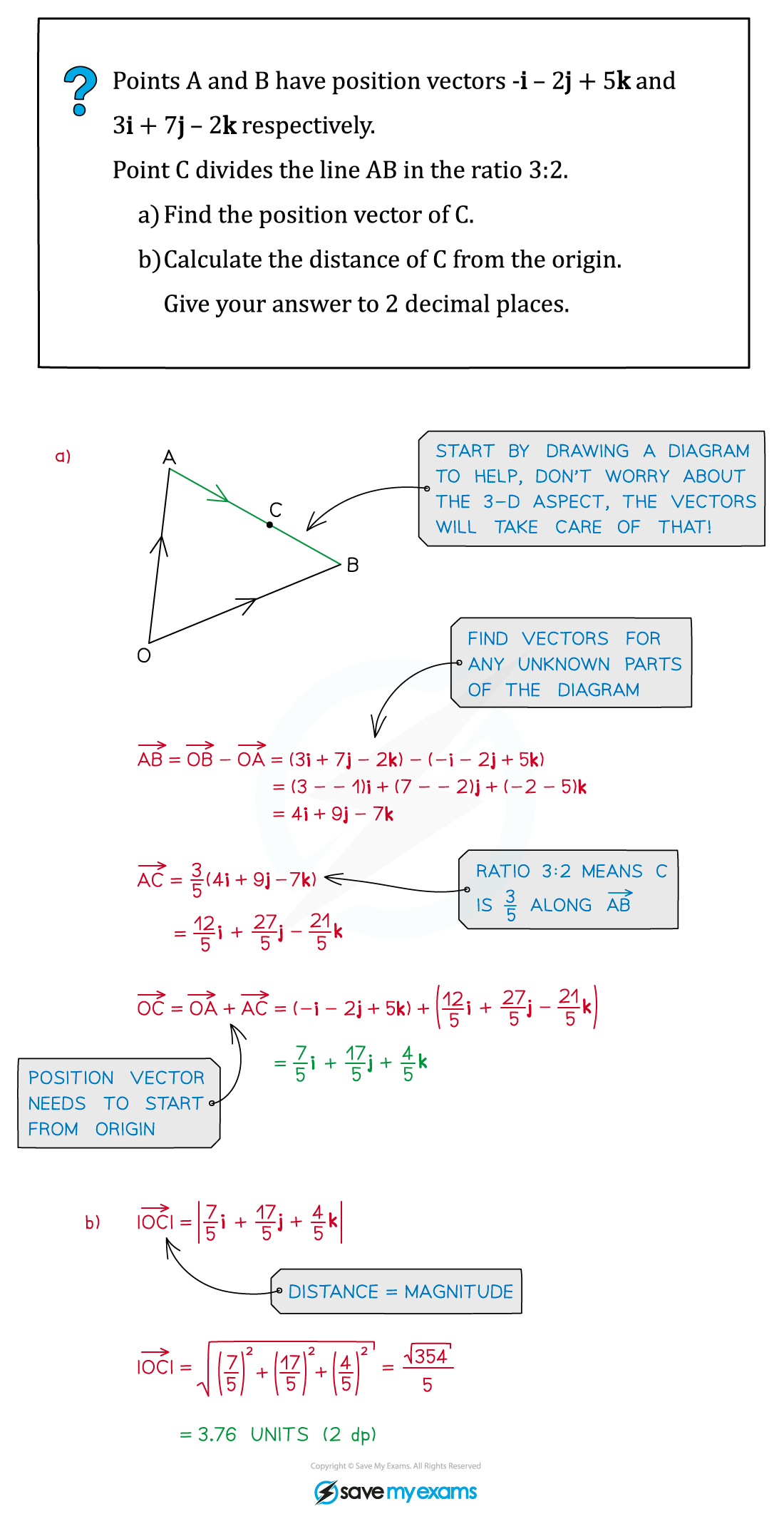
转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









