CIE A Level Maths: Pure 3复习笔记5.1.6 Integration by Parts
Integration by Parts
What is Integration by Parts?
- For integrating the product of two functions - reverse product rule
- Crucially the product is made from u and dv/dx (rather than u and v)
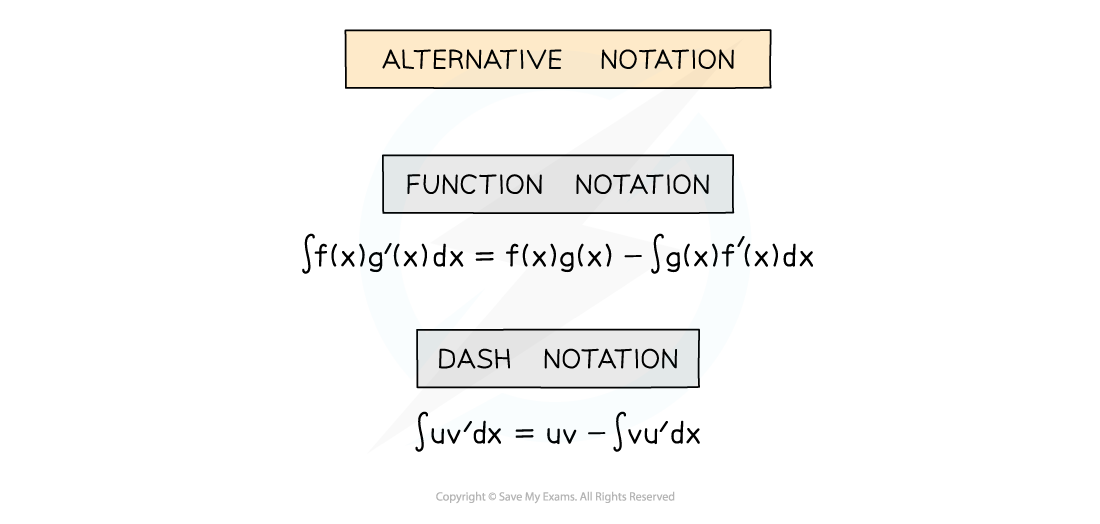
- Alternative notation may be used
How do I use Integration by Parts?
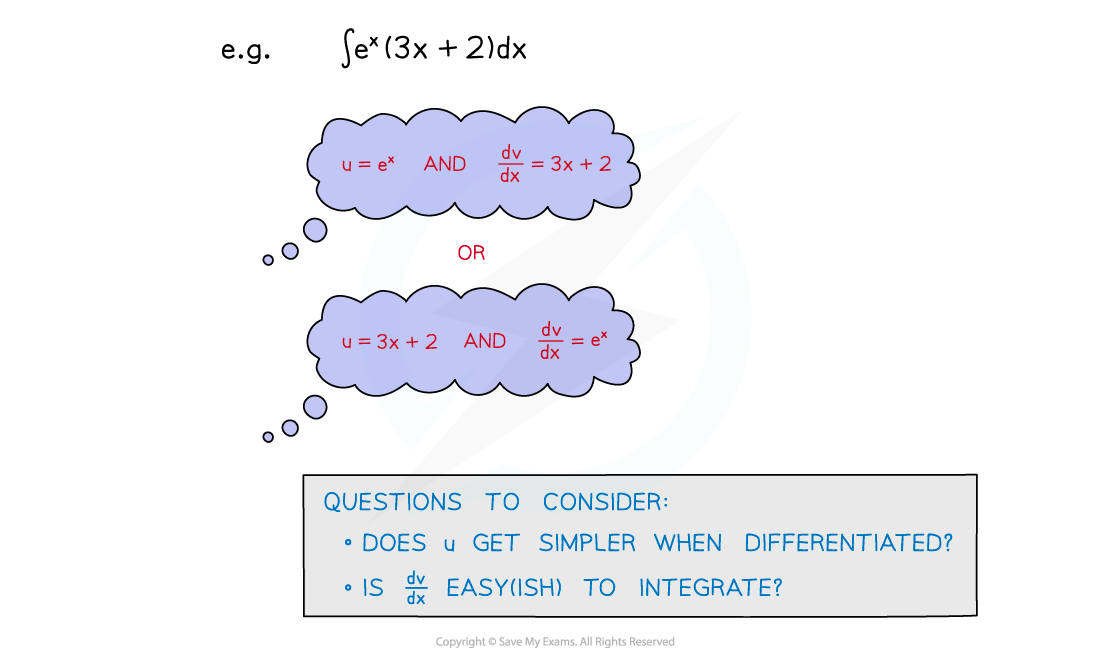
- The hardest part is choosing u and dv/dx as there is no method for doing so
- u, ideally, becomes simpler when differentiated but this is not always possible
- dv/dx should be a function that can be integrated fairly easily
- Be wary of functions that ‘cycle’/’repeat’ when differentiated/integrated
- ex → ex
- sin x → cos x → -sin x → -cos x → sin x
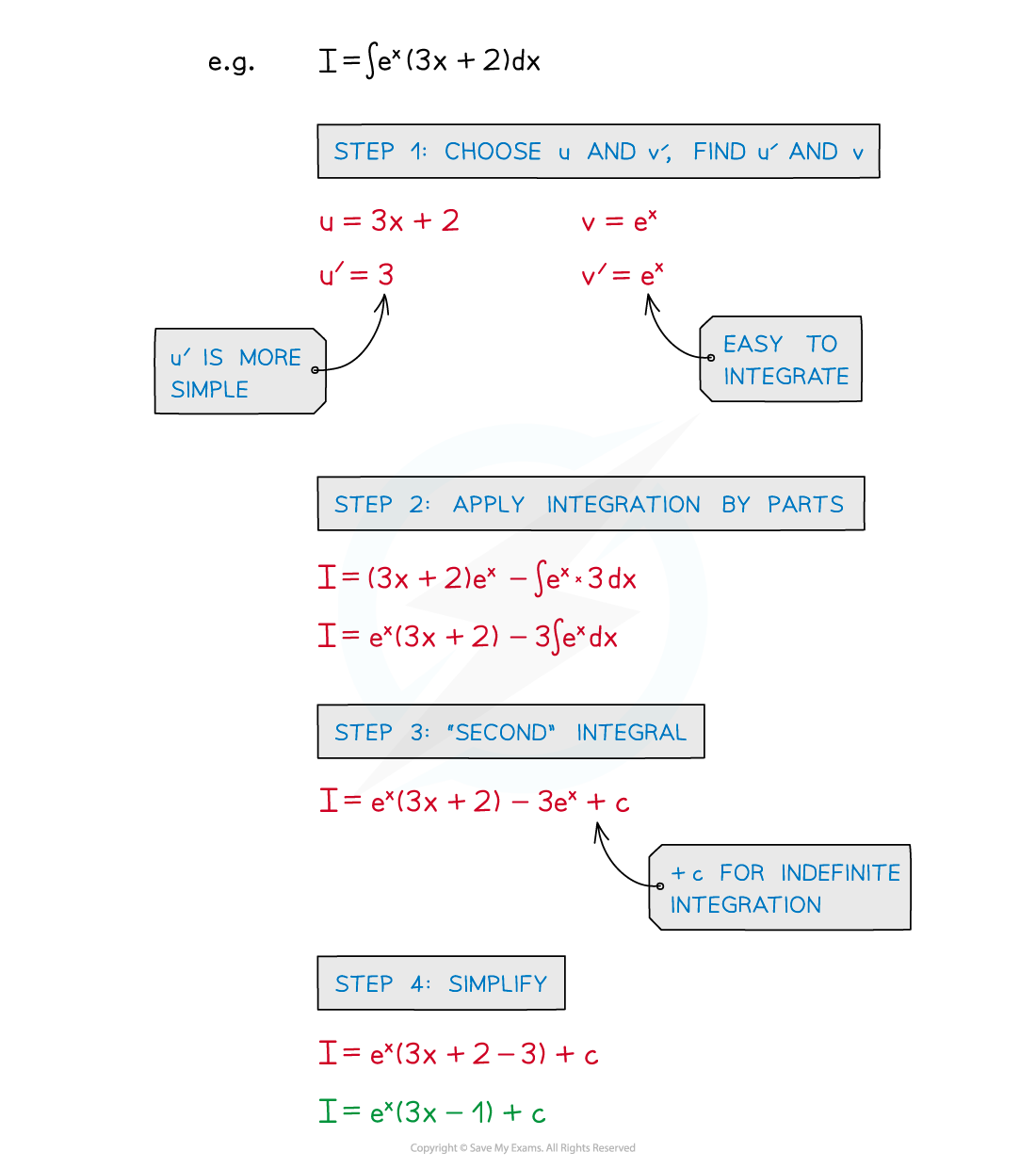
- STEP 1: Choose u and v’, find u’ and v
- STEP 2: Apply Integration by Parts
- Simplify anything straightforward
- STEP 3: Do the ‘second’ integral
- If an indefinite integral remember “+c”, the constant of integration
- STEP 4: Simplify and/or apply limits
What happens if I cannot integrate v × du/dx?
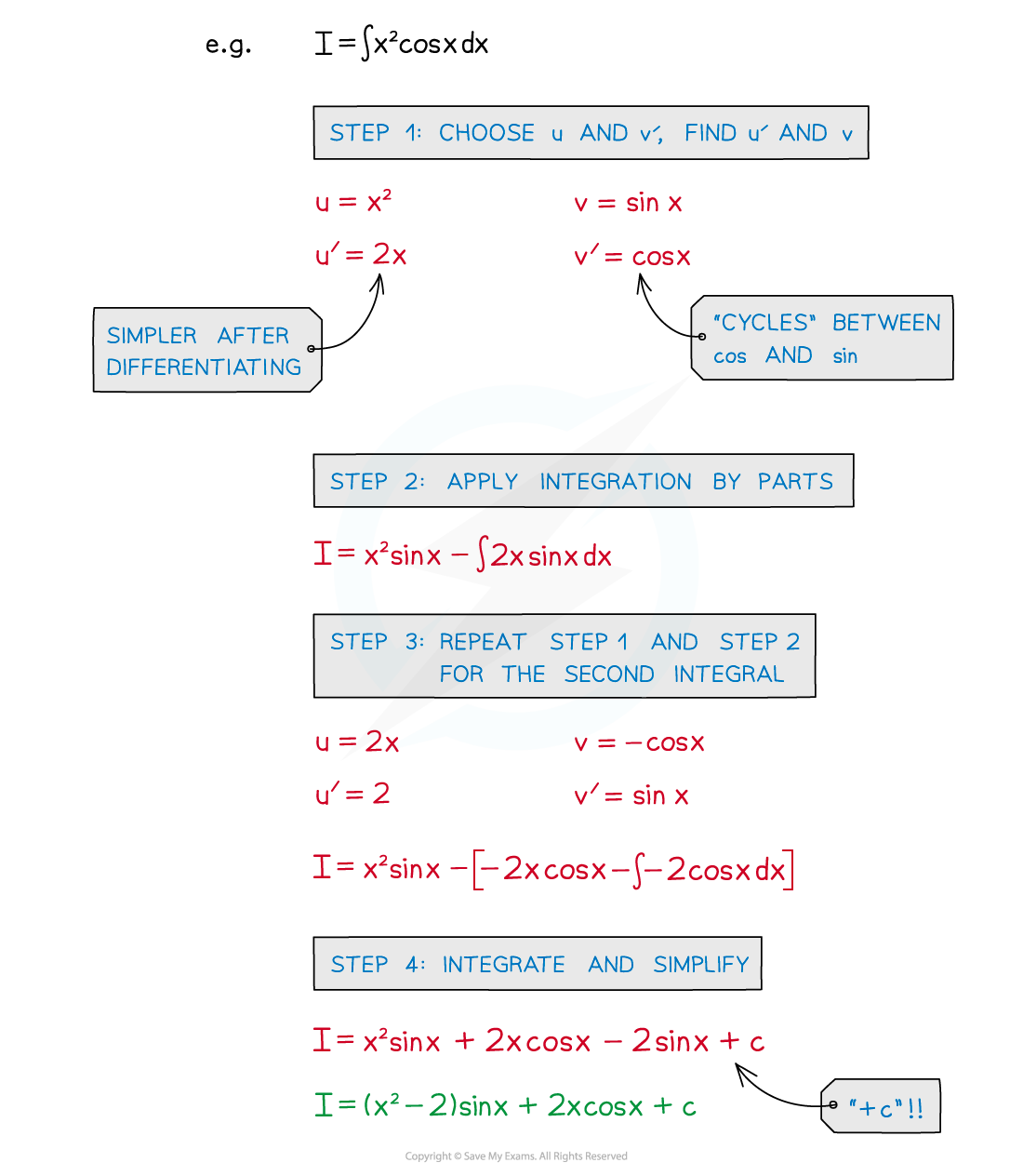
- It is possible integration by parts may need to be applied more than once
ln x
- A classic ‘set piece’ in almost every A level maths textbook ever written!
- In general, rewriting f(x) as 1×f(x) can be a powerful problem-solving technique
- This could be a question in the exam
How do I find a definite integral using parts?
Exam Tip
- Always think about what an elegant, slick, professional maths solution looks like – solutions normally get more complicated at first but quickly get simpler.
- If your work is continuing to get more complicated, stop and check for an error.
- Try to develop a sense of ‘having gone too far down the wrong path’.
- This general advice is useful to remember:
- Is the second integral harder than the first?
- Try swapping your choice of u and dv/dx
- It is rare to have to apply integration by parts more than twice
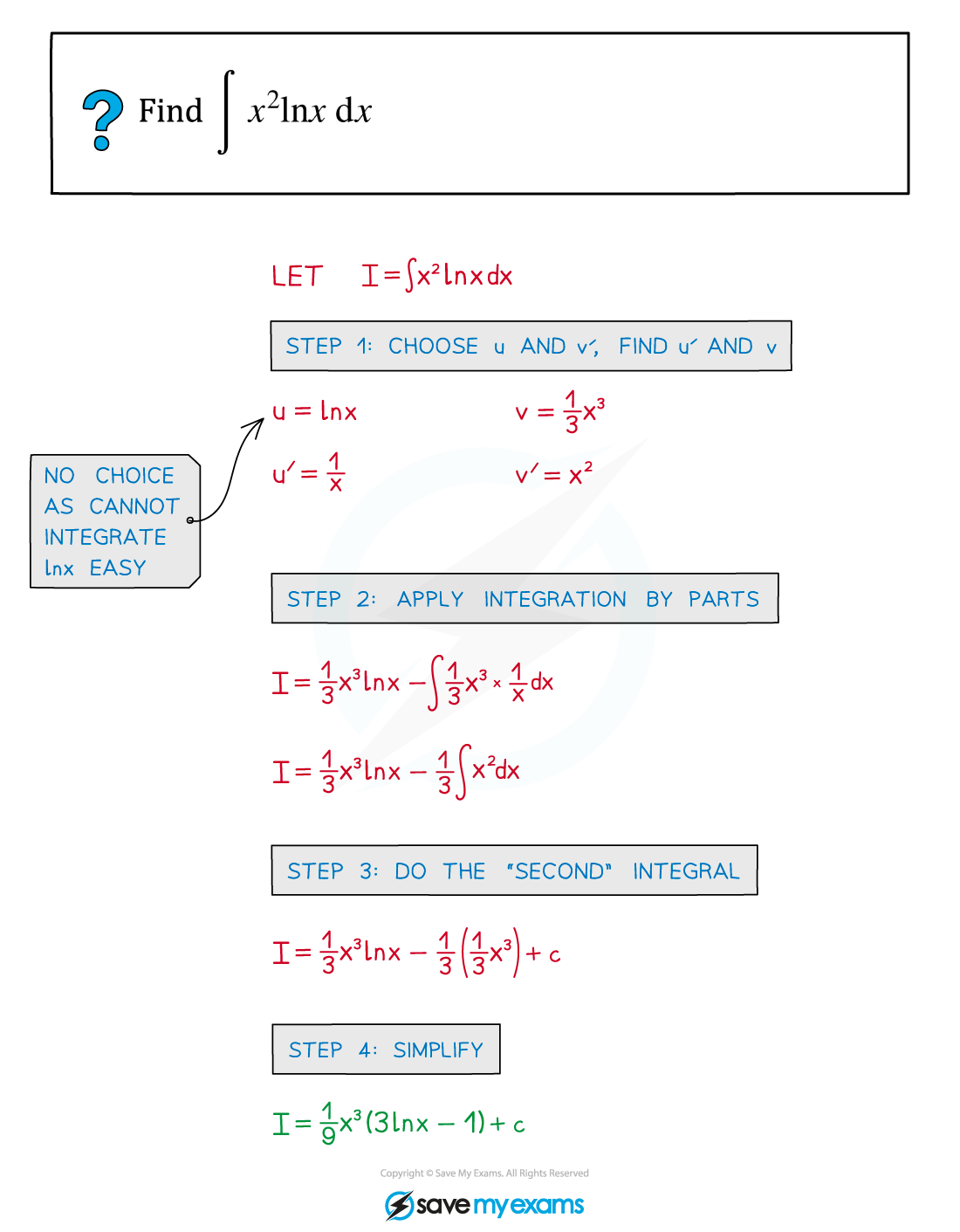
Worked Example
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
2025欧几里得数学竞赛报名开启！
