- 翰林提供学术活动、国际课程、科研项目一站式留学背景提升服务!
- 400 888 0080
CIE A Level Maths: Pure 3复习笔记4.2.1 Implicit Differentiation
Implicit Differentiation
What is implicit differentiation?
- An equation connecting x and y is not always easy to write explicitly in the form y= f(x) or x = f(y)
- However you can still differentiate such an equation implicitly using the chain rule:


- Combining this with the product rule gives us:
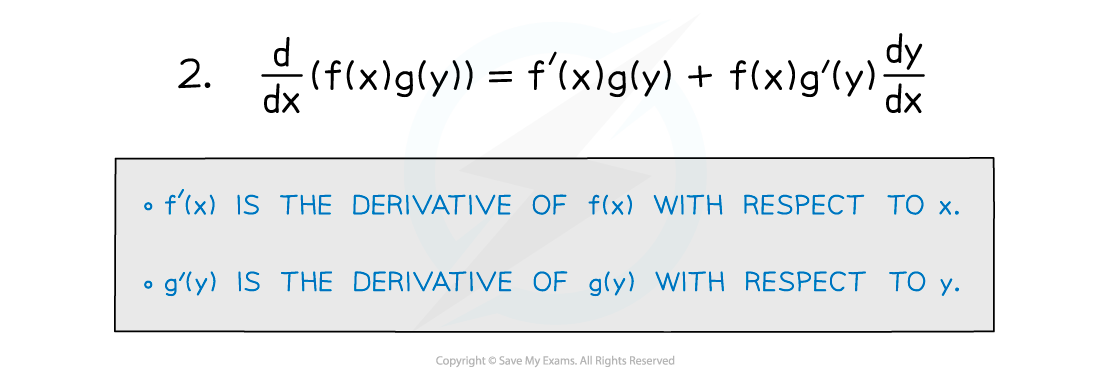
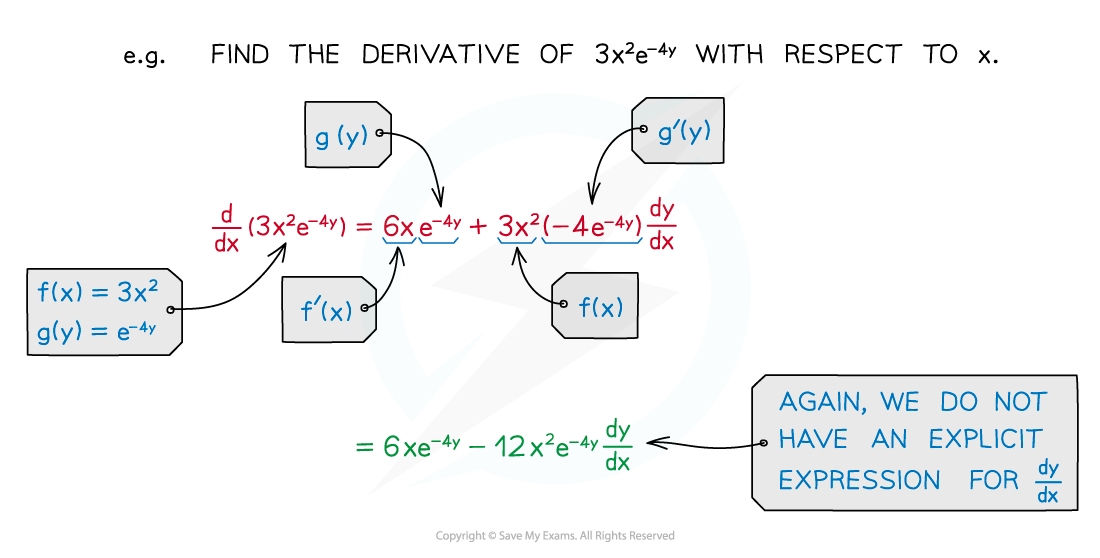
- These two special cases are especially useful:
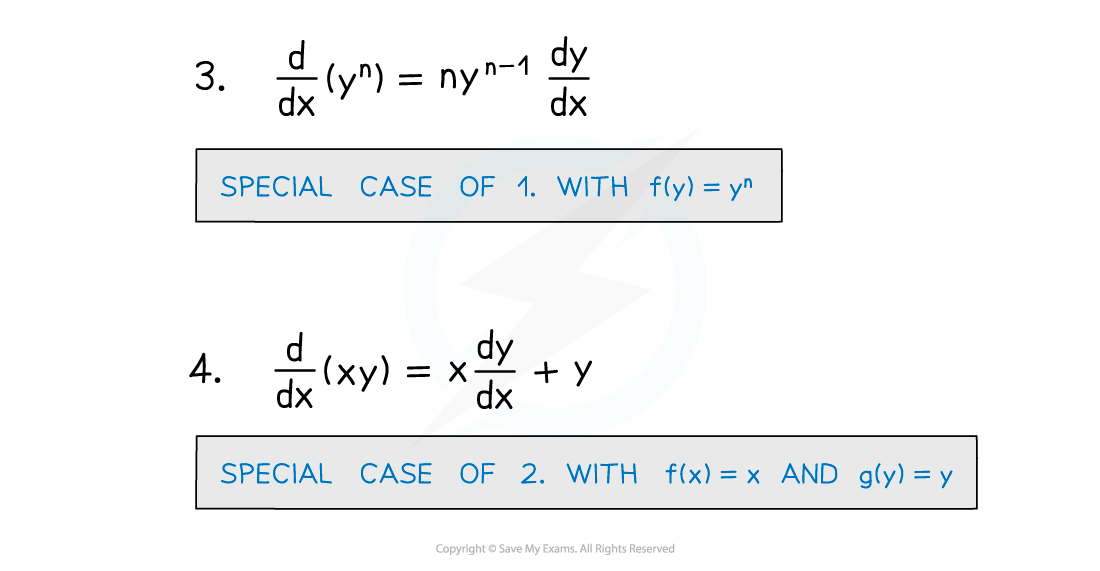
- When x and y are connected in an equation you can differentiate both sides with respect to x and rearrange to find a formula (usually in terms of x and y ) for dy/dx
- Note that dy/dx is a single algebraic object
- When rearranging do not treat dy/dx as a fraction
- Especially do not try to separate dy and dx and treat them as algebraic objects on their own!
Exam Tip
- When using implicit differentiation you will not always be able to write dy/dx simply as a function of x.
- However, this does not stop you from answering questions involving the derivative.
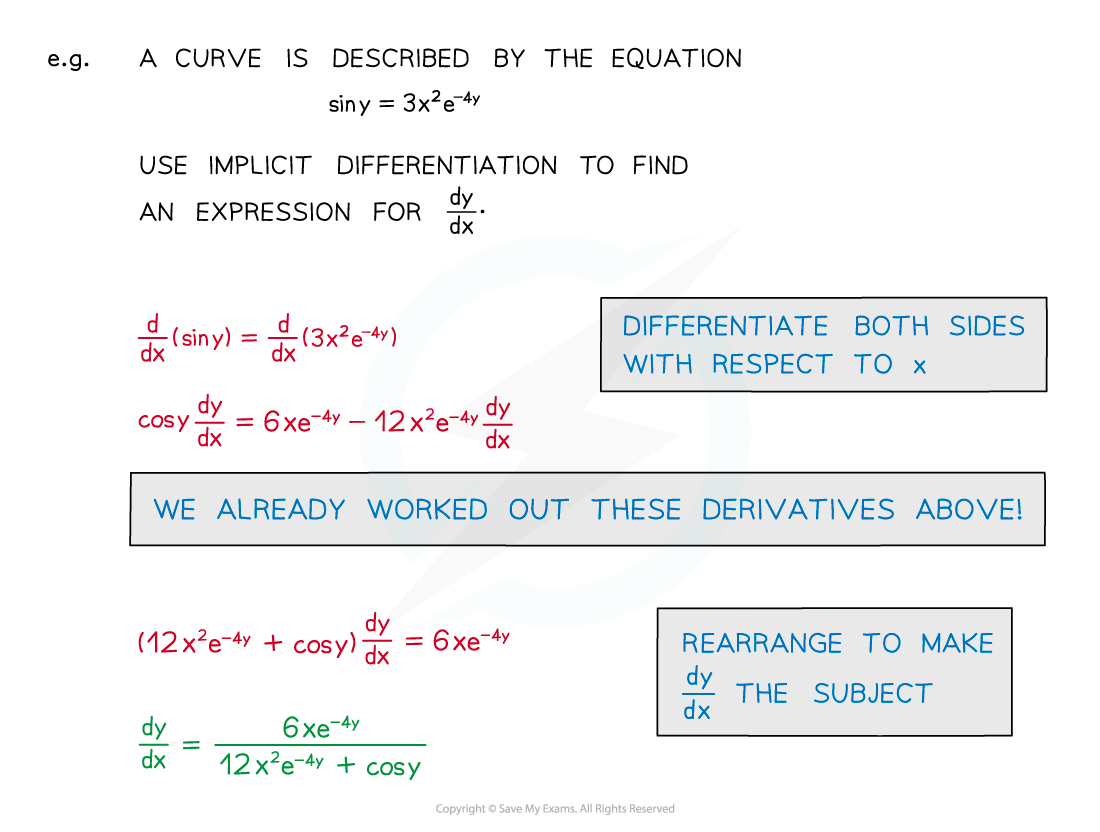
Worked Example

转载自savemyexams

最新发布
© 2025. All Rights Reserved. 沪ICP备2023009024号-1









