CIE A Level Maths: Pure 1复习笔记6.2.4 Volumes of Revolution

What is a volume of revolution around the x-axis?

• A volume of revolution is the volume of this solid formed

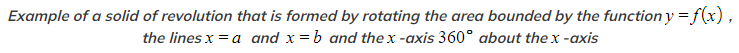How do I find the volume of revolution around the x-axis?

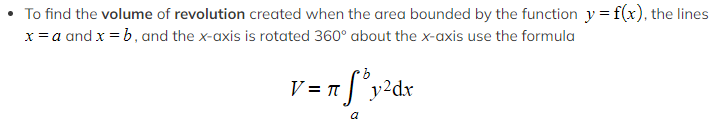• The formula may look complicated or confusing at first due to the y and dx
  • remember that y is a function of x
  • once the expression for y is substituted in, everything will be in terms of x
• π is a constant so you may see this written either inside or outside the integral
• This is not given in the formulae booklet
  • The formulae booklet does list the volume formulae for some common 3D solids – it may be possible to use these depending on what information about the solid is available

How do I solve problems involving volumes of revolution around the x-axis?

• Visualising the solid created is helpful
  • Try sketching some functions and their solids of revolution to help
•  STEP 1 Square y
  • Do this first without worrying about π or the integration and limits
• STEP 2 Identify the limits a and b (which could come from a graph)
• STEP 3 Use the formula by evaluating the integral and multiplying by π
  • The answer may be required in exact form (leave in terms of π)
    • If not, round to three significant figures (unless told otherwise)
• Trickier questions may give you the volume and ask for the value of an unknown constant elsewhere in the problem

What is a volume of revolution around the y-axis?

• A volume of revolution is the volume of this solid formed

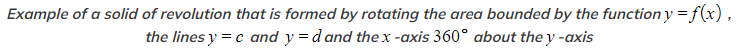How do I find the volume of revolution around the y-axis?

How do I solve problems involving volumes of revolution around the y-axis?