CIE A Level Maths: Pure 1复习笔记1.2.5 Quadratic Inequalities
Quadratic Inequalities
Quadratic inequalities
- Similar to quadratic equations
- Sketching a quadratic graph is essential
- Can involve the discriminant or applications in mechanics and statistics
How do I solve quadratic inequalities?
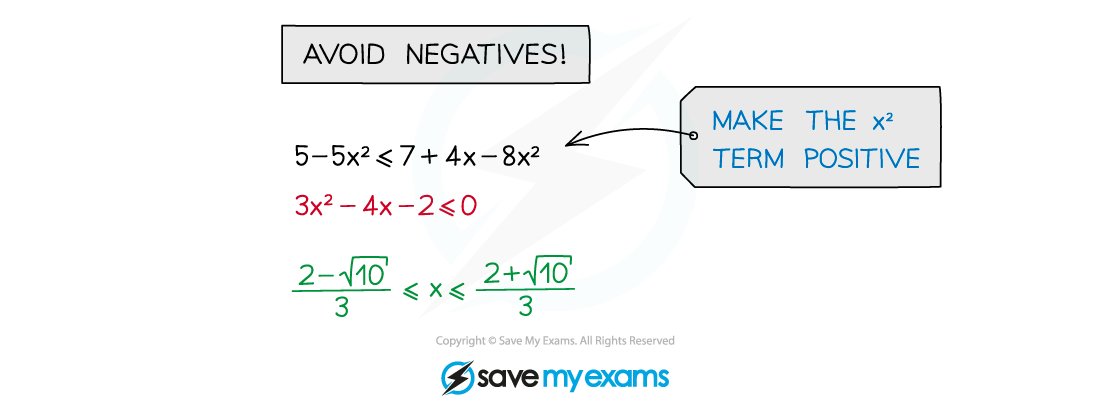
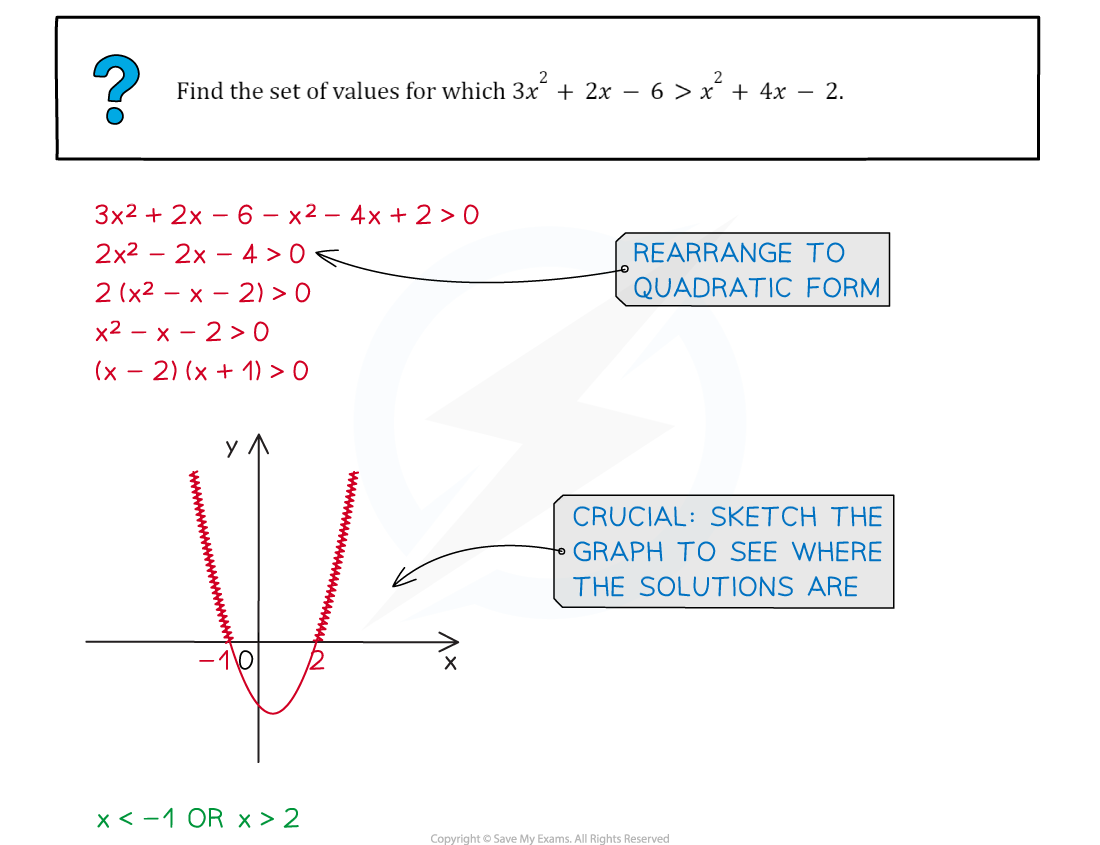
- STEP 1: Rearrange the inequality into quadratic form with a positive squared term
- ax2 + bx + c > 0 (>, <, ≤ or ≥)
- STEP 2: Find the roots of the quadratic equation
- Solve ax2 + bx + c = 0 to get x1 and x2 where x1 < x2
- STEP 3: Sketch a graph of the quadratic and label the roots
- As the squared term is positive it will be "U" shaped
- STEP 4: Identify the region that satisfies the inequality
- For ax2 + bx + c > 0 you want the region above the x-axis
- The solution is x < x1 or x > x2
- For ax2 + bx + c < 0 you want the region below the x-axis
- The solution is x > x1 and x < x2
- This is more commonly written as x1 < x < x2
- For ax2 + bx + c > 0 you want the region above the x-axis
- Be careful:
- avoid multiplying or dividing by a negative numberif unavoidable, “flip” the inequality sign so < → >, ≥ → ≤, etc
- avoid multiplying or dividing by a variable (x) that could be negative(multiplying or dividing by x2 guarantees positivity (unless x could be 0) but this can create extra, invalid solutions)
- do rearrange to make the x2 term positive
Worked Example
Exam Tip
- A calculator can be super-efficient but some marks are for method.
- Use your judgement:
- is it a “show that” or “prove” question?
- how many marks?
- how long is the question?
转载自savemyexams
国际竞赛真题资料-点击免费领取！
美高学分项目重磅来袭！立即了解
AMC8备考管家服务全新上线！
